Sphere of inner radius a and outer radius b is made of p uniform resistivity find resistance between inner and outer surface
p4π(1a−1b)
p2π(1a−1b)
p3π(2a−1b)
p2π(22a−1b)
The correct Answer is:A
To find the resistance between the inner and outer surfaces of a spherical shell with inner radius a, outer radius b, and uniform resistivity ρ, we can follow these steps:
Step 1: Understand the Geometry
We have a spherical shell with:
- Inner radius a
- Outer radius b
We need to find the resistance between the inner surface (radius a) and the outer surface (radius b).
Step 2: Consider a Thin Spherical Shell
Consider a thin spherical shell of radius r and thickness dr within the spherical shell. The resistance dR of this thin shell can be expressed as:
dR=ρdrA
where A is the surface area of the thin shell.
Step 3: Calculate the Surface Area
The surface area A of a sphere of radius r is given by:
A=4πr2
Step 4: Substitute the Surface Area into the Resistance Formula
Substituting A into the resistance formula gives:
dR=ρdr4πr2
Step 5: Integrate to Find Total Resistance
To find the total resistance R between the inner radius a and the outer radius b, we need to integrate dR from r=a to r=b:
R=∫badR=∫baρdr4πr2
Step 6: Perform the Integration
The integral can be computed as follows:
R=ρ4π∫badrr2
The integral ∫drr2 evaluates to −1r:
R=ρ4π(−1r)ba=ρ4π(−1b+1a)
This simplifies to:
R=ρ4π(1a−1b)
Step 7: Final Expression for Resistance
Thus, the resistance between the inner and outer surfaces of the spherical shell is:
R=ρ4π(1a−1b)
We have a spherical shell with:
- Inner radius a
- Outer radius b
Consider a thin spherical shell of radius r and thickness dr within the spherical shell. The resistance dR of this thin shell can be expressed as:
The surface area A of a sphere of radius r is given by:
Substituting A into the resistance formula gives:
To find the total resistance R between the inner radius a and the outer radius b, we need to integrate dR from r=a to r=b:
The integral can be computed as follows:
Thus, the resistance between the inner and outer surfaces of the spherical shell is:
Topper's Solved these Questions
Similar Questions
A hollow cylinder of specific resistance ρ, inner radius R, outer radius 2R and length l is as shown in figure. What is the net resistance between the inner and outer surfaces?
View SolutionA cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)
View Solution
Knowledge Check
A copper cylindrical tube has inner radius a and outer radius b. The resistivity is p. The resistance of . the cylinder between the two ends is
Aρlb2−a2Bρl2π(b−a)Cρlπ(b2−a2)Dπ(b2−a2)ρlSpace between tow concentric spheres of radii r1andr2 such that r1<r2 is filled with a material of resistivity ρ. Find the resistance between inner and outer surface of the material
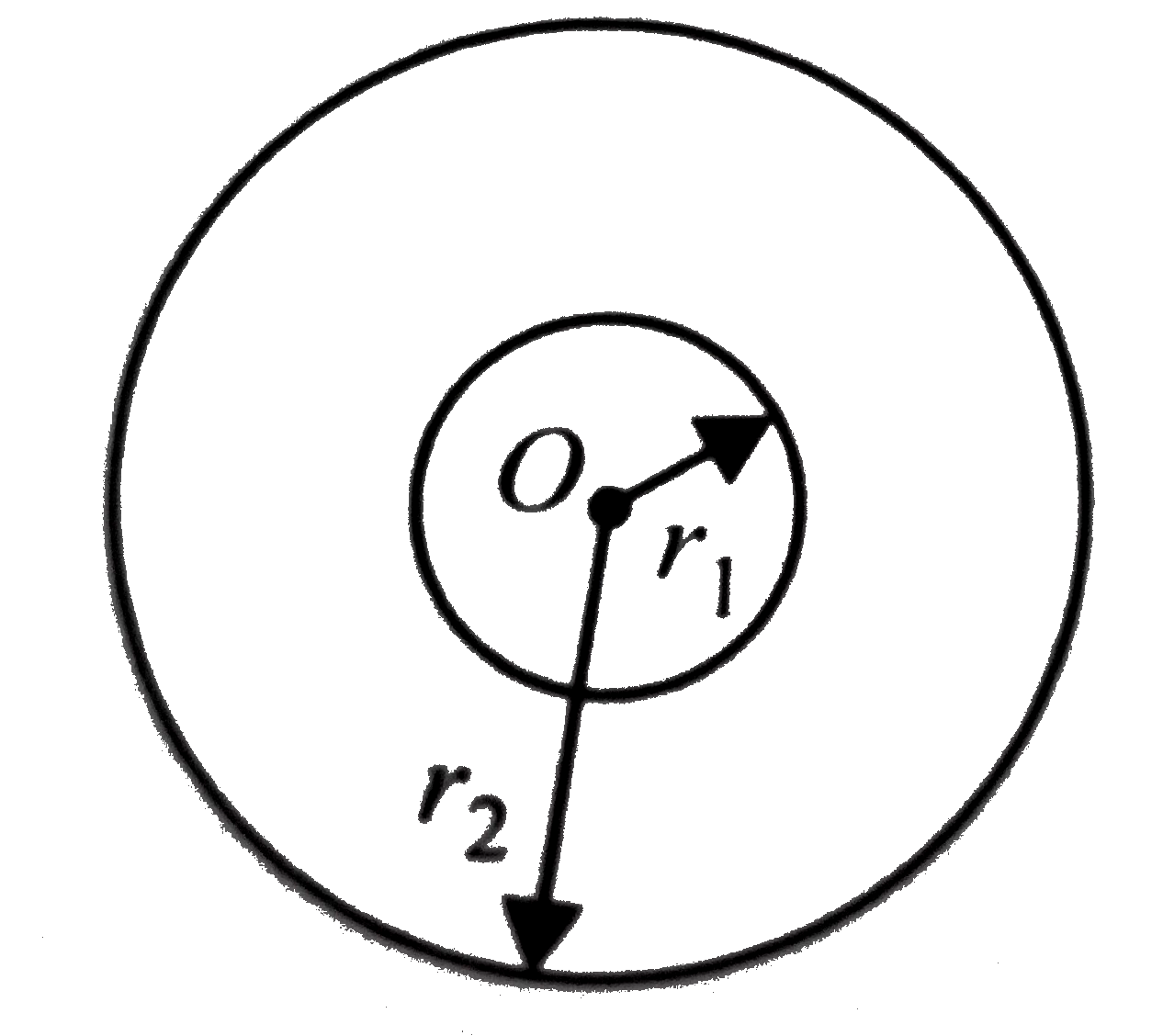 Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
Ar1r2p2Br2−r1r1r2p4πCr1r2r2−r1p4πDnone of these.
A point charge +q is placed at the centre of a conducting spherical shell of inner radius a and outer radius b. Find the charge appearing on the inner and outer surface of the shell.
View SolutionStatement-1 : A hollow metallic sphere of inner radius a and outer radius b has charge q at the centre. A negatively charged moves from inner surface outer surface. Then total work done will be zero.
Statement-2: Potential is constant inside the metallic sphere.
View SolutionA cylinderical tube of length L has inner radius a and outer radius b. What is the resistance of the tube between its inner and outer surface ? Given that the resistivity of its material is ρ.
View SolutionThe moment of inertia of hollow sphere (mass M) of inner radius R and outer radius 2R, having material of uniform density, about a diametric axis is
View SolutionAn empty thick conducting shell of inner radius a and outer radius b is shown in figure. If it is obseved that the inner face of the carries a uniform charge density −σ and the surface carries a uniform charge density .σ.

If a point charge qA is placed at the center of the shell, then choose the correct statement(s)
View SolutionA coaxial cable made up of two conductors. The inner conductor is solid and is of radius R1 and the outer conductor is hollow of inner radius R2 and outer radius R3. The space between the conductors is filled with air. The inner and outer conductors are carrying currents of equal magnitudes and in opposite directions. Then the variation of magnetic field with distance from the axis is best plotted as
View Solution
