Question

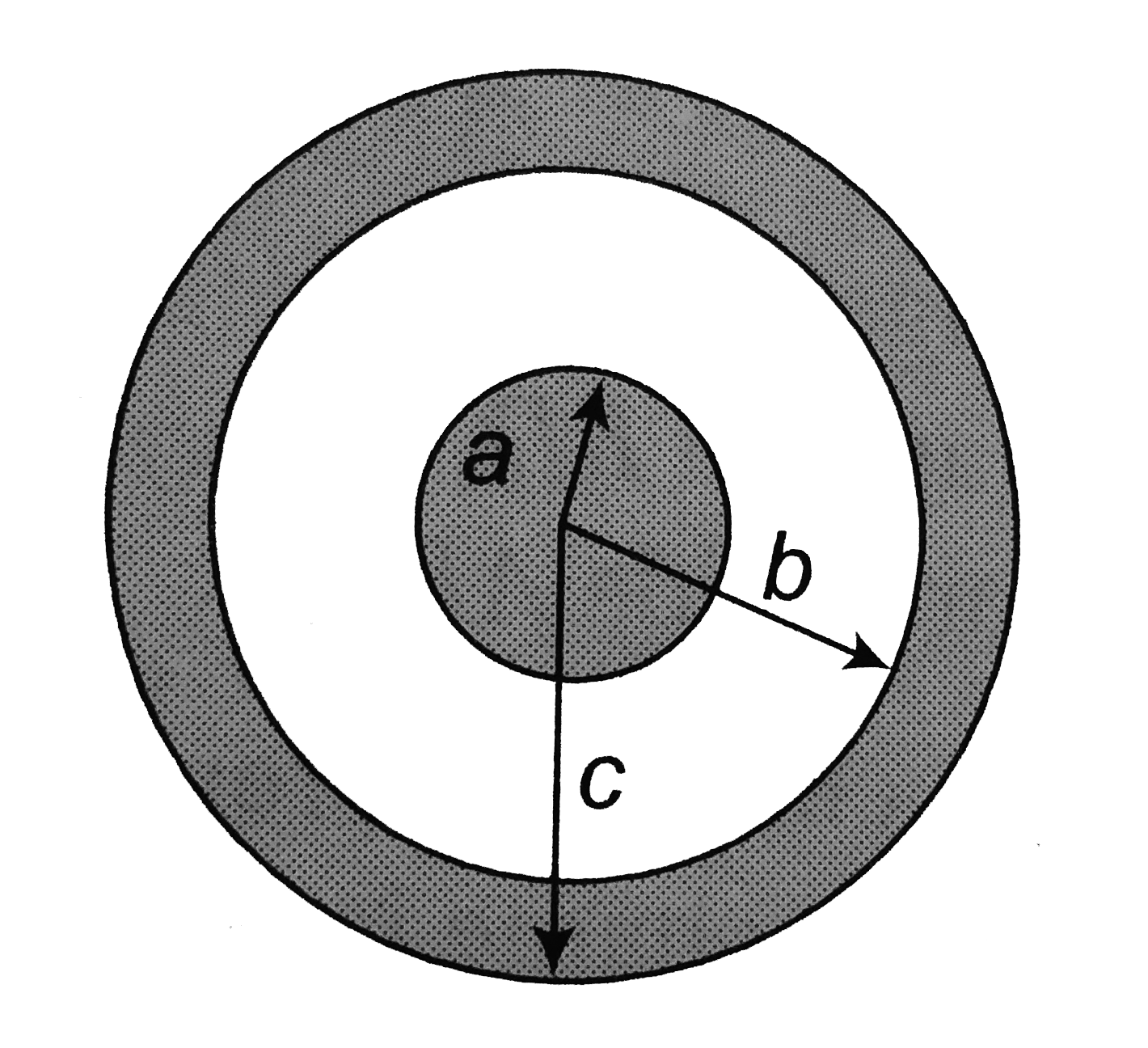
A cylindrical tube of length l has inner radius a while outer radius b. What is the resistance of the tube between (a) its ends (b) inner and outer surfaces ? (The resistivitiy of its material is p)

Explanation

To solve the problem, we need to find the resistance of a cylindrical tube in two different scenarios:

(a) Between its ends (along the length of the tube)
(b) Between its inner and outer surfaces (radially)

1. Identify the formula for resistance:
The resistance \( R \) of a conductor is given by the formula:
\( R = \frac{\rho L}{A} \)
where \( \rho \) is the resistivity of the material, \( L \) is the length of the conductor, and \( A \) is the cross-sectional area.

2. Calculate the cross-sectional area:
The tube has an inner radius \( a \) and an outer radius \( b \). The cross-sectional area \( A \) of the tube can be calculated by subtracting the area of the inner circle from the area of the outer circle:
\( A = \pi b^2 - \pi a^2 = \pi (b^2 - a^2) \)

3. Substitute the values into the resistance formula:
Now, substituting the values into the resistance formula:
\( R = \frac{\rho L}{\pi (b^2 - a^2)} \)

Thus, the resistance of the tube between its ends is:
\( R = \frac{\rho L}{\pi (b^2 - a^2)} \)

---

(b) Resistance between the inner and outer surfaces:

1. Consider a differential element:
To find the resistance between the inner and outer surfaces, consider a thin cylindrical shell of thickness \( dx \) at a radius \( x \) (where \( a < x < b \)).

2. Calculate the differential resistance \( dR \):
The resistance of this thin shell can be expressed as:
\( dR = \frac{\rho dx}{A} \)
where \( A \) is the surface area of the cylindrical shell, given by:
\( A = 2 \pi x L \)
Therefore, the differential resistance becomes:
\( dR = \frac{\rho dx}{2 \pi x L} \)

3. Integrate to find total resistance:
To find the total resistance \( R \) from the inner surface (radius \( a \)) to the outer surface (radius \( b \)), integrate \( dR \) from \( a \) to \( b \):
\( R = \int_a^b dR = \int_a^b \frac{\rho dx}{2 \pi x L} \)
This can be simplified as:
\( R = \frac{\rho}{2 \pi L} \int_a^b \frac{dx}{x} \)
The integral \( \int \frac{dx}{x} \) evaluates to \( \log x \), so we have:
\( R = \frac{\rho}{2 \pi L} (\log b - \log a) = \frac{\rho}{2 \pi L} \log \left( \frac{b}{a} \right) \)

Thus, the resistance of the tube between its inner and outer surfaces is:
\( R = \frac{\rho}{2 \pi L} \log \left( \frac{b}{a} \right) \)

Final Answers
- (a) Resistance between the ends:
\( R = \frac{\rho L}{\pi (b^2 - a^2)} \)
- (b) Resistance between the inner and outer surfaces:
\( R = \frac{\rho}{2 \pi L} \log \left( \frac{b}{a} \right) \)