A block of side 0.5m is 30% submerged in a liquid of density 1gm/(cc). Then find mass of an object placed on block for complete submergence.
87.3kg
85.3kg
82.3kg
80.3KG
The correct Answer is:A
To solve the problem step by step, we will analyze the forces acting on the block and use the principles of buoyancy.
Step 1: Understand the problem
We have a block with a side length of 0.5m that is 30% submerged in a liquid with a density of 1g/cm3. We need to find the mass of an object that must be placed on the block to make it completely submerged.
Step 2: Calculate the volume of the block
The volume V of a cube is given by:
V=side3=(0.5m)3=0.125m3
Step 3: Calculate the submerged volume of the block
Since the block is 30% submerged, the submerged volume Vs is:
Vs=0.3×V=0.3×0.125m3=0.0375m3
Step 4: Calculate the buoyant force acting on the block
The buoyant force Fb is equal to the weight of the liquid displaced by the submerged volume. The density of the liquid is 1g/cm3 which is equivalent to 1000kg/m3. Thus, the buoyant force can be calculated as:
Fb=density×Vs×g=1000kg/m3×0.0375m3×g
Fb=37.5kg⋅g
Step 5: Set up the equation for equilibrium
At equilibrium, the buoyant force equals the weight of the block plus the weight of the additional mass m placed on the block:
Fb=Mg+mg
Where M is the mass of the block. We can cancel g from both sides:
37.5=M+m
Step 6: Calculate the mass of the block
To find M, we need to calculate the mass of the block. The mass M can be calculated using the total volume and the density:
M=density×V=1000kg/m3×0.125m3=125kg
Step 7: Substitute M back into the equilibrium equation
Now substituting M into the equilibrium equation:
37.5=125+m
Rearranging gives:
m=37.5−125=−87.5kg
Step 8: Find the required mass for complete submergence
Since we need the block to be completely submerged, we can set up the equation again with the new total mass:
Fb=(M+m)g
We know that for complete submergence, the buoyant force must equal the total weight:
Fb=1000×V×g
Substituting V=0.125m3:
Fb=1000×0.125×g=125kg⋅g
Setting this equal to the total weight:
125=125+m
Solving for m:
m=125−125=0kg
Final Answer
The mass of the object that must be placed on the block for complete submergence is approximately 87.5kg.
---
We have a block with a side length of 0.5m that is 30% submerged in a liquid with a density of 1g/cm3. We need to find the mass of an object that must be placed on the block to make it completely submerged.
The volume V of a cube is given by:
V=side3=(0.5m)3=0.125m3
Since the block is 30% submerged, the submerged volume Vs is:
Vs=0.3×V=0.3×0.125m3=0.0375m3
The buoyant force Fb is equal to the weight of the liquid displaced by the submerged volume. The density of the liquid is 1g/cm3 which is equivalent to 1000kg/m3. Thus, the buoyant force can be calculated as:
Fb=density×Vs×g=1000kg/m3×0.0375m3×g
Fb=37.5kg⋅g
At equilibrium, the buoyant force equals the weight of the block plus the weight of the additional mass m placed on the block:
Fb=Mg+mg
Where M is the mass of the block. We can cancel g from both sides:
37.5=M+m
To find M, we need to calculate the mass of the block. The mass M can be calculated using the total volume and the density:
M=density×V=1000kg/m3×0.125m3=125kg
Now substituting M into the equilibrium equation:
37.5=125+m
Rearranging gives:
m=37.5−125=−87.5kg
Since we need the block to be completely submerged, we can set up the equation again with the new total mass:
Fb=(M+m)g
We know that for complete submergence, the buoyant force must equal the total weight:
Fb=1000×V×g
Substituting V=0.125m3:
Fb=1000×0.125×g=125kg⋅g
Setting this equal to the total weight:
125=125+m
Solving for m:
m=125−125=0kg
The mass of the object that must be placed on the block for complete submergence is approximately 87.5kg.
Topper's Solved these Questions
Similar Questions
_E01_052_Q01.png)
An object of volume V is submerged in a liquid of density ρ. It has flat bottom of area A which is at depth of H in the liquid and a dome shaped top find the total force of liquid acting on the top of the object.
View SolutionA small block of wood of density 0.4×103kg/m3 is submerged in water at a depth of 2.9m. Find
(a) the acceletation of the block towards the surface when the block is released and
(b) the time for the block to reach the surface, Ignore viscosity.
View SolutionA block of density 2000kg/m3 and mass 10kg is suspended by a spring stiffness 100N/m. The other end of the spring is attached to a fixed support. The block is completely submerged in a liquid of density 1000kg/m3. If the block is in equilibrium position.
View SolutionA block of iron has dimensions 2 m x 0.5 m x 0.25 m. The density of iron is 7.8gcm−3 . Find the mass of block.
View SolutionA wooden cube of side 10 cm and density 0.8 gm/cm3 is floating in water (density =1 gm/cm3). A mass of (100x) gm is placed over the cube so that cube is completely immersed without wetting the mass. Find value of x.
View SolutionA cubical block of side 0.5 M floats on water with 30% of its volume under water. What is the maximum weight that can be put on the block without fully submerging it under water?
[Take density of water =103kg/m3]
View SolutionTwo unequal blocks placed over each other of densities σ1 and σ2 are immersed in a fluid of density of σ. The block of density σ1 is fully submerged so that ratio of their masses is 12 and σ/σ1=2 and σ/σ2=0.5. Find the degree of submergence of the upper block of density σ2.
View SolutionA wooden cube (density 0.5 gm/c c) of side 10 cm floating in water kept in a cylindrical beaker of base area 1500cm2. When a mass m is kept on the wooden block the level of water rises in the beaker by 2mm. Find the mass m.
View SolutionA block of volume V and density σb is placed in liquid of density σ1(σ1>σb), then block is moved upward upto a height h and it is still in liquid. The increase in gravitational energy of the block is :
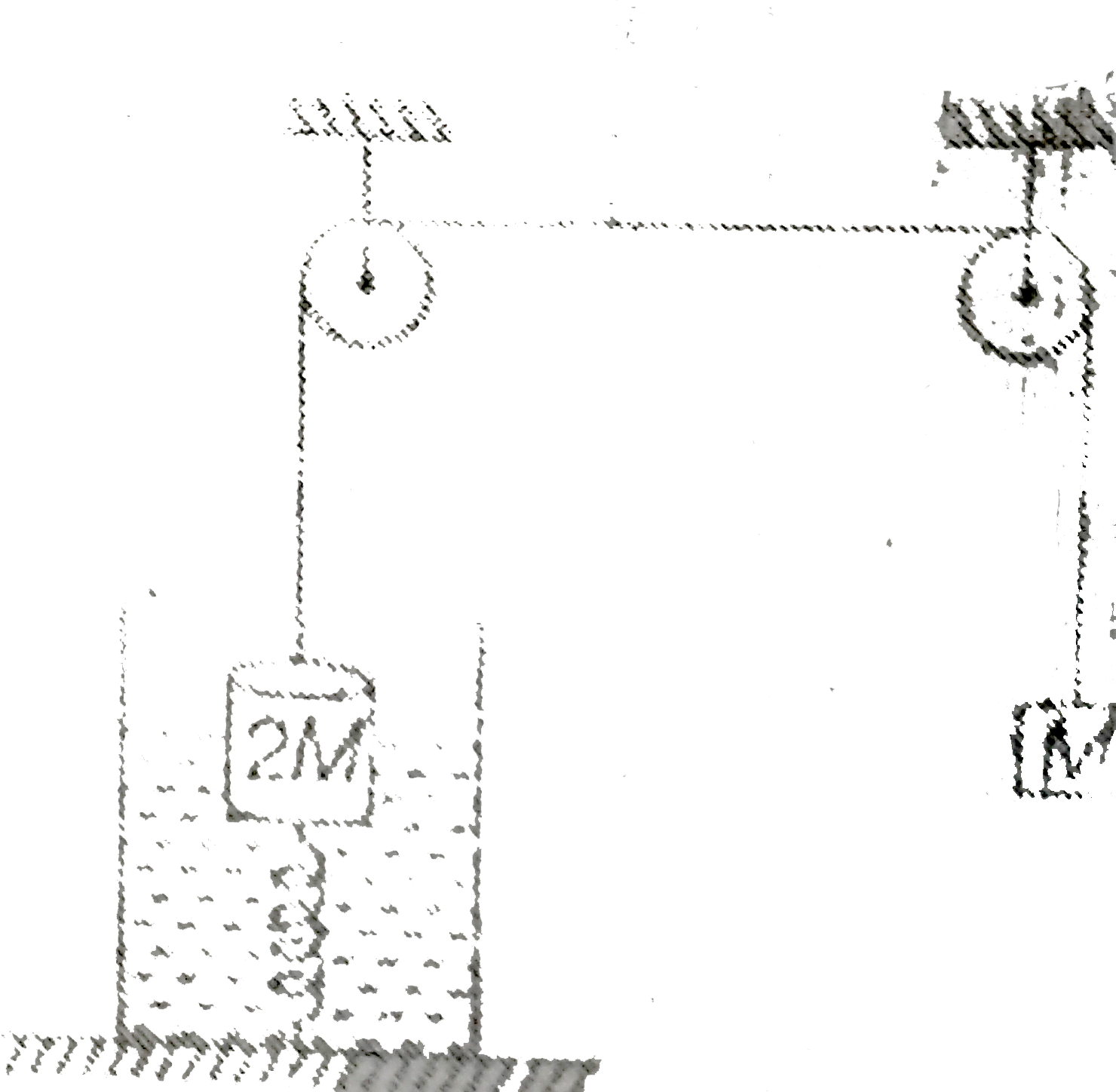
View SolutionPassage XIV) A uniform cylindrical block of mass 2M and cross-sectional area A remains partially submerged in a non viscous liquid of density ρ, density of the material of the cylinder is 3ρ. The cylinder is connected to lower end of the tank by means of a light spring of spring constant K. The other end of the cylinder is connected to anotehr block of mass M by means of a light inextensible sting as shown in the figure. The pulleys shown are massless and frictionless and assume that the cross-section of the cylinder is very small in comparison to that of the tank. Under equilibrium conditions, half of the cylinder is submerged. [given that cylinder always remains partially immersed)
Under equilibrium conditions
View Solution
