A dipole is placed at the origin such that its dipole moment is →p=−pˆi, The electric field and potential at (0,d,0) respectively are :
p4pε0d3ˆi,0
−p4pε0d3ˆi,0
2p4pε0d3ˆi,0
2p4pε0d3ˆi,0
The correct Answer is:D
To solve the problem, we need to find the electric field and potential at the point (0, d, 0) due to a dipole located at the origin with a dipole moment given by →p=−p^i.
1. Understanding the Dipole Configuration:
- A dipole consists of two equal and opposite charges separated by a small distance. The dipole moment →p is directed from the negative charge to the positive charge.
- Here, the dipole moment is given as →p=−p^i, which means the positive charge is located at (−d/2,0,0) and the negative charge at (d/2,0,0) along the x-axis.
2. Identifying the Point of Interest:
- We need to calculate the electric field and potential at the point (0, d, 0), which lies on the y-axis.
3. Calculating the Electric Potential:
- The electric potential V due to a dipole at a point in space is given by the formula:
V=→p⋅^r4πϵ0r2
- Here, ^r is the unit vector from the dipole to the point of interest, and r is the distance from the dipole to that point.
- The distance r from the origin (dipole) to the point (0, d, 0) is:
r=√02+d2+02=d
- The unit vector ^r is:
^r=(0,d,0)d=(0,1,0)=^j
- Now substituting into the potential formula:
V=−p^i⋅^j4πϵ0d2=0
- Since ^i⋅^j=0, the electric potential V at the point (0, d, 0) is zero.
4. Calculating the Electric Field:
- The electric field →E due to a dipole at a point along the axial line (the line extending through both charges) is given by:
→E=14πϵ0⋅2→pr3
- Since the point (0, d, 0) is not on the axial line of the dipole, we use the general formula for the electric field due to a dipole:
→E=14πϵ0⋅1r3(3(→p⋅^r)^r−→p)
- Substituting →p=−p^i and ^r=^j:
→E=14πϵ0⋅1d3(3(−p^i⋅^j)^j−(−p^i))
- Since ^i⋅^j=0:
→E=14πϵ0⋅pd3^i
5. Final Results:
- The electric potential at the point (0, d, 0) is:
V=0
- The electric field at the point (0, d, 0) is:
→E=p4πϵ0d3^i
Summary:
- Electric Potential V=0
- Electric Field →E=p4πϵ0d3^i
- A dipole consists of two equal and opposite charges separated by a small distance. The dipole moment →p is directed from the negative charge to the positive charge.
- Here, the dipole moment is given as →p=−p^i, which means the positive charge is located at (−d/2,0,0) and the negative charge at (d/2,0,0) along the x-axis.
- We need to calculate the electric field and potential at the point (0, d, 0), which lies on the y-axis.
- The electric potential V due to a dipole at a point in space is given by the formula:
V=→p⋅^r4πϵ0r2
- Here, ^r is the unit vector from the dipole to the point of interest, and r is the distance from the dipole to that point.
- The distance r from the origin (dipole) to the point (0, d, 0) is:
r=√02+d2+02=d
- The unit vector ^r is:
^r=(0,d,0)d=(0,1,0)=^j
- Now substituting into the potential formula:
V=−p^i⋅^j4πϵ0d2=0
- Since ^i⋅^j=0, the electric potential V at the point (0, d, 0) is zero.
- The electric field →E due to a dipole at a point along the axial line (the line extending through both charges) is given by:
→E=14πϵ0⋅2→pr3
- Since the point (0, d, 0) is not on the axial line of the dipole, we use the general formula for the electric field due to a dipole:
→E=14πϵ0⋅1r3(3(→p⋅^r)^r−→p)
- Substituting →p=−p^i and ^r=^j:
→E=14πϵ0⋅1d3(3(−p^i⋅^j)^j−(−p^i))
- Since ^i⋅^j=0:
→E=14πϵ0⋅pd3^i
- The electric potential at the point (0, d, 0) is:
V=0
- The electric field at the point (0, d, 0) is:
→E=p4πϵ0d3^i
- Electric Potential V=0
- Electric Field →E=p4πϵ0d3^i
Topper's Solved these Questions
Similar Questions
A small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View SolutionA short magnetic dipole when placed at origin with its dipole moment oriented along x-axis , the magnetic field at the point (a,0) is →B . What will be the magnetic field at the above point , if another identical dipole is also placed at origin with its dipole moment oriented along y-axis ?
View SolutionA dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
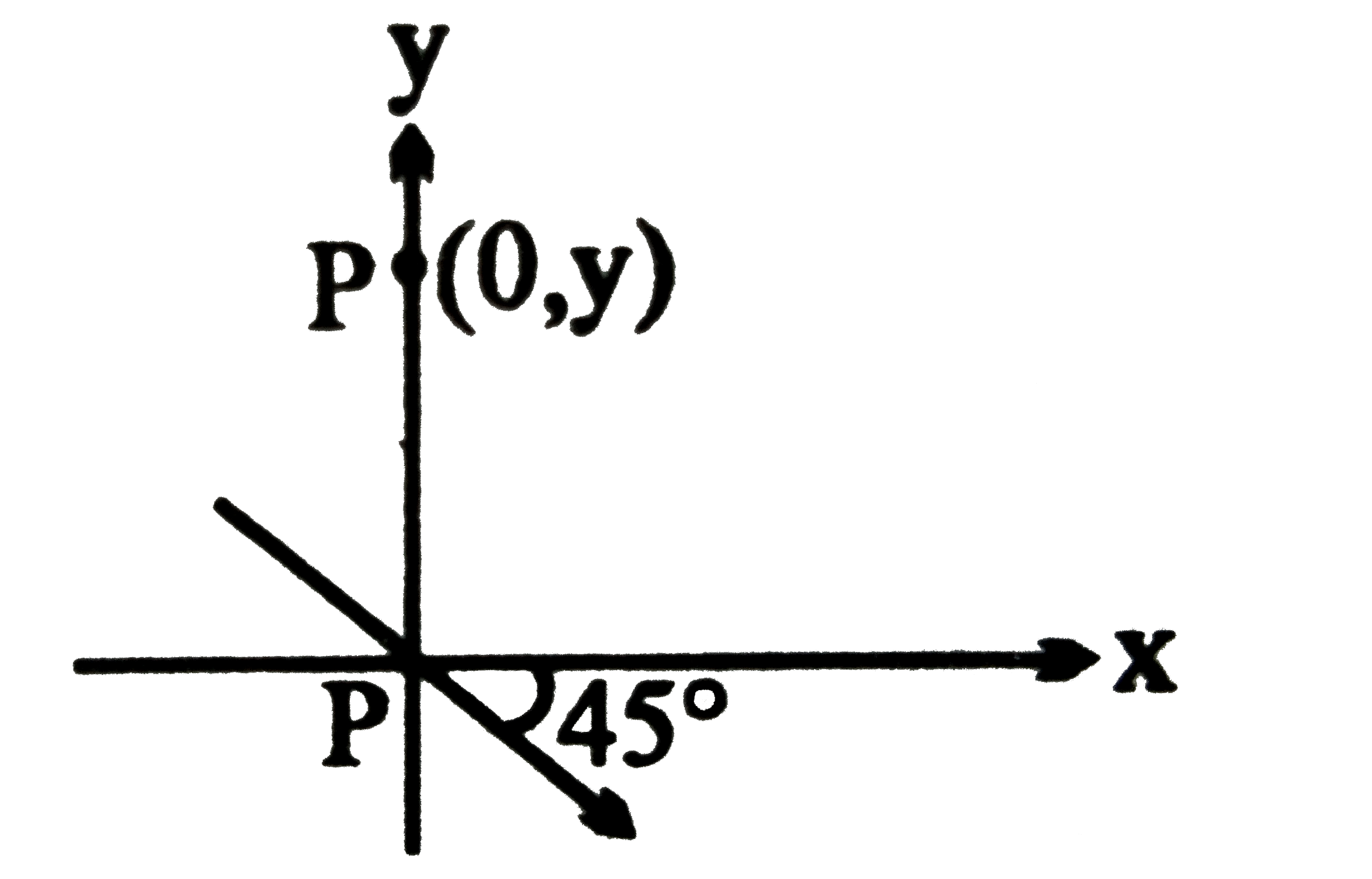 .
.
View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole is placed at the origin O and is directed along the x-axis. At a point P, far away from the dipole, the electric field is parallel to y-axis. OP makes an angle θ with the x-axis then
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
(a) 2qE and minimum (b) qE and pE
(c) zero and minimum (d) qE and maximum
View SolutionTwo short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by
View SolutionA point dipole →p=−p0xˆx is kept at the origin. The potential and electric field due to this dipole on the y-axis at a distance d are respectively (take V=0 at infinity)
View SolutionAn electric dipole has the magnitude of its charge as q and its dipole moment is p. It is placed in a uniform electric field E. If its dipole moment is along the direction of the field, the force on it and its potential energy are respectively
View Solution
