Two short dipoles, each of diple moment p , are placed at origin. The dipole moment of one dipole is along x-axis, while that of other is along y-axis . The electric field at a point (a,0) is given by
(14πε0)2pa3
(14πε0)pa3
(14πε0)√5pa3
Zero
The correct Answer is:3
To find the electric field at the point (a, 0) due to two dipoles placed at the origin, we will follow these steps:
Step 1: Understanding the Dipoles
We have two dipoles, each with a dipole moment →p. One dipole is oriented along the x-axis, and the other is oriented along the y-axis.
Step 2: Electric Field Due to the Dipole Along the X-axis
The electric field →Ex at a point due to a dipole along the x-axis at a distance r is given by:
→Ex=2kpr3^i
where k is the Coulomb's constant, p is the dipole moment, and ^i is the unit vector in the x-direction.
At the point (a, 0), the distance r is a, so:
→Ex=2kpa3^i
Step 3: Electric Field Due to the Dipole Along the Y-axis
The electric field →Ey at the same point (a, 0) due to the dipole along the y-axis is given by:
→Ey=−kpr3^j
Here, the electric field is directed opposite to the dipole moment because the point (a, 0) is at the equatorial position of the dipole along the y-axis.
Again, substituting r=a:
→Ey=−kpa3^j
Step 4: Net Electric Field
The net electric field →Enet at the point (a, 0) is the vector sum of →Ex and →Ey:
→Enet=→Ex+→Ey=2kpa3^i−kpa3^j
Step 5: Simplifying the Expression
We can factor out kpa3:
→Enet=kpa3(2^i−^j)
Step 6: Magnitude of the Electric Field
To find the magnitude of the electric field:
|→Enet|=kpa3√(2)2+(−1)2=kpa3√4+1=kpa3√5
Step 7: Final Expression
Substituting k with 14πϵ0:
|→Enet|=14πϵ0⋅√5pa3
Thus, the electric field at the point (a, 0) is given by:
→Enet=14πϵ0⋅√5pa3^r
where ^r is the direction of the resultant electric field.
We have two dipoles, each with a dipole moment →p. One dipole is oriented along the x-axis, and the other is oriented along the y-axis.
The electric field →Ex at a point due to a dipole along the x-axis at a distance r is given by:
→Ex=2kpr3^i
where k is the Coulomb's constant, p is the dipole moment, and ^i is the unit vector in the x-direction.
→Ex=2kpa3^i
The electric field →Ey at the same point (a, 0) due to the dipole along the y-axis is given by:
→Ey=−kpr3^j
Here, the electric field is directed opposite to the dipole moment because the point (a, 0) is at the equatorial position of the dipole along the y-axis.
→Ey=−kpa3^j
The net electric field →Enet at the point (a, 0) is the vector sum of →Ex and →Ey:
→Enet=→Ex+→Ey=2kpa3^i−kpa3^j
We can factor out kpa3:
→Enet=kpa3(2^i−^j)
To find the magnitude of the electric field:
|→Enet|=kpa3√(2)2+(−1)2=kpa3√4+1=kpa3√5
Substituting k with 14πϵ0:
|→Enet|=14πϵ0⋅√5pa3
→Enet=14πϵ0⋅√5pa3^r
where ^r is the direction of the resultant electric field.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS (More than one answer))
13 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-D(COMPREHENSION-I)
2 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Four short dipoles each of dipole moment 'p' are placed at the vertices of a square of side a. The direction of the dipole moments are shown in the figure.

View SolutionA short magnetic dipole when placed at origin with its dipole moment oriented along x-axis , the magnetic field at the point (a,0) is →B . What will be the magnetic field at the above point , if another identical dipole is also placed at origin with its dipole moment oriented along y-axis ?
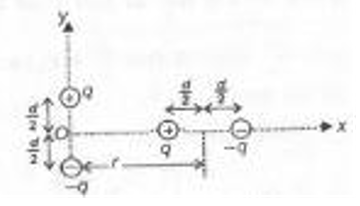
View SolutionTwo identical electric dipoles of dipole moments p are placed as shown in the figure. The electrostatic force on dipole placed along x-axis is (d << r) (14πε0 )
View SolutionWhat is the force on a dipole of dipole moment p placed as shown in fig.

View SolutionA small electric dipole is placed at origin with its dipole moment directed along positive x-axis .The direction of electric field at point (2,2√2,0)
View Solution4 charges are placed each at a distance a from origin . The dipole moment of configuration is .
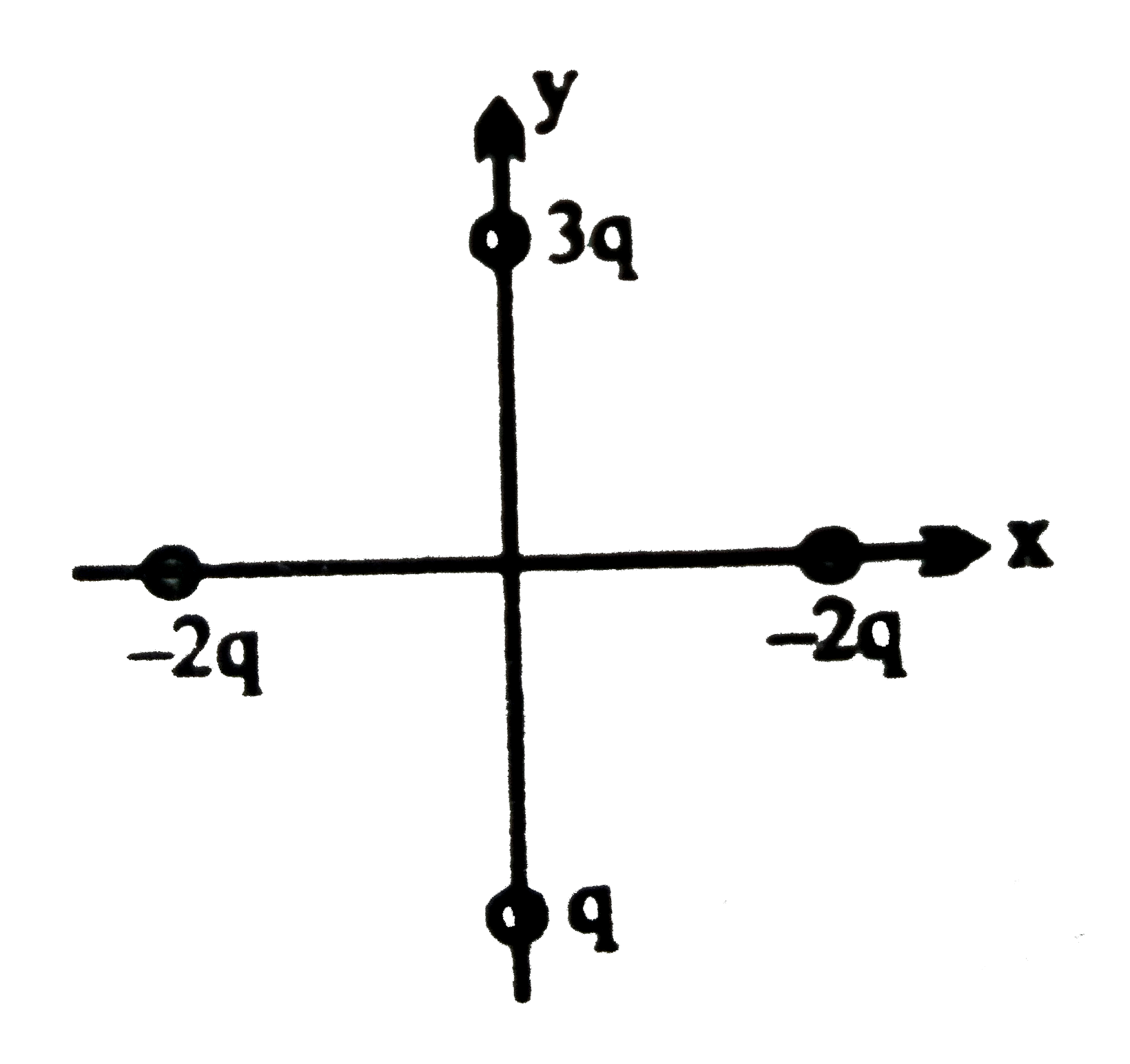 .
.
View Solutionfour charges are placed each at a distance from origin. the dipole moment of configuration is

View SolutionAn electric dipole is placed along x-axis with its centre at origin:
View SolutionTwo short electric dipoles are placed as shown. The energy of electric interaction these dipoles will be
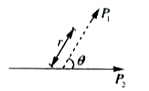
View SolutionA dipole is placed at origin of coordinate system as shown in figure, find the electric field at point P(0,y)
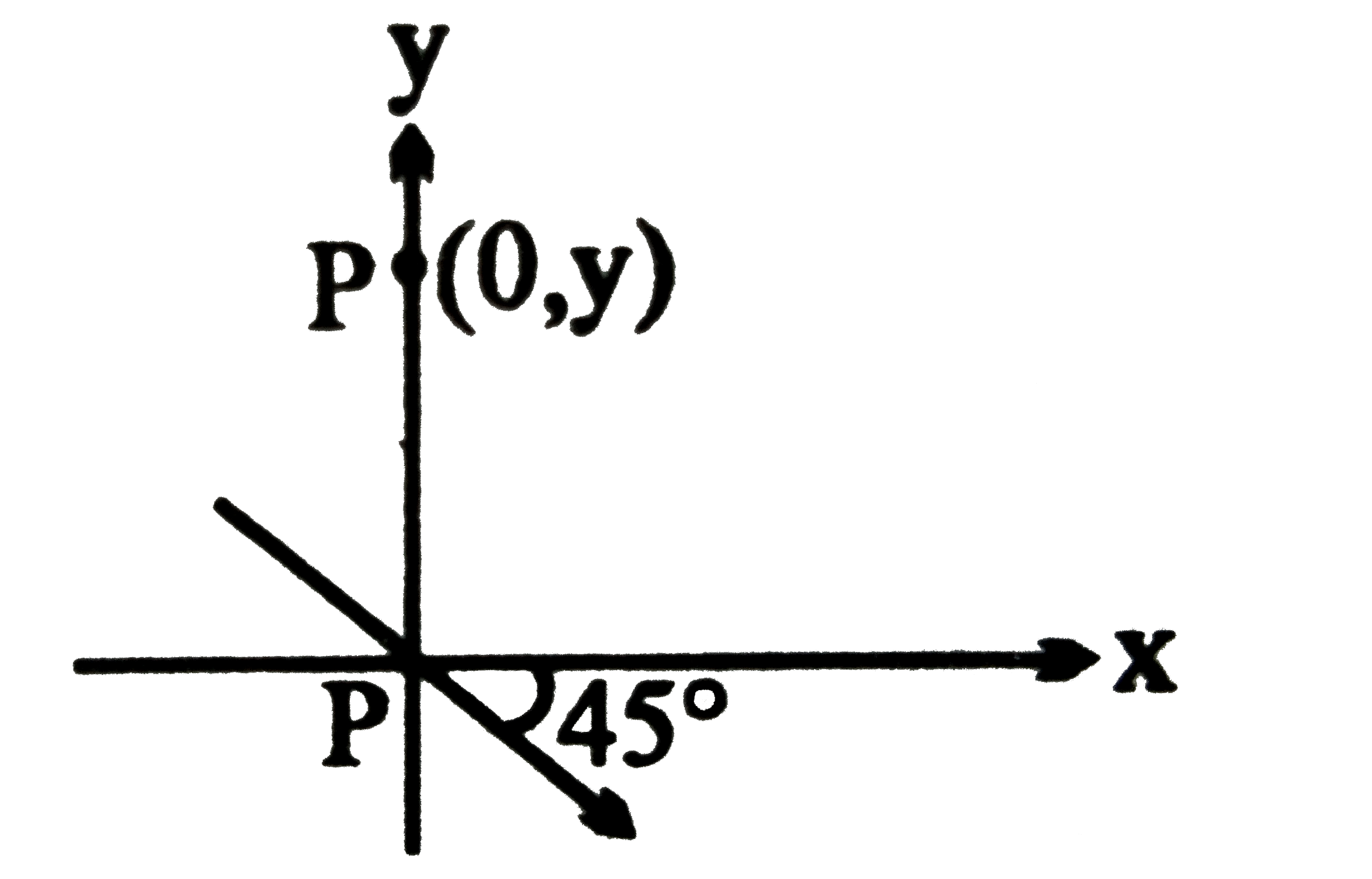 .
.
View Solution
