A long straight wire is placed along the axis of a circuit ring of radius R. The mutual inductance of this system is
μ0R2
μ0πR2
μ02
0
The correct Answer is:D
To find the mutual inductance of a long straight wire placed along the axis of a circular ring of radius R, we can follow these steps:
1. Understanding the Setup:
We have a long straight wire placed along the axis of a circular ring (loop) with radius R. The wire carries a current I.
2. Magnetic Field Due to the Wire:
The magnetic field (B) produced by a long straight wire at a distance r from it is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
3. Magnetic Flux Through the Ring:
The magnetic flux (Φ) through the circular ring due to the magnetic field from the wire can be calculated. The area (A) of the ring is given by:
A=πR2
The magnetic field is perpendicular to the area vector of the ring. Therefore, the magnetic flux is:
Φ=B⋅A=B⋅πR2
4. Substituting the Magnetic Field:
Substitute the expression for B into the flux equation:
Φ=(μ0I2πR)⋅πR2=μ0IR2
5. Calculating Mutual Inductance (M):
The mutual inductance (M) is defined as the ratio of the magnetic flux through the ring to the current in the wire:
M=ΦI=μ0IR2I=μ0R2
6. Conclusion:
Therefore, the mutual inductance of the system is:
M=μ0R2
Final Answer:
The mutual inductance of the system is M=μ0R2.
---
We have a long straight wire placed along the axis of a circular ring (loop) with radius R. The wire carries a current I.
The magnetic field (B) produced by a long straight wire at a distance r from it is given by the formula:
B=μ0I2πr
where μ0 is the permeability of free space.
The magnetic flux (Φ) through the circular ring due to the magnetic field from the wire can be calculated. The area (A) of the ring is given by:
A=πR2
The magnetic field is perpendicular to the area vector of the ring. Therefore, the magnetic flux is:
Φ=B⋅A=B⋅πR2
Substitute the expression for B into the flux equation:
Φ=(μ0I2πR)⋅πR2=μ0IR2
The mutual inductance (M) is defined as the ratio of the magnetic flux through the ring to the current in the wire:
M=ΦI=μ0IR2I=μ0R2
Therefore, the mutual inductance of the system is:
M=μ0R2
The mutual inductance of the system is M=μ0R2.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 1
14 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-2 PART 2
17 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - RESONANCE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Exercis-1
63 Videos
- ELECTRODYNAMICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTRODYNAMICSEXERCISE - Advanced level problems
31 Videos
- ELECTROSTATICSBOOK - RESONANCE ENGLISHCHAPTER - ELECTROSTATICSEXERCISE - HLP
40 Videos
Similar Questions
A very long uniformly charged wire oriented along the axis of a circular ring of radius R rests on its centre with one of the ends (as shown in figure). The linear charge density on the wire is λ. Evalute the flux of the vector →E across the circle area.

View SolutionA rectangular loop of sides 'a' and 'b' is placed in xy plane. A very long wire is also placed in xy plane such that side of length 'a' of the loop is parallel to the wire. The distance between the wire and the nearest edge of the loop is 'd'. The mutual inductance of this system is proportional to :
View SolutionA current- carrying straight wire is kept along the axis of a circular loop carrying a current. The straight wire
View SolutionA long, straight wire carries a current along the z-axis. One can find two points in the x-y plane such that
View SolutionThe figure shows a long straigh wire carryhing a current I1 along the axis of a circular ring carrying a current I_2. Identify the correct statement.

View SolutionA small square loop of wire of side l is placed inside a large square loop of wire of side L(L>>l). The loops are co-planer and their centres coincide. The mutual inductance of the system is proportional to
View SolutionA straight wire carrying an electric current is placed
along the axis of a uniformly charged ring. Will there
be a magnetic force on the wire if the ring starts rotating
about the wire? If yes, in which direction?
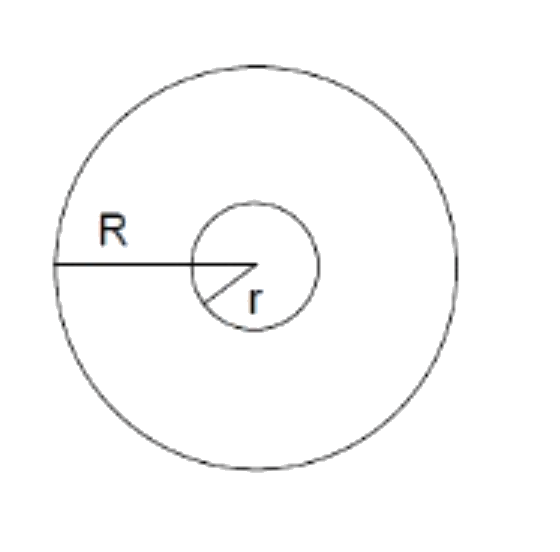
View SolutionTwo concentric co - planar circular loops of radius R and r(<<R) are placed as shown in the figure. The mutual inductance of the system will be
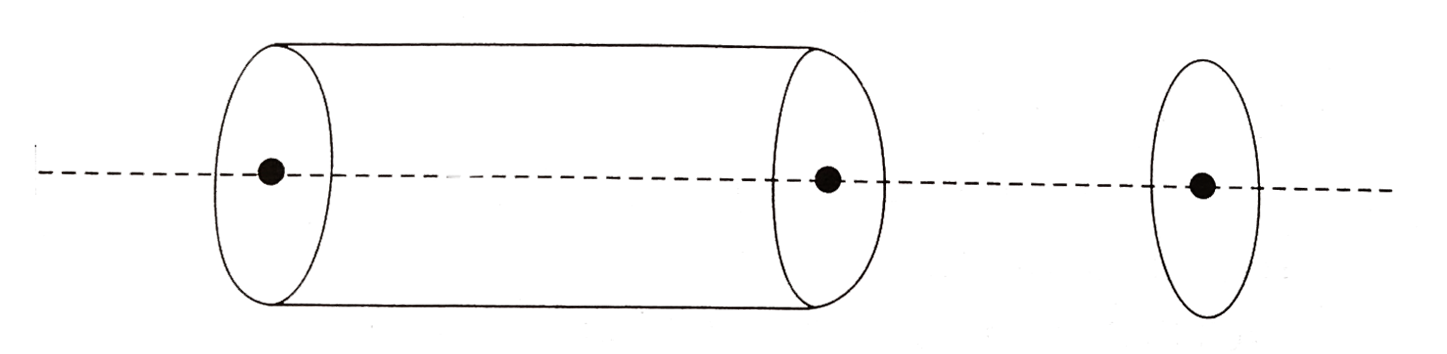
View SolutionThe diagram given below shows a solenoid carrying time varying current l=l0t. On the axis of the solenoid, a ring has been placed. The mutual inductance of the ring and the solenoid is M and the self inductance of the ring is L. If the resistance of the ring is R then maximum current which can flow through the ring is
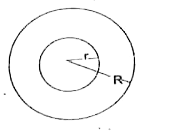
View SolutionThere is a the system of two concentric loops of radii r and R (R>>r) . Find the mutual inductance of the system . If the loops have currents of same magnitude i0 lgnore the effect of self inductance .
View Solution
