A uniform cable of mass 'M' and length 'L' is placed on a horizontal surface such that its (1n)th part is hanging below the edge of the cable upto the surface, the work done should be :
MgL2n2
MgLn2
2MgLn2
nMgL
The correct Answer is:C
To solve the problem, we need to determine the work done to lift the hanging part of a uniform cable back onto a horizontal surface. Let's break down the solution step by step.
1. Identify the Length and Mass of the Hanging Part:
- The total length of the cable is L.
- The fraction of the cable that is hanging is 1n, so the length of the hanging part is:
Lh=Ln
2. Calculate the Mass of the Hanging Part:
- The mass of the entire cable is M.
- The mass per unit length of the cable is:
mass per unit length=ML
- Therefore, the mass of the hanging part is:
mh=ML⋅Lh=ML⋅Ln=Mn
3. Determine the Center of Mass of the Hanging Part:
- The center of mass of the hanging part, which is a uniform cable, is located at half of its length from the top of the hanging part. Thus, the height of the center of mass from the table is:
h=Lh2=12⋅Ln=L2n
4. Calculate the Initial Potential Energy of the Hanging Part:
- The potential energy U of the hanging part when it is at height −h (below the reference level) is given by:
Ui=−mh⋅g⋅h=−(Mn)⋅g⋅(−L2n)=MgL2n2
5. Final Potential Energy:
- When the entire cable is on the table, the potential energy Uf is zero since it is at the reference level:
Uf=0
6. Calculate the Work Done:
- The work done W to lift the hanging part back onto the table is equal to the change in potential energy:
W=Uf−Ui=0−MgL2n2=−(−MgL2n2)=MgL2n2
Final Answer:
The work done to lift the hanging part of the cable back onto the table is:
W=MgL2n2
- The total length of the cable is L.
- The fraction of the cable that is hanging is 1n, so the length of the hanging part is:
Lh=Ln
- The mass of the entire cable is M.
- The mass per unit length of the cable is:
mass per unit length=ML
- Therefore, the mass of the hanging part is:
mh=ML⋅Lh=ML⋅Ln=Mn
- The center of mass of the hanging part, which is a uniform cable, is located at half of its length from the top of the hanging part. Thus, the height of the center of mass from the table is:
h=Lh2=12⋅Ln=L2n
- The potential energy U of the hanging part when it is at height −h (below the reference level) is given by:
Ui=−mh⋅g⋅h=−(Mn)⋅g⋅(−L2n)=MgL2n2
- When the entire cable is on the table, the potential energy Uf is zero since it is at the reference level:
Uf=0
- The work done W to lift the hanging part back onto the table is equal to the change in potential energy:
W=Uf−Ui=0−MgL2n2=−(−MgL2n2)=MgL2n2
The work done to lift the hanging part of the cable back onto the table is:
W=MgL2n2
Topper's Solved these Questions
Similar Questions
A uniform chain of mass M and length L is lying on a frictionless table in such a way that its 1/3 parts is hanging vertically down. The work done in pulling the chain up the table is
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View Solution
Knowledge Check
A chain of uniform mass m and length L is held on a frictionless table in such a way that its 1nth part is hanging below the edge of table. The work done to pull the hanging part of chain is :−
A√nBnCn−3Dn−2
A uniform chain of mass 4 kg and length 2 m is kept on table such that 3/10th of the chain hanges freely from the edge of the table. How much work has to be done in pulling the entire chain on the table?
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View SolutionA chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
View SolutionA uniform chain of mass m & length L is kept on a smooth horizontal table such that Lnportion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If a gentle push is given to hanging end, it will start moving down. What is the change in gravitational potential energy of the chain, as it just leaves the table?
View SolutionA uniform chain has a mass M and length L. It is placed on a frictionless table with length l0 hanging over the edge. The chain begins to slide down. Ten, the speed v with which the end slides down from the edge is given by
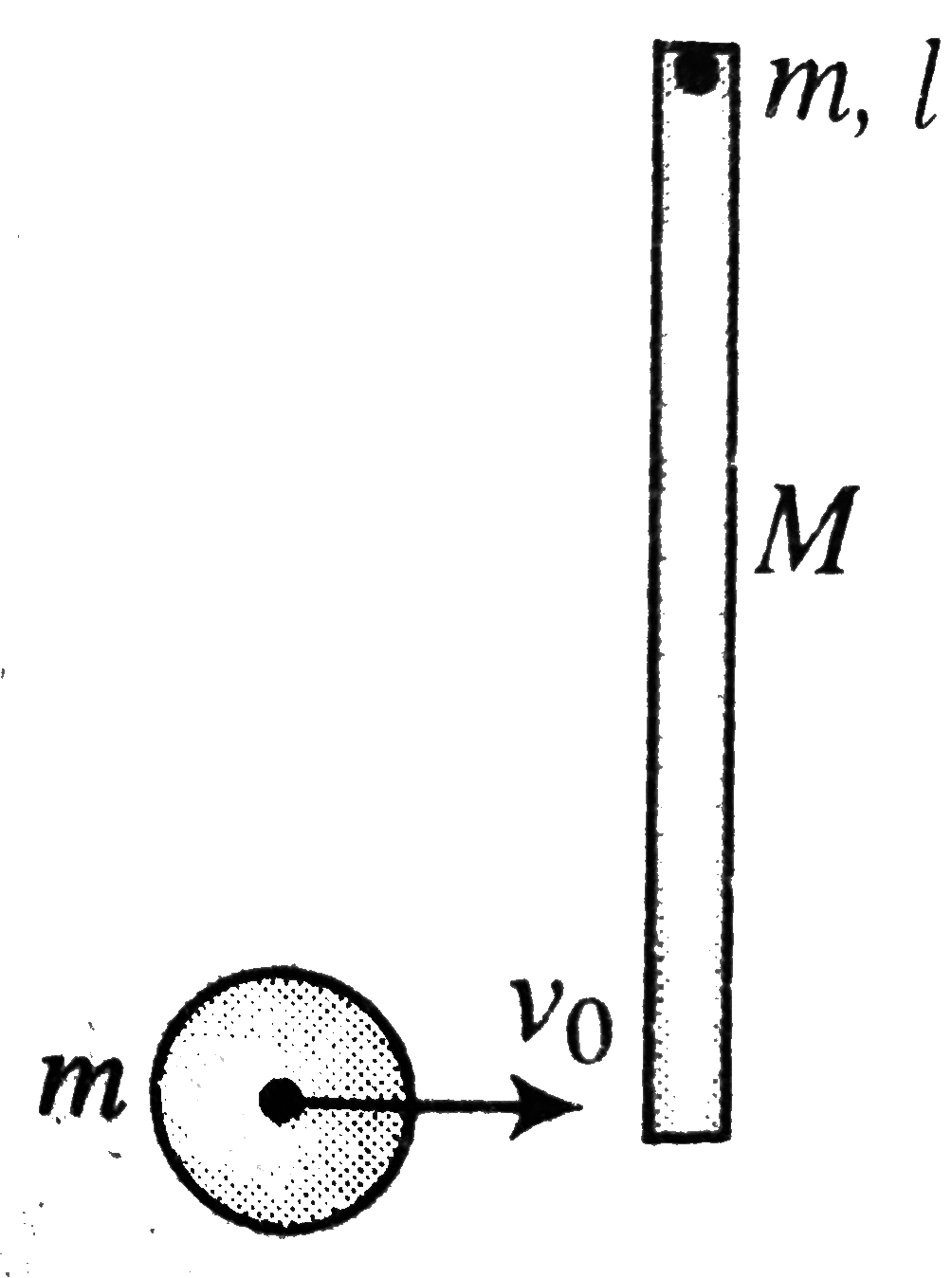
View SolutionA uniform rod of mass M and length l is placed on a smooth- horizontal surface with its one end pivoted to the surface. A small ball of mass m moving along the surface with a velocity v0, perpendicular to the rod, collides elastically with the free end of the rod. Find:
a. the angular velocity of the rod after collision.
b. the impulse applied by the pivot on the rod during collision. (Take M/m=2)
View Solution
