A chain of mass m and length L is held at rest on smooth horizontal surface such that a part I of the chain is hanging vertically from the table. If the chain is let go, what is its speed as its end just leaves the horizontal surface?
A. √g(L2−I22L)
B. √2g(L−I2L)
C. √g(L−I2L)
D. √gI2L
To solve the problem of finding the speed of the chain as its end just leaves the horizontal surface, we can follow these steps:
Step 1: Understand the System
We have a chain of mass m and length L resting on a smooth horizontal surface, with a part i of the chain hanging vertically. When the chain is released, the hanging part will fall due to gravity.
Step 2: Identify the Potential Energy
The potential energy (PE) of the hanging part of the chain can be calculated. The mass of the hanging part is given by:
mi=mL⋅i
where mi is the mass of the hanging part of the chain.
The potential energy of the hanging part when it is at height i is:
PE=mi⋅g⋅i=(mL⋅i)⋅g⋅i=mgi2L
Step 3: Use Conservation of Energy
When the chain is released, the potential energy will convert into kinetic energy (KE) as the chain falls. The kinetic energy of the chain when the end just leaves the surface is:
KE=12mv2
where v is the speed of the chain at that moment.
According to the principle of conservation of energy:
PEinitial=KEfinal
Thus, we have:
mgi2L=12mv2
Step 4: Simplify the Equation
We can cancel m from both sides (assuming m≠0):
gi2L=12v2
Now, multiply both sides by 2:
2gi2L=v2
Step 5: Solve for v
Taking the square root of both sides gives us the speed v:
v=√2gi2L
Step 6: Conclusion
This is the speed of the chain as its end just leaves the horizontal surface.
We have a chain of mass m and length L resting on a smooth horizontal surface, with a part i of the chain hanging vertically. When the chain is released, the hanging part will fall due to gravity.
The potential energy (PE) of the hanging part of the chain can be calculated. The mass of the hanging part is given by:
mi=mL⋅i
where mi is the mass of the hanging part of the chain.
PE=mi⋅g⋅i=(mL⋅i)⋅g⋅i=mgi2L
When the chain is released, the potential energy will convert into kinetic energy (KE) as the chain falls. The kinetic energy of the chain when the end just leaves the surface is:
KE=12mv2
where v is the speed of the chain at that moment.
PEinitial=KEfinal
Thus, we have:
mgi2L=12mv2
We can cancel m from both sides (assuming m≠0):
gi2L=12v2
Now, multiply both sides by 2:
2gi2L=v2
Taking the square root of both sides gives us the speed v:
v=√2gi2L
This is the speed of the chain as its end just leaves the horizontal surface.
Similar Questions
A uniform chain of mass m & length L is kept on a smooth horizontal table such that Lnportion of the chaing hangs from the table. The work dione required to slowly bringsthe chain completely on the table is
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

If the chain is limiting equlibrium, what is the coefficient of friction for the contact between table and chain?
View Solution
Knowledge Check
A chain of uniform mass m and length L is held on a frictionless table in such a way that its 1nth part is hanging below the edge of table. The work done to pull the hanging part of chain is :−
A√nBnCn−3Dn−2
A uniform cable of mass 'M' and length 'L' is placed on a horizontal surface such that its (1n)th part is hanging below the edge of the cable upto the surface, the work done should be :
View SolutionA uniform chain of mass m and length l is lying on a horizontal table with one-third of its length hanging over the edge of the table.

What is the speed of the chain, when it just loses contact with the table?
View SolutionA uniform chain of mass M and length L is lying on a frictionless table in such a way that its 1/3 parts is hanging vertically down. The work done in pulling the chain up the table is
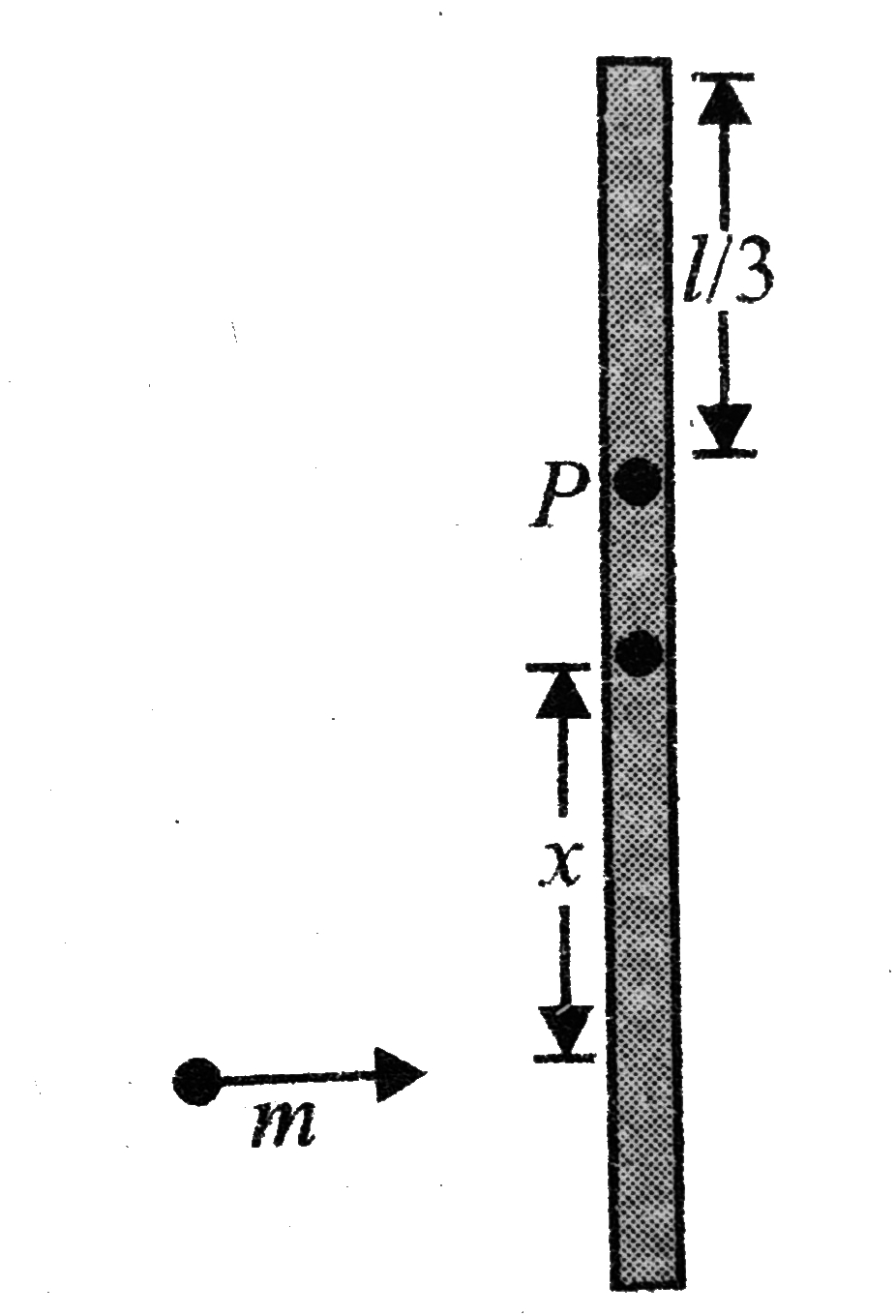
View SolutionA thin uniform rod of mass m and length l is kept on a smooth horizontal surface such that it can move freely. At what distance from centre of rod should a particle of mass m strike on the rod such that the point P at a distance l3 from the end of the rod is instantaneously at rest just after the elastic collision?
View SolutionA uniform flexible chain of mass m and length 2l hangs in equilibrium over a smooth horizontal pin of negligible diameter. One end of the chain is given a small vertical displacement so that the chain slips over the pin. The speed of chain when it leaves the pin is
View SolutionA uniform flexible chain of mass m and length l hangs in equilibrium over a smooth horizontal pin of neglible diameter. One end of the chain is given a small verticle displacement so that the chain slips over the pin. The speed of chain when it leaves pin is
View SolutionA uniform rod AB of mass m and length l at rest on a smooth horizontal surface . An impulse P is applied to the end B. The time taken by the rod to turn through a right angle is :

View Solution
