A proton, an electron, and a Helium nucleus, have the same energy.They are in circular orbits in a plane due to magnetic field perpendicular to the plane. Let rp,re and rHe be their respective radii, then,
re>rp=rHe
re<rp=rHe
re<rp<rHe
re>rp>rHe
The correct Answer is:A
To solve the problem, we need to find the relationship between the radii of the circular orbits of a proton, an electron, and a helium nucleus when they have the same energy and are subjected to a magnetic field perpendicular to their plane of motion.
1. Understanding the Motion in a Magnetic Field:
When a charged particle moves in a magnetic field perpendicular to its velocity, it experiences a centripetal force due to the magnetic field, causing it to move in a circular path. The radius r of the circular path is given by the formula:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
2. Relating Energy to Velocity:
The kinetic energy E of a particle is given by:
E=12mv2
From this, we can express mv in terms of energy:
mv=√2mE
3. Substituting in the Radius Formula:
Substituting mv into the radius formula gives:
r=√2mEqB
Since E and B are the same for all three particles, we can simplify our analysis to:
r∝√mq
4. Comparing the Radii:
Now we will compare the radii of the three particles:
- For the proton:
- Mass mp
- Charge qp
- For the electron:
- Mass me
- Charge qe
- For the helium nucleus (which is a He2+ ion):
- Mass mHe (approximately 4 times the mass of a proton)
- Charge qHe (2 times the charge of a proton)
Using the proportionality:
rp∝√mpqp,re∝√meqe,rHe∝√mHeqHe
5. Calculating the Ratios:
- For the proton:
rp∝√mpqp
- For the electron:
re∝√meqe=√mee
- For the helium nucleus:
rHe∝√mHeqHe=√4mp2e=√2mpe
6. Establishing the Relationships:
- Since me≪mp, it follows that re<rp.
- For the helium nucleus, since mHe=4mp and qHe=2e:
rHe=√2mpe>rp
7. Final Relationships:
Thus, we can conclude:
re<rp=rHe
Conclusion:
The final relationship between the radii is:
re<rp=rHe
When a charged particle moves in a magnetic field perpendicular to its velocity, it experiences a centripetal force due to the magnetic field, causing it to move in a circular path. The radius r of the circular path is given by the formula:
r=mvqB
where:
- m = mass of the particle
- v = velocity of the particle
- q = charge of the particle
- B = magnetic field strength
The kinetic energy E of a particle is given by:
E=12mv2
From this, we can express mv in terms of energy:
mv=√2mE
Substituting mv into the radius formula gives:
r=√2mEqB
Since E and B are the same for all three particles, we can simplify our analysis to:
r∝√mq
Now we will compare the radii of the three particles:
- For the proton:
- Mass mp
- Charge qp
- For the electron:
- Mass me
- Charge qe
- For the helium nucleus (which is a He2+ ion):
- Mass mHe (approximately 4 times the mass of a proton)
- Charge qHe (2 times the charge of a proton)
rp∝√mpqp,re∝√meqe,rHe∝√mHeqHe
- For the proton:
rp∝√mpqp
- For the electron:
re∝√meqe=√mee
- For the helium nucleus:
rHe∝√mHeqHe=√4mp2e=√2mpe
- Since me≪mp, it follows that re<rp.
- For the helium nucleus, since mHe=4mp and qHe=2e:
rHe=√2mpe>rp
Thus, we can conclude:
re<rp=rHe
The final relationship between the radii is:
re<rp=rHe
Topper's Solved these Questions
Similar Questions
A proton, a deuteron and an α- particle having the same kinetic energy are moving in circular trajectors in a constant magnetic field. If rp,rd and rα denote respectively the radii of the trajectories of these particles then
View SolutionAn electron, a proton, a deuteron and an alpha particle, each having the same speed are in a region of constant magnetic field perpendicular to the direction of the velocities of the particles. The radius of the circular orbits of these particles are respectively Re,Rp,Rd and Rα It follows that
View SolutionAn electron, a proton, a deuteron and an alpha particle, each having the same speed are in a region of constant magnetic field perpendicular to the direction of the velocities of the particles. The radius of the circular orbits of these particles are respectively Re,Rp,Rd and Rα It follows that
View SolutionThe magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
View SolutionA current (I) carrying circular wire of radius R is placed in a magnetic field B perpendicular to its plane. The tension T along the circumference of the wire is
View SolutionTwo particles A and B of masses mAandmB respectively and having the same charge are moving in a plane. A uniform magnetic field exists perpendicular to this plane. The speeds of the particles are vAandvB respectively and the trajectories are as shown in the figure. Then -
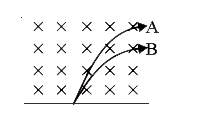
View SolutionIf an electron revolves around a nucleus in a circular orbit of radius R with frequency n, then the magnetic field produced at the center of the nucleus will be
View SolutionProton , deuton and alpha particle of same kinetic energy are moving in circular trajectories in a constant magnetic field. The radii of proton , deuteron and alpha particle are respectively rp,rdandrα. Which one of the following relation is correct?
View SolutionProton , deuton and alpha particle of same kinetic energy are moving in circular trajectories in a constant magnetic field. The radii of proton , deuteron and alpha particle are respectively rp,rdandrα. Which one of the following relation is correct?
View SolutionA proton, a deuteron and α-particle, whose kinetic energies are same, enter perpendicularly a uniform magnetic field. Compare the radii of their circular paths.
View Solution
