The magnetic field perpendicular to the plane of a conducting ring of radius r changes at the rate.dBdt . Then
the emf induced in the ring is πr2dBdt
the emf induced in the ring is 2πrdBdt
diametrically opposite points on the ring are at the same potential
all points on the ring are at the same potential
The correct Answer is:A, D
To solve the problem, we need to analyze the situation where the magnetic field perpendicular to the plane of a conducting ring is changing over time. We will use Faraday's law of electromagnetic induction to find the induced electromotive force (emf) in the ring.
1. Identify the Magnetic Flux (Φ):
The magnetic flux (Φ) through the conducting ring can be expressed as:
Φ=B⋅A
where B is the magnetic field and A is the area of the ring. For a ring of radius r, the area A is given by:
A=πr2
Thus, the magnetic flux becomes:
Φ=B⋅πr2
2. Differentiate the Magnetic Flux with Respect to Time:
To find the induced emf (E), we need to differentiate the magnetic flux with respect to time:
dΦdt=ddt(πr2B)
Since the radius r is constant, we can simplify this to:
dΦdt=πr2dBdt
3. Apply Faraday's Law of Electromagnetic Induction:
According to Faraday's law, the induced emf (E) in the ring is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Substituting our expression for dΦdt:
E=−πr2dBdt
4. Determine the Sign of the Induced emf:
The negative sign indicates the direction of the induced emf according to Lenz's law, but for the magnitude of the emf, we can write:
E=πr2dBdt
5. Analyze the Options:
Now we can analyze the options provided in the question:
- The first option states that the induced emf is E=πr2dBdt, which matches our derived expression.
- The second option states E=2πrdBdt, which is incorrect.
- The third option claims that diametrically opposite points on the ring are at the same potential, which is incorrect as there will be a potential difference due to the induced emf.
- The fourth option states that all points on the ring are at the same potential, which is correct because the induced emf distributes evenly around the ring.
Conclusion:
The correct answers are:
- The induced emf in the ring is given by E=πr2dBdt (Option 1).
- All points on the ring are at the same potential (Option 4).
The magnetic flux (Φ) through the conducting ring can be expressed as:
Φ=B⋅A
where B is the magnetic field and A is the area of the ring. For a ring of radius r, the area A is given by:
A=πr2
Thus, the magnetic flux becomes:
Φ=B⋅πr2
To find the induced emf (E), we need to differentiate the magnetic flux with respect to time:
dΦdt=ddt(πr2B)
Since the radius r is constant, we can simplify this to:
dΦdt=πr2dBdt
According to Faraday's law, the induced emf (E) in the ring is equal to the negative rate of change of magnetic flux:
E=−dΦdt
Substituting our expression for dΦdt:
E=−πr2dBdt
The negative sign indicates the direction of the induced emf according to Lenz's law, but for the magnitude of the emf, we can write:
E=πr2dBdt
Now we can analyze the options provided in the question:
- The first option states that the induced emf is E=πr2dBdt, which matches our derived expression.
- The second option states E=2πrdBdt, which is incorrect.
- The third option claims that diametrically opposite points on the ring are at the same potential, which is incorrect as there will be a potential difference due to the induced emf.
- The fourth option states that all points on the ring are at the same potential, which is correct because the induced emf distributes evenly around the ring.
The correct answers are:
- The induced emf in the ring is given by E=πr2dBdt (Option 1).
- All points on the ring are at the same potential (Option 4).
Similar Questions
the uniform magnetic field perpendicular to the plane of a conducting ring of radius a change at the rate of α, then
View Solutionthe uniform magnetic field perpendicualr to the plane of a conducting ring of radius a change at the rate of α, then
View SolutionThe figure shows a non conducting ring of radius R carrying a charge q. In a circular region of Radius r, a uniform magnetic field B perpendicular to the plane of the ring varies at a constant rate dBdt=β. The torque on the ring is

View SolutionA conducting loop of radius R is present in a uniform magnetic field B perpendicular to the plane of the ring. If radius R varies as a function of time t, as R=R0+t. The emf induced in the loop is

View SolutionA conducting ring of radius r and resistance R is placed in region of uniform time varying magnetic field B which is perpendicular to the plane of the ring. It the magnetic field is changing at a rate α, then the current induced in the ring is
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field. Find the instant of time at which EMF will be maximum & minimum respectively. (Figure:
 )
)
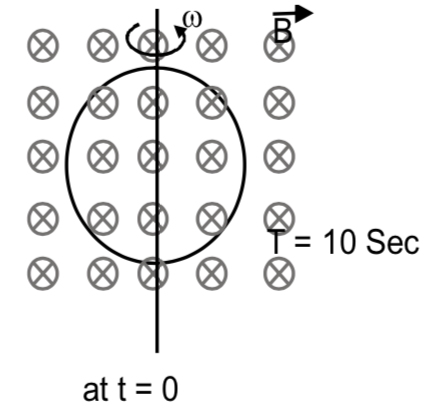
View SolutionA ring is rotated about diametric axis in a uniform magnetic field perpendicular to the plane of the ring. If initially the plane of the ring is perpendicular to the magnetic field.If T=10sec, find the instant of time at which EMF will be maximum & minimum respectively :
View SolutionA uniform but time varying magnetic field is present in a circular region of radius R. The magnetic field is perpendicular and into the plane of the loop and the magnitude of field is increasing at a constant rate α. There is a straight conducting rod of length 2R placed as shown in figure.
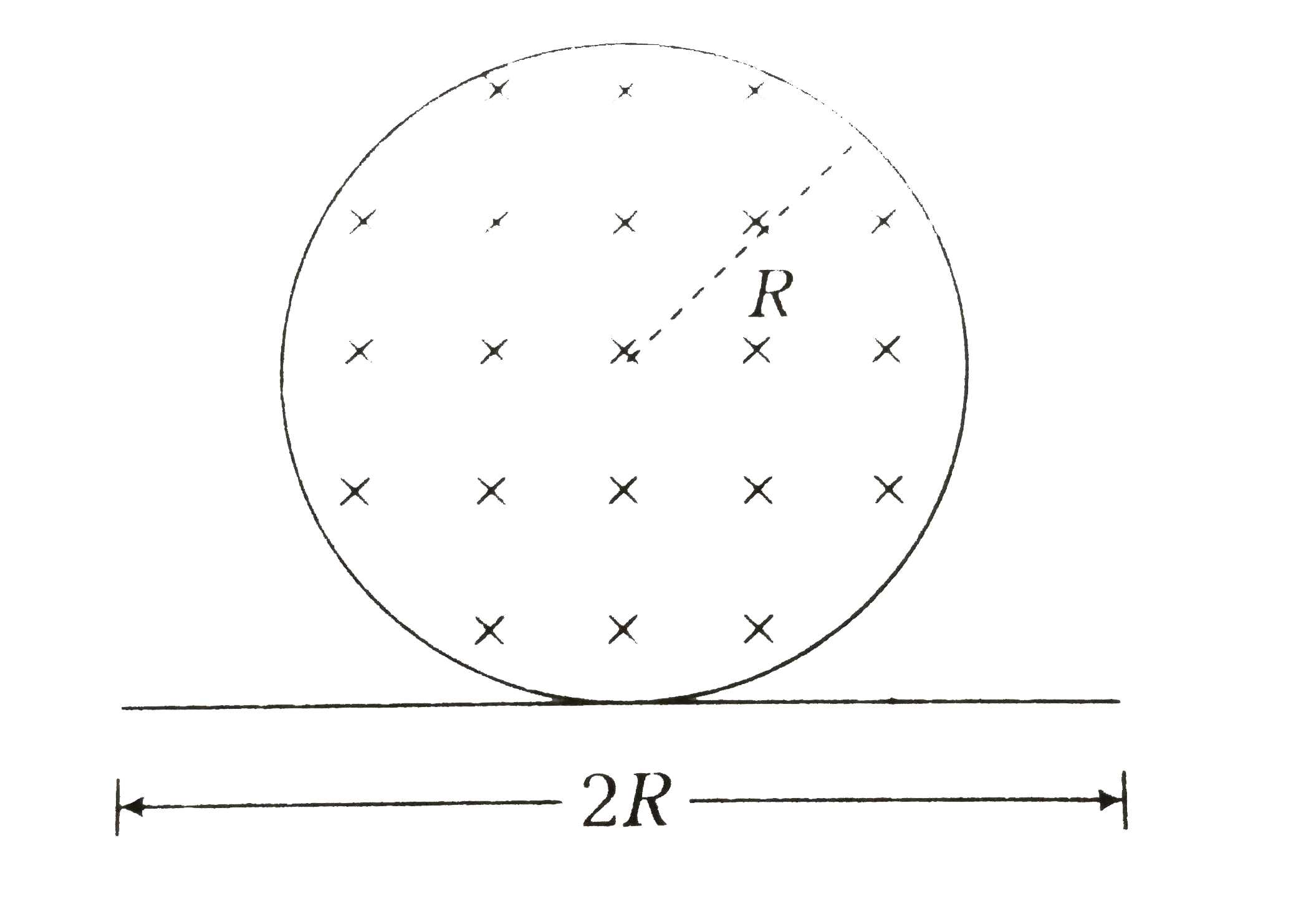
The magnitude of induced emf across the rod is
View SolutionA conducting light string is wound on the rim of a metal ring of radius r and mass m. The free end of the string is fixed to the ceiling. A vertical infinite smooth conducting plane is always tangent to the ring as shown in the figure. A uniform magnetic field Bis applied perpendicular to the plane of the ring. The ring is always inside the magnetic field. The plane and the strip are connected by a resistance R. When the ring is released, find

a. the curent in the resistance R as as function of time.
b. the terminal velocity of the ring.
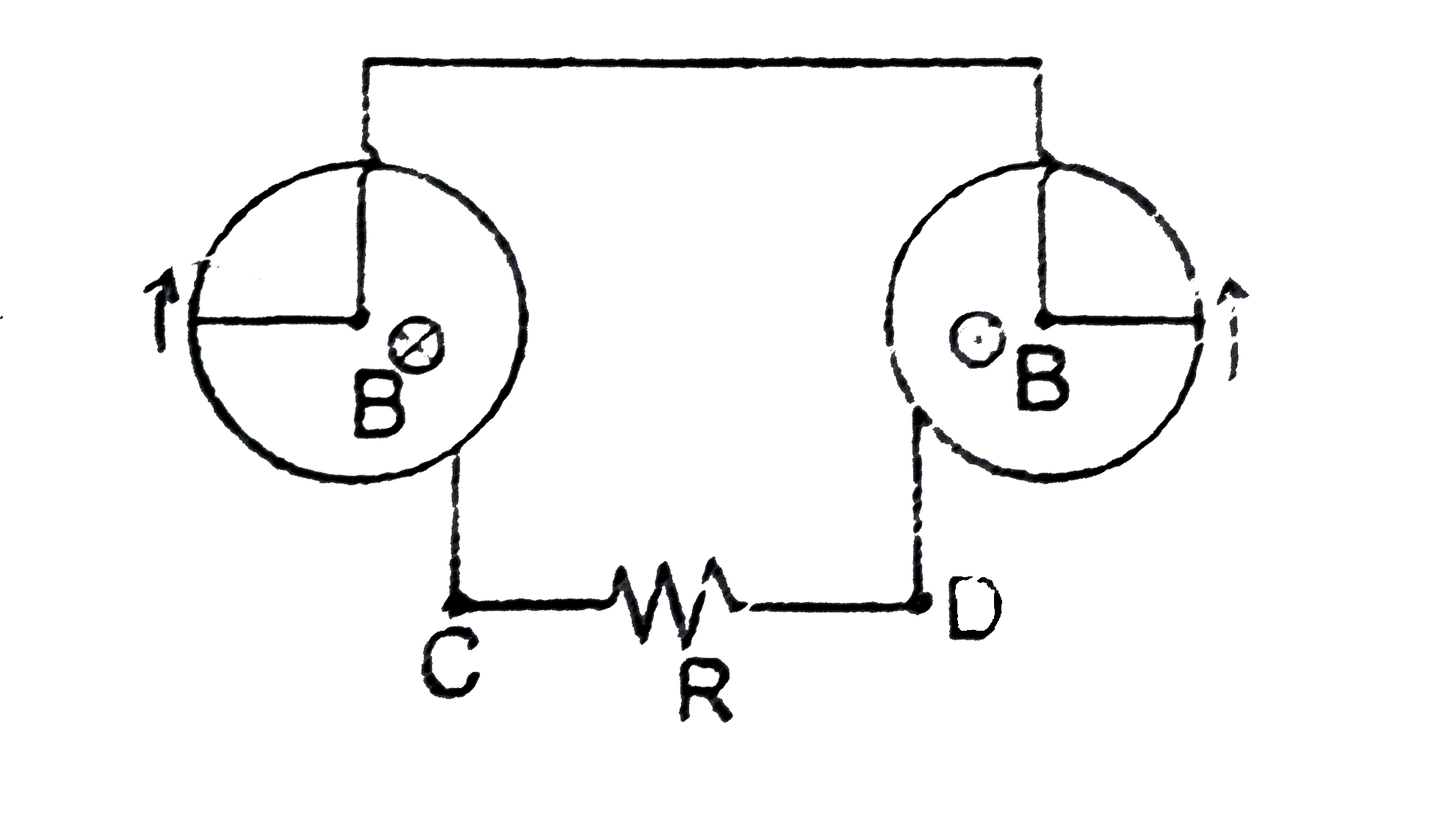
View SolutionIn the figure there are two identical conducting rods each of length a rotating with angular speed ω is the direction shown.One end of each rod touches a conducting ring.Magnetic field B exists perpendicular to the plane of the rings.The rods the conducting rings and the lead wires and resistanceless.Find the magnitude and direction of current in the resistance R.
View Solution