A magnetic compass needl oscillates 30 times per minute at a place where the dip is 45∘ and 40 times per minute where the dip is 30∘ if B1 and B2 are respectively the total magnetic field due to the earth at the two places then the ratio B1/B2 is best given by
1.8
0.7
3.6
2.2
The correct Answer is:C
To solve the problem, we need to find the ratio of the total magnetic fields B1 and B2 at two different locations where the compass needle oscillates at different frequencies and dip angles.
Step 1: Understand the relationship between frequency and magnetic field
The frequency of oscillation F of a magnetic compass needle is given by the formula:
F=12π√mBI
where:
- m is the magnetic moment,
- B is the magnetic field,
- I is the moment of inertia.
Step 2: Set up the equations for the two locations
For the first location (where the dip angle is 45∘ and frequency is 30 oscillations per minute):
F1=30 oscillations/min=3060 oscillations/sec=0.5 Hz
Using the formula:
0.5=12π√mB1cos(45∘)I
Squaring both sides gives:
(0.5⋅2π)2=mB1cos(45∘)I
For the second location (where the dip angle is 30∘ and frequency is 40 oscillations per minute):
F2=40 oscillations/min=4060 oscillations/sec=23 Hz
Using the formula:
23=12π√mB2cos(30∘)I
Squaring both sides gives:
(23⋅2π)2=mB2cos(30∘)I
Step 3: Simplify the equations
From the first location:
(0.5⋅2π)2Imcos(45∘)=B1
From the second location:
(23⋅2π)2Imcos(30∘)=B2
Step 4: Find the ratio B1B2
Now, we can find the ratio B1B2:
B1B2=(0.5⋅2π)2cos(30∘)(23⋅2π)2cos(45∘)
Canceling out common terms:
B1B2=(0.5)2cos(30∘)(23)2cos(45∘)
Substituting the values of cos(30∘)=√32 and cos(45∘)=1√2:
B1B2=(0.5)2⋅√32(23)2⋅1√2
Step 5: Calculate the ratio
Calculating the values:
=0.25⋅√3249⋅1√2
=0.25⋅√3⋅9√24
=0.25⋅9√64
=9√616
Final Step: Approximate the value
Calculating this gives us the ratio B1B2≈0.7.
Conclusion
Thus, the ratio B1B2 is approximately 0.7.
---
The frequency of oscillation F of a magnetic compass needle is given by the formula:
F=12π√mBI
where:
- m is the magnetic moment,
- B is the magnetic field,
- I is the moment of inertia.
For the first location (where the dip angle is 45∘ and frequency is 30 oscillations per minute):
F1=30 oscillations/min=3060 oscillations/sec=0.5 Hz
Using the formula:
0.5=12π√mB1cos(45∘)I
Squaring both sides gives:
(0.5⋅2π)2=mB1cos(45∘)I
F2=40 oscillations/min=4060 oscillations/sec=23 Hz
Using the formula:
23=12π√mB2cos(30∘)I
Squaring both sides gives:
(23⋅2π)2=mB2cos(30∘)I
From the first location:
(0.5⋅2π)2Imcos(45∘)=B1
From the second location:
(23⋅2π)2Imcos(30∘)=B2
Now, we can find the ratio B1B2:
B1B2=(0.5⋅2π)2cos(30∘)(23⋅2π)2cos(45∘)
Canceling out common terms:
B1B2=(0.5)2cos(30∘)(23)2cos(45∘)
Substituting the values of cos(30∘)=√32 and cos(45∘)=1√2:
B1B2=(0.5)2⋅√32(23)2⋅1√2
Calculating the values:
=0.25⋅√3249⋅1√2
=0.25⋅√3⋅9√24
=0.25⋅9√64
=9√616
Calculating this gives us the ratio B1B2≈0.7.
Thus, the ratio B1B2 is approximately 0.7.
Topper's Solved these Questions
Similar Questions
A compass needle oscillates 20 times per minute at a place where the dip is 45∘ and 30 times per minute where the dip is 30∘. Compare the total magnetic field due to the earth at the two places.
View SolutionA magnet oscillating in a horizontal plane has a time period of 2 seconds at a place where the angle of dip is 30∘ and 3 seconds at another place where the angle of dip is 60∘. The retio of resultant magnetic field at the two places is
View SolutionA cell is connected between the point A and C of a circular conductor ABCD of centre O,∠AOC=60∘. If B1 and B2 are the magnitude of magnetic fields at O due to the currents in ABC and ADC respectively, the ratio of B1/B2 is.
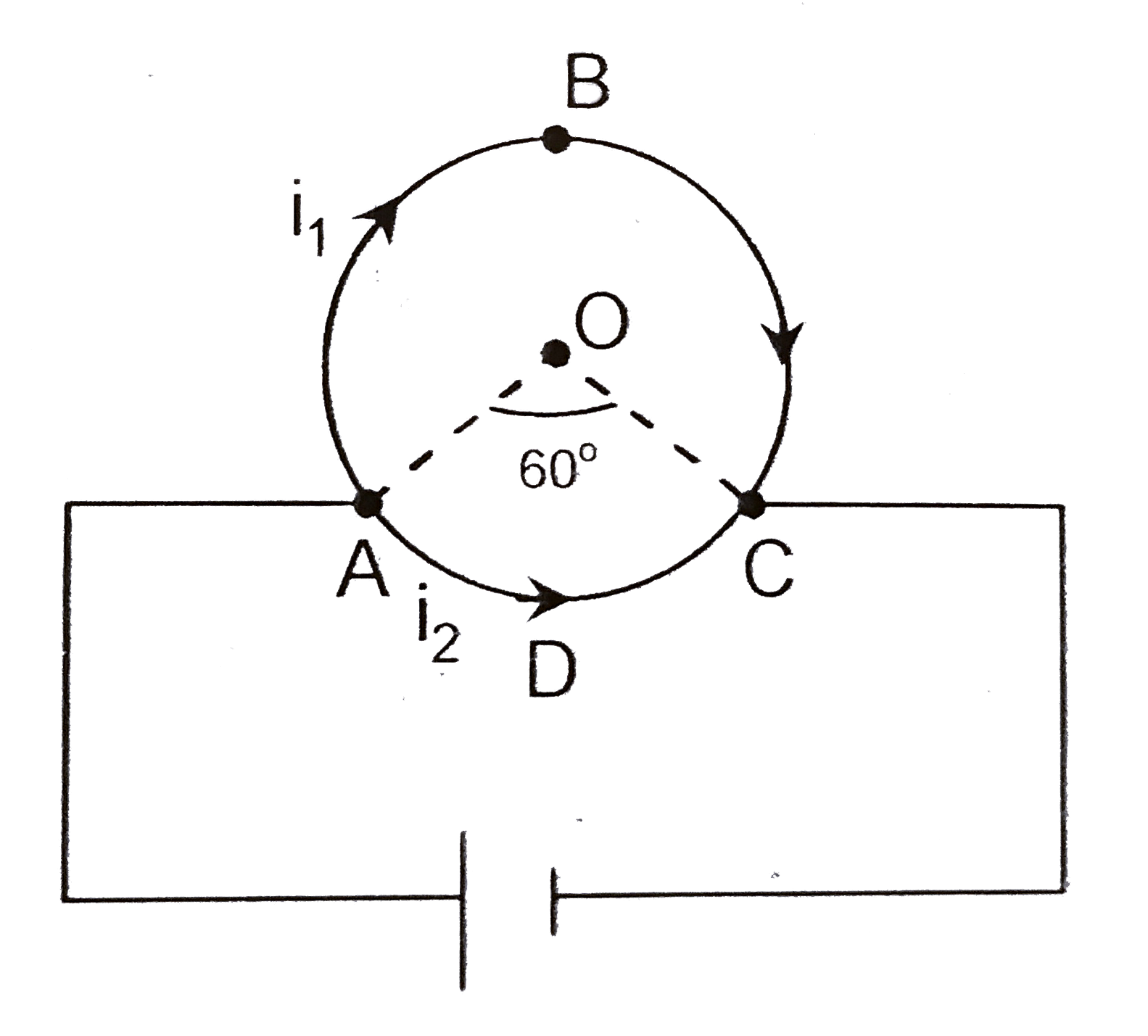
View SolutionA magnet is suspended in such a way that it oscillates in the horizontal plane. It makes 20 oscillations per minute at a place where dip angle is 30∘ and 15 oscillations minute at a place where dip angle is 60∘. The ratio of total earth's magnetic field at the two places is
View SolutionAt a certain place, the angle of dip is 30∘ and the horizontal component of earth's magnetic field is 50μT. The total magnetic field (in μT) of the earth at this place, is
View SolutionA cell is connected between the points A and C of a circular conductor ABCD of centre 'O'.∠AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is
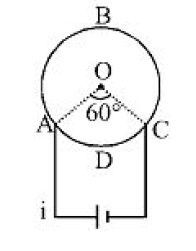
View SolutionA cell is connected between the points A and C of a circular conductor ABCD of centre O .∠ AOC=60∘. IfB1andB2 are the magnitudes of the magnetic fields at O due to the currents in ABC and ADC respectively, the ratio B1B2, is

View SolutionAt a certain place the angle of dip is 30∘ and the horizontal component of earth's magnetic field is 0.50 oersted. The earth's total magnetic field is
View SolutionTwo coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
View SolutionIf the angle of dip at two places are 30∘ and 45∘ respectively, then the ratio of horizontal components of earth's magnetic field at the two places will be
View Solution
