Two coils are having magnetic field B and 2B at their centres and current i and 2i then the ratio of their radius is
1:2
2:1
1:1
4:1
The correct Answer is:C
To solve the problem, we will use the formula for the magnetic field at the center of a circular coil. The magnetic field B at the center of a coil is given by the formula:
B=μ0I2R
where:
- B is the magnetic field,
- μ0 is the permeability of free space,
- I is the current flowing through the coil,
- R is the radius of the coil.
Step 1: Write the magnetic field equations for both coils
For the first coil:
B=μ0I2R1
For the second coil:
2B=μ0(2I)2R2
Step 2: Simplify the equations
From the first coil:
B=μ0I2R1(1)
From the second coil:
2B=μ0(2I)2R2⟹2B=μ0IR2(2)
Step 3: Set up the ratio of the two equations
Now, we will divide equation (1) by equation (2):
B2B=μ0I2R1μ0IR2
Step 4: Cancel out common terms
Canceling out B and μ0I from both sides, we have:
12=R22R1
Step 5: Rearrange the equation to find the ratio of radii
Cross-multiplying gives:
R2=R1
Thus, the ratio of the radii R1 to R2 is:
R1R2=1
Final Answer
The ratio of the radii R1:R2 is 1:1.
---
- B is the magnetic field,
- μ0 is the permeability of free space,
- I is the current flowing through the coil,
- R is the radius of the coil.
B=μ0I2R1
2B=μ0(2I)2R2
B=μ0I2R1(1)
2B=μ0(2I)2R2⟹2B=μ0IR2(2)
B2B=μ0I2R1μ0IR2
12=R22R1
R2=R1
R1R2=1
The ratio of the radii R1:R2 is 1:1.
Topper's Solved these Questions
Similar Questions
The magnetic field at the centre of the current carrying coil is
View SolutionRatio of magnetic field at the centre of a current carrying coil of radius R and at a distance of 3R on its axis is
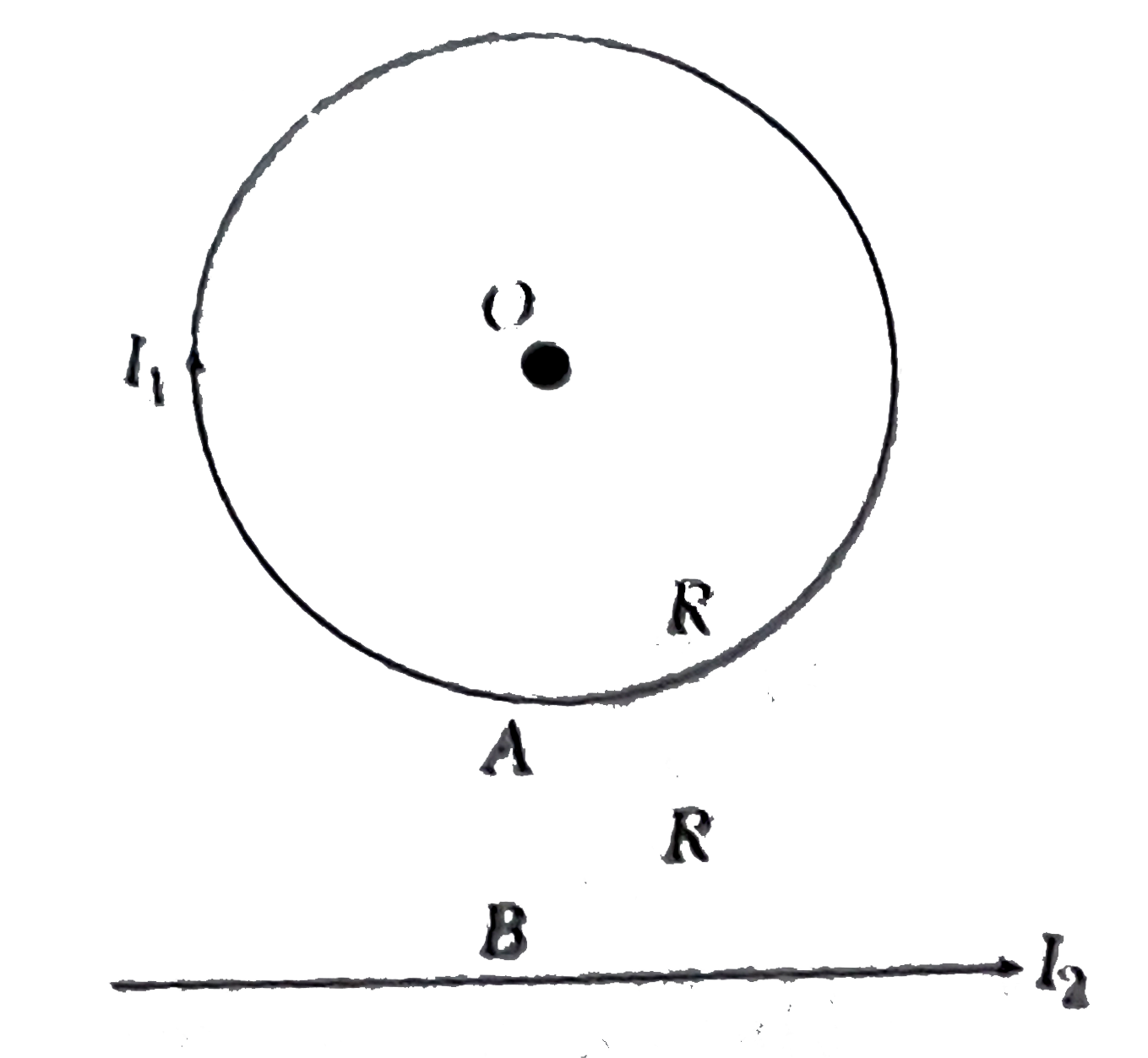
View SolutionIn the diagram I1,I2 are the strength of the currents in the loop and straight conductors respectively OA=AB=R. the net magnetic field at the centre O is zero . Then the ratio of the currents in the loop and the straight conductor is
View SolutionCurrent I A flowing in a circular coil of radius r. then the magnetic induction at the centre is B. If the current is doubled then the magnetic induction will be
View SolutionThe ratio of the magnetic field at the centre of a current carrying coil of the radius a and at distance 'a' from centre of the coil and perpendicular to the axis of coil is
View SolutionA long staright wire of radius a carries a steady current I. The curent is unifromly distributed over its cross-section. The ratio of the magnetic fields B and B' , at radial distances a2 and 2a respectively from the axis of the wire is:
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionTwo similar coils are kept mutually perpendicular such that their centres coincide. At the centre, find the ratio of the magnetic field due to one coil and the resultant magnetic field by both coils, if the same current is flown
View SolutionA current I is flowing in a straight conductor of length L. The magnetic induction at a point distant L4 from its centre will be
View SolutionThe ratio of the magnetic field at the centre of a current carrying circular coil to its magnetic moment is x. If the current and radius both are doubled the new ratio will become
View Solution
