At a brass wire of 1mm radius is hung from the ceiling. A small mass, M is hung from the free end of the wire. When the wire is cooled down from to it regains its original length of 0.2 m the value of M is close to (coefficient of linear expansion and young's modulus of brass are and respectively
9kg
0.5kg
1.5 kg
0.9 kg
The correct Answer is:C
To solve the problem step by step, we need to analyze the situation involving the brass wire and the mass hanging from it.
Step 1: Understand the problem
We have a brass wire that is initially at a temperature of 40∘C and has a radius of 1mm. A mass M is hung from the wire. When the temperature drops to 20∘C, the wire regains its original length of 0.2m. We need to find the value of M.
Step 2: Identify the relevant formulas
1. Change in length due to temperature change:
ΔL=αLΔT
where:
- ΔL = change in length
- α = coefficient of linear expansion
- L = original length
- ΔT = change in temperature
2. Stress and strain relationship:
Stress=FA=mgA
where:
- F = force due to the mass M
- A = cross-sectional area of the wire
3. Young's Modulus:
Y=StressStrain=F/AΔL/L
Step 3: Calculate the change in length due to cooling
Given:
- ΔT=40∘C−20∘C=20∘C
- α=10−5°C−1
- L=0.2m
Substituting into the formula for change in length:
ΔL=αLΔT=(10−5)(0.2)(20)=4×10−5m
Step 4: Calculate the cross-sectional area of the wire
The radius r of the wire is 1mm=1×10−3m.
The area A is given by:
A=πr2=π(1×10−3)2=π×10−6m2
Step 5: Relate stress and strain
From Young's modulus:
Y=mg/AΔL/L
Rearranging gives:
mg=Y⋅A⋅ΔLL
Step 6: Substitute known values
Substituting Y=1011N/m2, A=π×10−6m2, ΔL=4×10−5m, and L=0.2m:
mg=(1011)⋅(π×10−6)⋅4×10−50.2
Step 7: Calculate mg
Calculating the right-hand side:
mg=(1011)⋅(π×10−6)⋅(2×10−4)=2π×101N
Thus,
M=2π×101g=2π×10110=2πkg
Step 8: Final calculation
Using π≈3.14:
M≈2×3.14=6.28kg
Final Answer:
The value of M is approximately 6.28kg.
We have a brass wire that is initially at a temperature of 40∘C and has a radius of 1mm. A mass M is hung from the wire. When the temperature drops to 20∘C, the wire regains its original length of 0.2m. We need to find the value of M.
1. Change in length due to temperature change:
ΔL=αLΔT
where:
- ΔL = change in length
- α = coefficient of linear expansion
- L = original length
- ΔT = change in temperature
Stress=FA=mgA
where:
- F = force due to the mass M
- A = cross-sectional area of the wire
Y=StressStrain=F/AΔL/L
Given:
- ΔT=40∘C−20∘C=20∘C
- α=10−5°C−1
- L=0.2m
ΔL=αLΔT=(10−5)(0.2)(20)=4×10−5m
The radius r of the wire is 1mm=1×10−3m.
The area A is given by:
A=πr2=π(1×10−3)2=π×10−6m2
From Young's modulus:
Y=mg/AΔL/L
Rearranging gives:
mg=Y⋅A⋅ΔLL
Substituting Y=1011N/m2, A=π×10−6m2, ΔL=4×10−5m, and L=0.2m:
mg=(1011)⋅(π×10−6)⋅4×10−50.2
Calculating the right-hand side:
mg=(1011)⋅(π×10−6)⋅(2×10−4)=2π×101N
Thus,
M=2π×101g=2π×10110=2πkg
Using π≈3.14:
M≈2×3.14=6.28kg
The value of M is approximately 6.28kg.
Topper's Solved these Questions
Similar Questions
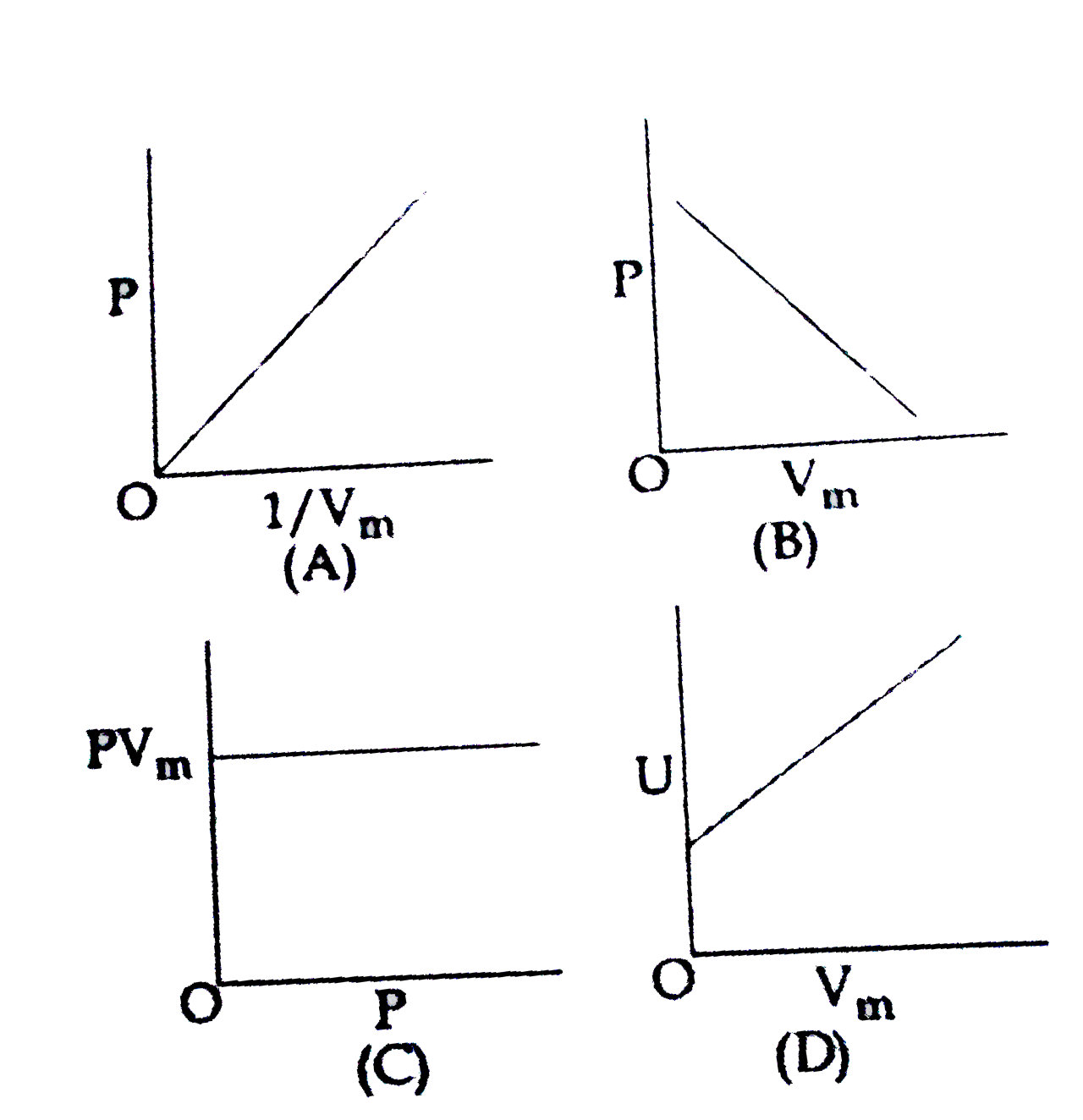
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionAt 40^(@)C a brass wire of 1mm radius is hung from the ceiling. A small mass, M is hung from the free end of the wire. When the wire is cooled down from 40^(@)C to 20^(@)C it regains its original length of 0.2 m the value of M is close to (coefficient of linear expansion and young's modulus of brass are 10^(-5)//.^(@)C and 10^(11)//N//m^(2) respectively g=10ms^(-2))
View SolutionSteel wire of length 'L' at 40^@C is suspended from the ceiling and then a mass 'm' is hung from its free end. The wire is cooled down from 40^@C to 30^@C to regain its original length 'L'. The coefficient of linear thermal expansion of the steel is 10^-5//^@C , Young's modulus of steel is 10^11 N//m^2 and radius of the wire is 1mm. Assume that L gt gt diametere of the wire. Then the value of 'm' in kg is nearly
View SolutionYoung's modulus of brass and steel are 10×1010N/m and 2×1011N/m2, respectively. A brass wire and a steel wire of the same length are extended by 1mm under the same force. The radii of the brass and steel wires are RB and RS. respectively. Then
View SolutionA brass wire 1.8 m long at 27^(@)C is held taut with negligible tension between two rigid supports. Diameter of the wire is 2 mm, its coefficient of linear expasion, alpha_("Brass") = 2 xx 10^(-5) .^(@)C^(-1) and its young's modulus, Y_("Brass") = 9xx 10^(10) N m^(-2) . If the wire is cooled to a temperature -39^(@)C , tension developed in the wire is
View SolutionThe Young's modulus of brass and steel are respectively 1.0×1011N/m2 and 2.0×1011N/m2 . A brass wire and steel wire of the same length are extended by 1mm each under the same force. If radii of brass and steel wires are RB and RS respectively,. then
View SolutionA brass wire of length 5 m and cross section area 10^(-6) m^(2) hung from rigid support with brass weight of volume 10^(-3)m^(3) hanging from other end. Then the decrease in length of the wire when brass weight is completely immersed in water is, (g=10m//s^(2), Y_("brass")=10^(11)N//m^(2), rho_(w)=10^(3)kg//m^(3))
View SolutionIf a uniform brass wire of length 5 m and radius 10−3 m is extended by 10−3m, then the energy stored in the wire will be
(Young's modulus for brass =10×1010N/m2)
View SolutionL लम्बाई का स्टील का तार, जो 40∘C तापमान पर है, को छत से लटका कर उसके मुक्त सिरे पर द्रव्यमान m संलग्न किया जाता है | जब तार को ठण्डा करके उसका तापमान 40∘C से 30∘C लाने पर उसकी लम्बाई फिर से L हो जाती है | स्टील का तापीय प्रसार गुणांक 10−5/.∘C है, यंग प्रत्यास्थता गुणांक 1011 न्यूटन मी−2 है तथा तार की त्रिज्या 1 मिमी है | मानें कि L>> तार का व्यास m का किग्रा में मान लगभग है |
View Solution40∘C तापमान पर 1mm त्रिज्या का पीतल का एक तार छत से लटकाया गया है। तार के मुक्त सिरे से M द्रव्यमान के एक छोटे पिण्ड को लटकाया गया है। जब तार 40∘C को 20∘C से पर ठण्डा करते है, तो वह वापस अपनी पुरानी लम्बाई 0.2 m को प्राप्त कर लेता है। M का निकटतम मान होगा (पीतल का रेखीय प्रसार गुणांक तथा यंग प्रत्यास्थ गुणांक क्रमशः है
105/∘C तथा 1011N/m एवं g=10ms−2)
View SolutionA copper wire of length l and radius 2 mm is suspended from a fixed support vertically and a mass m is hung from its other end. The wire initially at 30^@C is cooled down to 20^@C to bring it back to its original length l . The coefficient of linear thermal expansion of the copper is 1.7 xx 10^(-5) "'^@C^(-1) . If l >> the diameter of wire,then find the value of m/5 in kg close to nearest integer. Take, g = 10 m//s^2 , Y = 1.1 xx 10^11 N//m^2
View SolutionSteel wire of length 'L' at 40∘C is suspended from the ceiling and then a mass 'm' is hung from its free end. The wire is cooled dowa from 40∘C to 30∘C to regain its original length 'L'. The coefficient of linear thermal expansiou of the steel is 10−5/∘C, Young's modulus of steel is 1011N/m2 and radius of the wire is 1 mm. Assume that L>> diameter of the wire. Then the value of 'm' in kg is nearly
View SolutionA light rod of length 2 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10^(-3) m^2 and the other is of brass of cross-section 2 xx 10^(-3) m^2 . Find out the position along the rod at which a weight may be hung to produce, i) equal stress in both wires ii) equal strains in both wires Young's modulus of brass = 1 xx 10^11 N//m^2 Young's modulus of steel = 2 xx 10^11 N//m^2
View Solution
