There are two long co-axial solenoids of same length l. The inner and other coils have redii r1 and r2 and number of turns per unti length n1 and n2 respectively .The reatio of mutual inductance to the self - inductance of the inner- coil is : (A) n1n2 (B) n2n1.r1r2 (C) n2n1.r22r21 (D) n2n1
n1n2
n2n1.r1r2
n2n1.r22r21
n2n1
To solve the problem, we need to find the ratio of the mutual inductance (M) to the self-inductance (L) of the inner solenoid. Let's break it down step by step.
Step 1: Write the formula for mutual inductance (M)
The mutual inductance M between two coaxial solenoids can be expressed as:
M=μ0⋅n1⋅n2⋅πr22⋅l
where:
- μ0 is the permeability of free space,
- n1 is the number of turns per unit length of the inner solenoid,
- n2 is the number of turns per unit length of the outer solenoid,
- r2 is the radius of the outer solenoid,
- l is the length of the solenoids.
Step 2: Write the formula for self-inductance (L) of the inner solenoid
The self-inductance L of the inner solenoid can be expressed as:
L=μ0⋅n21⋅πr21⋅l
where:
- r1 is the radius of the inner solenoid.
Step 3: Find the ratio ML
Now, we need to find the ratio of mutual inductance to self-inductance:
ML=μ0⋅n1⋅n2⋅πr22⋅lμ0⋅n21⋅πr21⋅l
Step 4: Simplify the expression
We can cancel out the common terms:
- μ0 cancels out,
- π cancels out,
- l cancels out.
Thus, we have:
ML=n1⋅n2⋅r22n21⋅r21
Step 5: Further simplification
Now, we can simplify the expression:
ML=n2⋅r22n1⋅r21
Step 6: Identify the correct option
From the options given, we can see that the ratio ML is not directly listed. However, we can express it in terms of n2/n1 and the ratio of the squares of the radii:
ML=n2n1⋅r22r21
Thus, the correct answer is:
ML=n2n1⋅r22r21
Final Answer
The correct option is (C) n2n1⋅r22r21.
---
The mutual inductance M between two coaxial solenoids can be expressed as:
M=μ0⋅n1⋅n2⋅πr22⋅l
where:
- μ0 is the permeability of free space,
- n1 is the number of turns per unit length of the inner solenoid,
- n2 is the number of turns per unit length of the outer solenoid,
- r2 is the radius of the outer solenoid,
- l is the length of the solenoids.
The self-inductance L of the inner solenoid can be expressed as:
L=μ0⋅n21⋅πr21⋅l
where:
- r1 is the radius of the inner solenoid.
Now, we need to find the ratio of mutual inductance to self-inductance:
ML=μ0⋅n1⋅n2⋅πr22⋅lμ0⋅n21⋅πr21⋅l
We can cancel out the common terms:
- μ0 cancels out,
- π cancels out,
- l cancels out.
ML=n1⋅n2⋅r22n21⋅r21
Now, we can simplify the expression:
ML=n2⋅r22n1⋅r21
From the options given, we can see that the ratio ML is not directly listed. However, we can express it in terms of n2/n1 and the ratio of the squares of the radii:
ML=n2n1⋅r22r21
ML=n2n1⋅r22r21
The correct option is (C) n2n1⋅r22r21.
Topper's Solved these Questions
Similar Questions
Find the mutual inductance of two long concentric solenoids for a length l. The area of cross-section of inner solenoid is A and number of turns per unit length are n1 and n2.

View SolutionTwo coaxil solenoids 1 and 2 of the same length are set so that one is inside the other. The number of turns per unit length are n1 and n2. The current i1 and i2 are flowing in opposite directions. The magnetic field inside the inner coil is zero. This is possible when
View SolutionTwo coaxial long solenoids of equal length have current, i1,i2, number of turns per unit length n1,n2 and radius r1,r2 respectively. If n1i1=n2i2 and the two solenoids carry current in opposite sense, the magnetic energy stored per unit length is [r2>r1]
View SolutionA solenoid S1 is placed inside another solenoid S2 as shown in the fig. The radii of the inner and the outer solenoids are r1 and r2 respectively and the numbers of turns per unit length are n1 and n2 respectively. Consider a length I of each solenoid. Calculate the mutual inductance between them.

View SolutionDefine mutual inductance between two long coaxial solenoids. Find out the expression for the mutual of inner solenoid of length 1 having the radius r1 and the number of turns n1 per unit length due to the second other solenoid of same length and n2 number of turns per unit length.
View SolutionA long solenoid of length L, cross section A having N1 turns has about its center a small coil of N2 turns as shows in Fig The mutual inductance of two circuits is
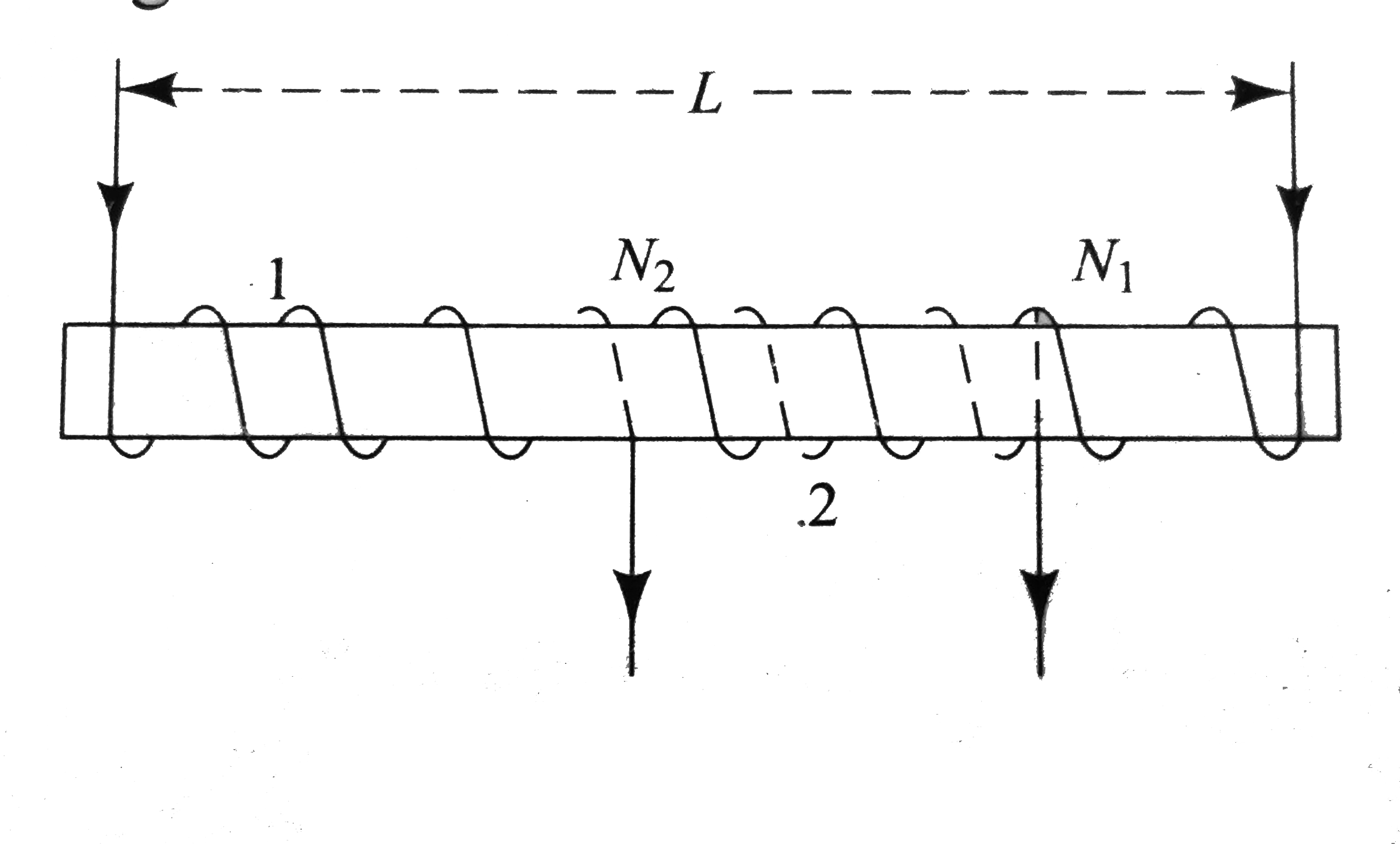
View SolutionFor the Paschen series thr values of n1 and n2 in the expression ΔE=RHc[1n21−1n22] are
View SolutionnCr+1+nCr−1+2.nCr=
View Solution.nCr+2.nCr−1+.nCr−2=
View SolutionLet Sn denote the sum of first n terms of a G.P. whose first term and common ratio are a and r respectively. On the basis of above information answer the following question: S1+S2+S3+..+Sn= (A) na1−r−ar(1−rn)(1−r)2 (B) na1−r−ar(1+rn)(1+r)2 (C) na1−r−a(1−rn)(1−r)2 (D) none of these
View Solution
