The region between y =0 and y=d constains a magnetic field →B=B→z. A particle of mass m and charge q enters of the region with a velocity →v=v→i. If d=mv2qB the acceleration of the charged particle at the point of its emergence at the other side is :
qvBm(12ˆi−√32ˆj)
qvBm(√32ˆi−12ˆj)
qvBm(−ˆj+ˆi√2)
qvBm(ˆi+ˆj√2)
To solve the problem, we need to analyze the motion of a charged particle in a magnetic field. Let's break down the solution step by step.
Step 1: Understand the setup
The particle of mass m and charge q enters a region where there is a magnetic field →B=B^k (along the z-axis). The particle enters with a velocity →v=v^i (along the x-axis). The region of the magnetic field extends from y=0 to y=d, where d=mv2qB.
Step 2: Determine the magnetic force
The magnetic force →F acting on the charged particle is given by the Lorentz force equation:
→F=q→v×→B
Substituting the values:
→F=q(v^i)×(B^k)=qvB(^i×^k)=qvB(−^j)
Thus, the magnetic force acts in the negative y-direction.
Step 3: Calculate the radius of the circular motion
The magnetic force also acts as the centripetal force required for circular motion. The centripetal force Fc is given by:
Fc=mv2r
Setting the magnetic force equal to the centripetal force:
qvB=mv2r
From this, we can solve for the radius r:
r=mvqB
Step 4: Relate the distance d to the radius
We know from the problem statement that d=mv2qB. This indicates that the particle will travel a quarter of the circular path when it exits the magnetic field.
Step 5: Determine the acceleration
The only acceleration acting on the particle is the centripetal acceleration ac, which is directed towards the center of the circular path:
ac=v2r
Substituting the expression for r:
ac=v2mvqB=qBvm
Step 6: Direction of the acceleration
At the point of emergence, the particle is moving in the x-direction, and the centripetal acceleration is directed towards the center of the circular path (which is in the negative y-direction). Therefore, the acceleration vector can be expressed as:
→a=−qBvm^j
Final Answer
The acceleration of the charged particle at the point of its emergence at the other side is:
→a=−qBvm^j
The particle of mass m and charge q enters a region where there is a magnetic field →B=B^k (along the z-axis). The particle enters with a velocity →v=v^i (along the x-axis). The region of the magnetic field extends from y=0 to y=d, where d=mv2qB.
The magnetic force →F acting on the charged particle is given by the Lorentz force equation:
→F=q→v×→B
Substituting the values:
→F=q(v^i)×(B^k)=qvB(^i×^k)=qvB(−^j)
Thus, the magnetic force acts in the negative y-direction.
The magnetic force also acts as the centripetal force required for circular motion. The centripetal force Fc is given by:
Fc=mv2r
Setting the magnetic force equal to the centripetal force:
qvB=mv2r
From this, we can solve for the radius r:
r=mvqB
We know from the problem statement that d=mv2qB. This indicates that the particle will travel a quarter of the circular path when it exits the magnetic field.
The only acceleration acting on the particle is the centripetal acceleration ac, which is directed towards the center of the circular path:
ac=v2r
Substituting the expression for r:
ac=v2mvqB=qBvm
At the point of emergence, the particle is moving in the x-direction, and the centripetal acceleration is directed towards the center of the circular path (which is in the negative y-direction). Therefore, the acceleration vector can be expressed as:
→a=−qBvm^j
The acceleration of the charged particle at the point of its emergence at the other side is:
→a=−qBvm^j
Topper's Solved these Questions
Similar Questions
A particle of mass m and charge Q moving with a velocity v enters a region on uniform field of induction B Then its path in the region is s
View SolutionA charge particle of mass m and charge q is projected with velocity v along y-axis at t=0.

Find the velocity vector and position vector of the particle →v(t)and→r(t) in relation with time.View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation of the particle as it comes out of the magnetic field if ihe width d of the region is
2mvqB
 View Solution
View SolutionA non-uniform magnetic field →B=B0(1+yd)(−ˆk) is present in region of space in between y=0&y=d.The lines are shown in the diagram.A particle of mass m and positive charge q is moving.Given an initial velocity →v=v0ˆi.Find the components of velocity of the particle when it leaves the field.
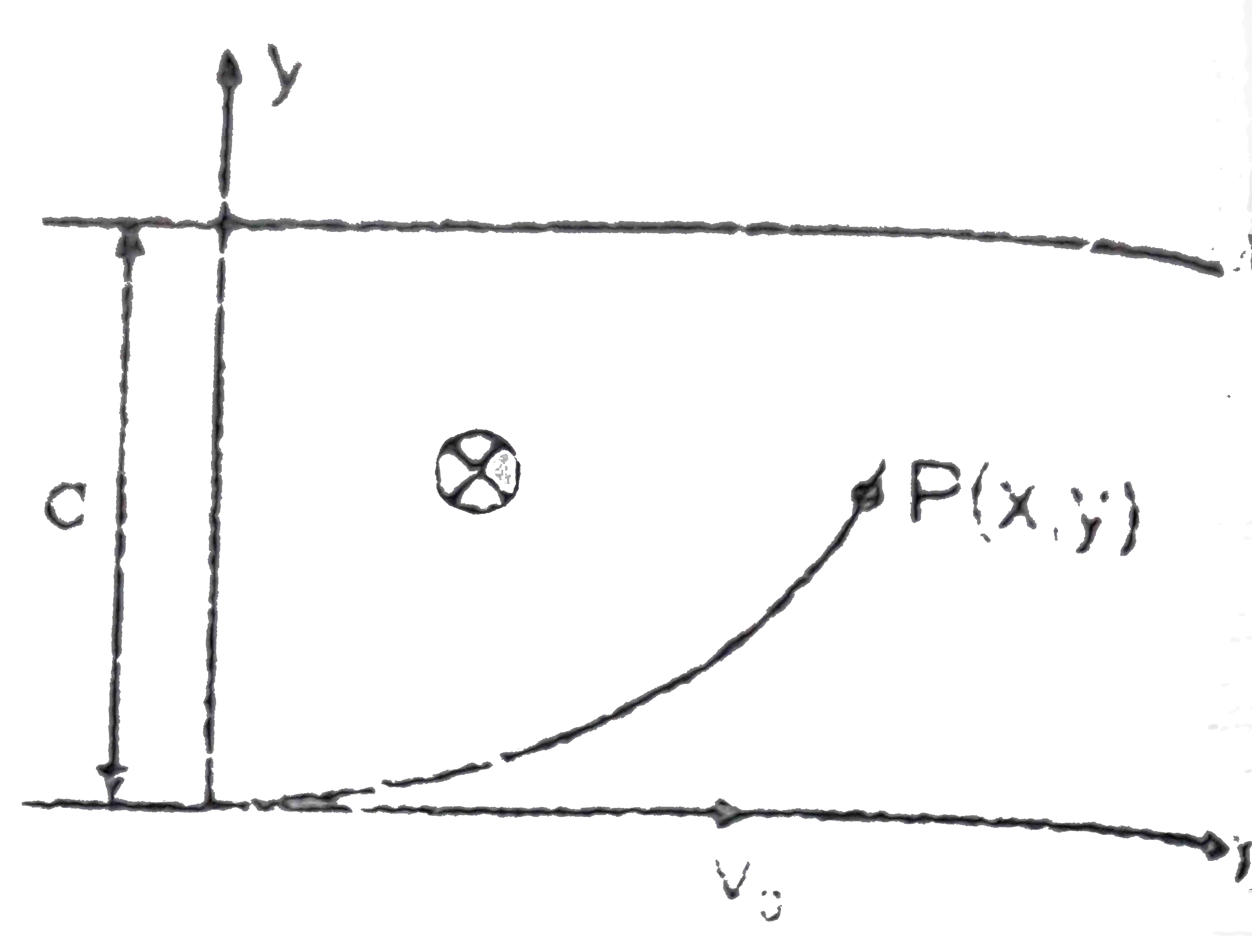 View Solution
View SolutionThe figure shows two regions of uniform magnetic field of strengths 2B and 2B. A charged particle of mass m and charge q enters the region of the magnetic field with a velocity υ=qBwm, where w is the width of each region of the magnetic field. The time taken by the particle to come out of the region of the magnetic field is
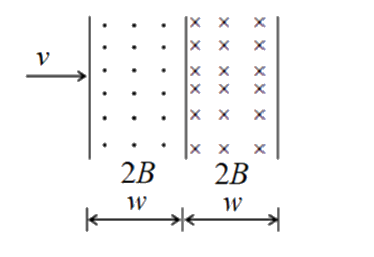 View Solution
View SolutionIn a certain region, uniform electric field E=−E0ˆk and magnetic field B=B0ˆk are present. At time t=0, a particle of mass m and charge q is given a velocity v=vj+vk. Find the minimum speed of the particle and the time when it happens so.
 View Solution
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then
 View Solution
View SolutionA particle of mass m and charge q is projected into a region having a perpendicular magnetic field B. Find the angle of deviation fo the particle as it comes out of the magnetic field if the width d of the regions is very smaller then
 View Solution
View SolutionThere exist uniform magnetic field →B=−B0ˆk in region of space with 0<x<d and 2d<x<3d as shown in the figure. A positive charged particle of mass m and charge q is projected with velocity →v=vˆi as shown in the figure. If radius of curvature of path of the charged particle in magnetic field isR(2d<R<3d) then time elapse by charged particle in magnetic field regions is
 View Solution
View SolutionA particle of mass m having a charge q enters into a circular region of radius R with velocity v directed towards the centre. The strength of magnetic field is B. Find the deviation in the path of the particle.
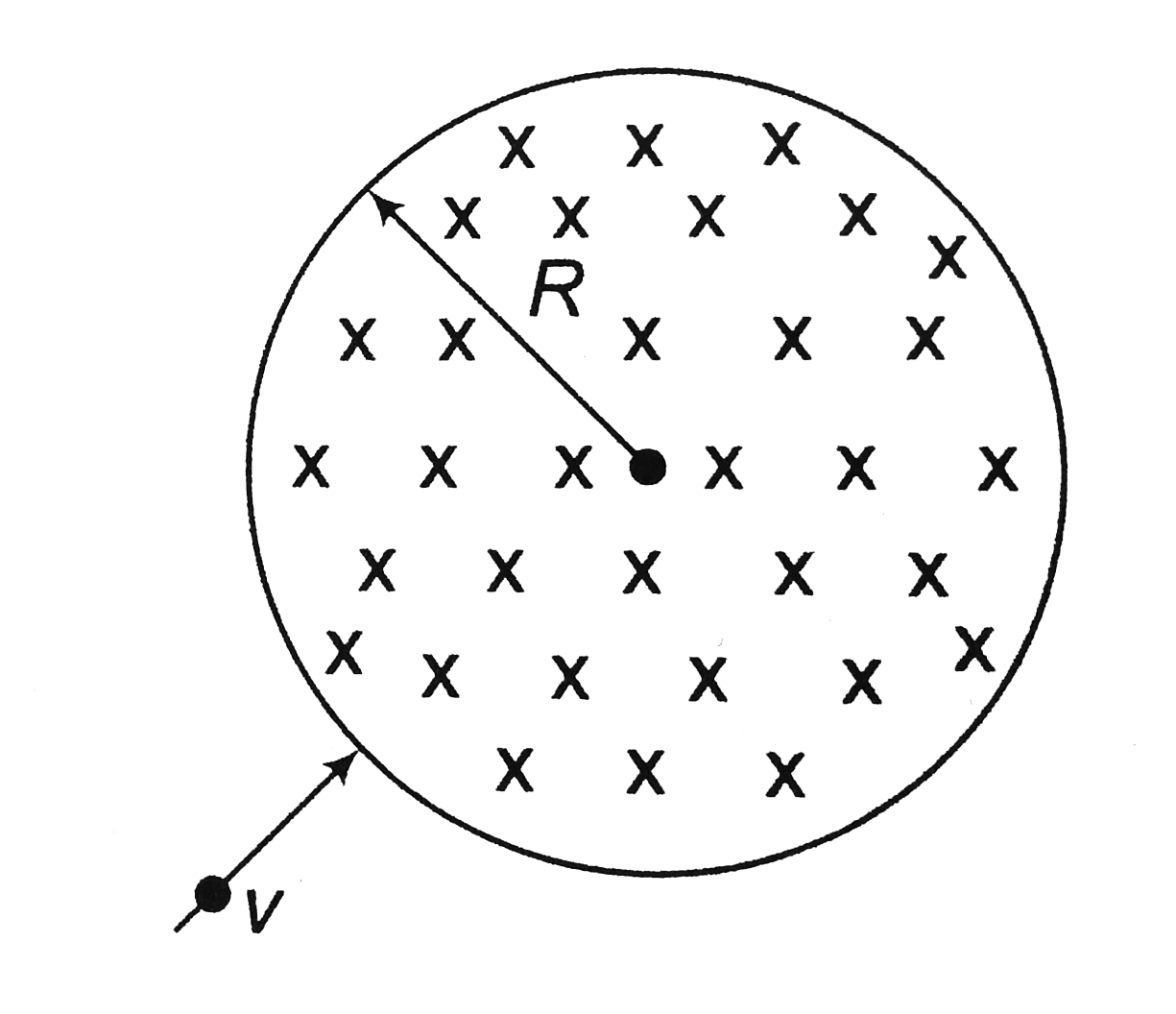 View Solution
View Solution

