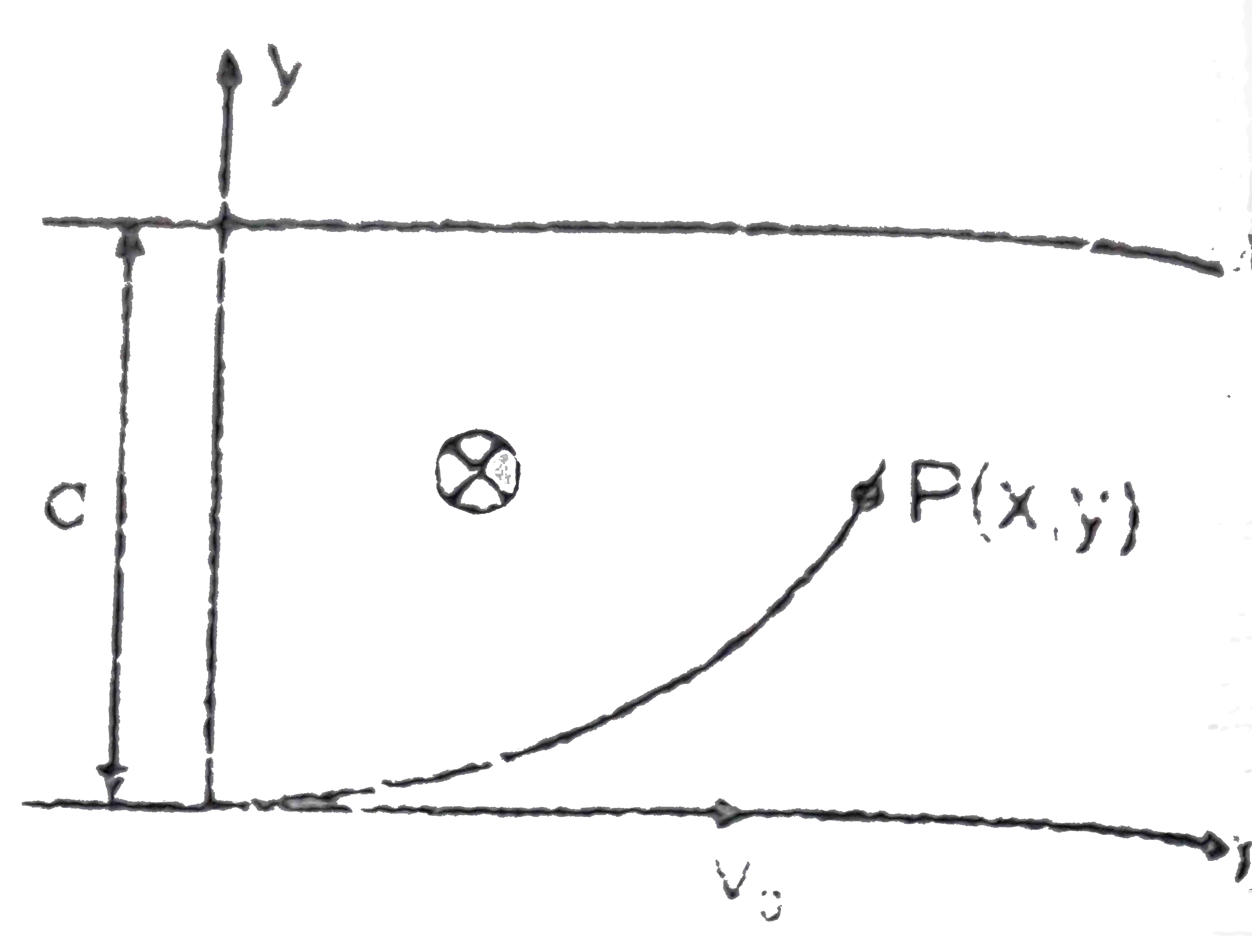
A non-uniform magnetic field $\to B = B_{0} (1 + \frac{y}{d}) (- ˆ k)$ is present in region of space in between $y = 0 & y = d$ .The lines are shown in the diagram.A particle of mass $m$ and positive charge $q$ is moving.Given an initial velocity $\to v = v_{0} ˆ i$ .Find the components of velocity of the particle when it leaves the field.

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $V_{x} = V_{0} - \frac{3 q B_{0} d}{2 m}$ and $V_{y} = {\sqrt{V_{0}^{2} - (V_{0} - \frac{3 q B_{0}}{2 m} d)}}^{2}$

Let at time $t$ particle be at point $P (x, y)$ and its velocity be
$\to B = (V_{x} ˆ i + V_{y} ˆ j)$
$∣ ∣ \to V ∣ ∣ = ∣ ∣ {\to V}_{0} ∣ ∣ \Rightarrow V_{0}^{2} = V_{x}^{2} + V_{y}^{2}$
(work done by magnetic field is always zero so charge in magnitude of velocity)Then, magnetic force on the particle at point $P$ is
$\to F = q (V_{x} ˆ i + V_{y} ˆ j) . B_{0} (1 + \frac{y}{d}) (- ˆ k) \Rightarrow - q B_{0} [1 + \frac{y}{d}] d y = m d v_{x}$
Now when the particle will be coming out of the at that point $y = d$ .Let the velocity in $x$ -direction be $V_{x}$ then integrating we get,
$V_{x} \int V_{0} d v_{x} = - \frac{q B_{0}}{m} d \int 0 d y = - \frac{q B_{0}}{m} [d + \frac{d^{2}}{2 d}] = - \frac{3 q B_{0} d}{2 m}$
so $V_{x} = V_{0} - \frac{3 q B_{0} d}{2 m}$
$\Rightarrow V_{y} = \sqrt{V_{0}^{2} - V_{x}^{2}}$
$\Rightarrow V_{y} = {\sqrt{V_{0}^{2} - (V_{0} - \frac{3 q B_{0}}{2 m} d)}}^{2}$

|

Updated on:21/07/2023

Class 12 PHYSICS ELECTROMAGNETIC INDUCTION

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
An electron is moving with an initial velocity $\to v = v_{0} ˆ i$ and is in a magnetic field $\to B = B_{0} ˆ j$ . Then it's de-Broglie wavelength
Aremains constant
Bincreases with time
Cdecreases with time
Dincreases and decreases periodically

RESONANCE ENGLISH-ELECTRODYNAMICS-Advanced level problems

Home
Ask Doubt
Profile