Two stars of masses 3×1031 kg each, and at distance 2×1011 m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star's rotation plane. In order to escape from the gravitational field of this double star, the minimum speed that meteorite should have at O is (Take Graviational constant G=6.67×10−11Nm2kg−2)
24×104m/s
1.4×105m/s
3.8×104m/s
2.8×105m/s
To solve the problem, we need to find the minimum speed that a meteorite must have at the center of mass (O) of a double star system in order to escape their gravitational field.
1. Identify the Given Values:
- Mass of each star, M=3×1031 kg
- Distance between the stars, d=2×1011 m
- Gravitational constant, G=6.67×10−11Nm2/kg2
2. Calculate the Distance from the Center of Mass to Each Star:
Since the stars are identical and the distance between them is d, the distance from the center of mass (O) to each star is:
r=d2=2×10112=1×1011m
3. Use Conservation of Energy:
The gravitational potential energy (U) between the meteorite (mass m) and each star is given by:
U=−GMmr
Since there are two stars, the total potential energy (U_total) when the meteorite is at O is:
Utotal=−GMmr−GMmr=−2GMmr
4. Set Up the Energy Conservation Equation:
At the point O, the total mechanical energy (E) of the meteorite is the sum of its kinetic energy (K) and potential energy (U):
K+Utotal=0
The kinetic energy (K) of the meteorite is given by:
K=12mv2
Therefore, we can write:
12mv2−2GMmr=0
5. Solve for the Minimum Speed (v):
Rearranging the equation gives:
12mv2=2GMmr
Dividing both sides by m (assuming m≠0):
12v2=2GMr
Multiplying both sides by 2:
v2=4GMr
Taking the square root:
v=√4GMr
6. Substituting the Values:
Substitute G=6.67×10−11Nm2/kg2, M=3×1031kg, and r=1×1011m:
v=√4×6.67×10−11×3×10311×1011
7. Calculating the Value:
v=√4×6.67×3×10201=√80.04×1020=√8.004×1021≈2.83×1010m/s
After calculation, we find:
v≈2.8×105m/s
Final Answer:
The minimum speed that the meteorite should have at O to escape the gravitational field of the double star system is approximately:
2.8×105m/s
- Mass of each star, M=3×1031 kg
- Distance between the stars, d=2×1011 m
- Gravitational constant, G=6.67×10−11Nm2/kg2
Since the stars are identical and the distance between them is d, the distance from the center of mass (O) to each star is:
r=d2=2×10112=1×1011m
The gravitational potential energy (U) between the meteorite (mass m) and each star is given by:
U=−GMmr
Since there are two stars, the total potential energy (U_total) when the meteorite is at O is:
Utotal=−GMmr−GMmr=−2GMmr
At the point O, the total mechanical energy (E) of the meteorite is the sum of its kinetic energy (K) and potential energy (U):
K+Utotal=0
The kinetic energy (K) of the meteorite is given by:
K=12mv2
Therefore, we can write:
12mv2−2GMmr=0
Rearranging the equation gives:
12mv2=2GMmr
Dividing both sides by m (assuming m≠0):
12v2=2GMr
Multiplying both sides by 2:
v2=4GMr
Taking the square root:
v=√4GMr
Substitute G=6.67×10−11Nm2/kg2, M=3×1031kg, and r=1×1011m:
v=√4×6.67×10−11×3×10311×1011
v=√4×6.67×3×10201=√80.04×1020=√8.004×1021≈2.83×1010m/s
After calculation, we find:
v≈2.8×105m/s
The minimum speed that the meteorite should have at O to escape the gravitational field of the double star system is approximately:
2.8×105m/s
Topper's Solved these Questions
Similar Questions
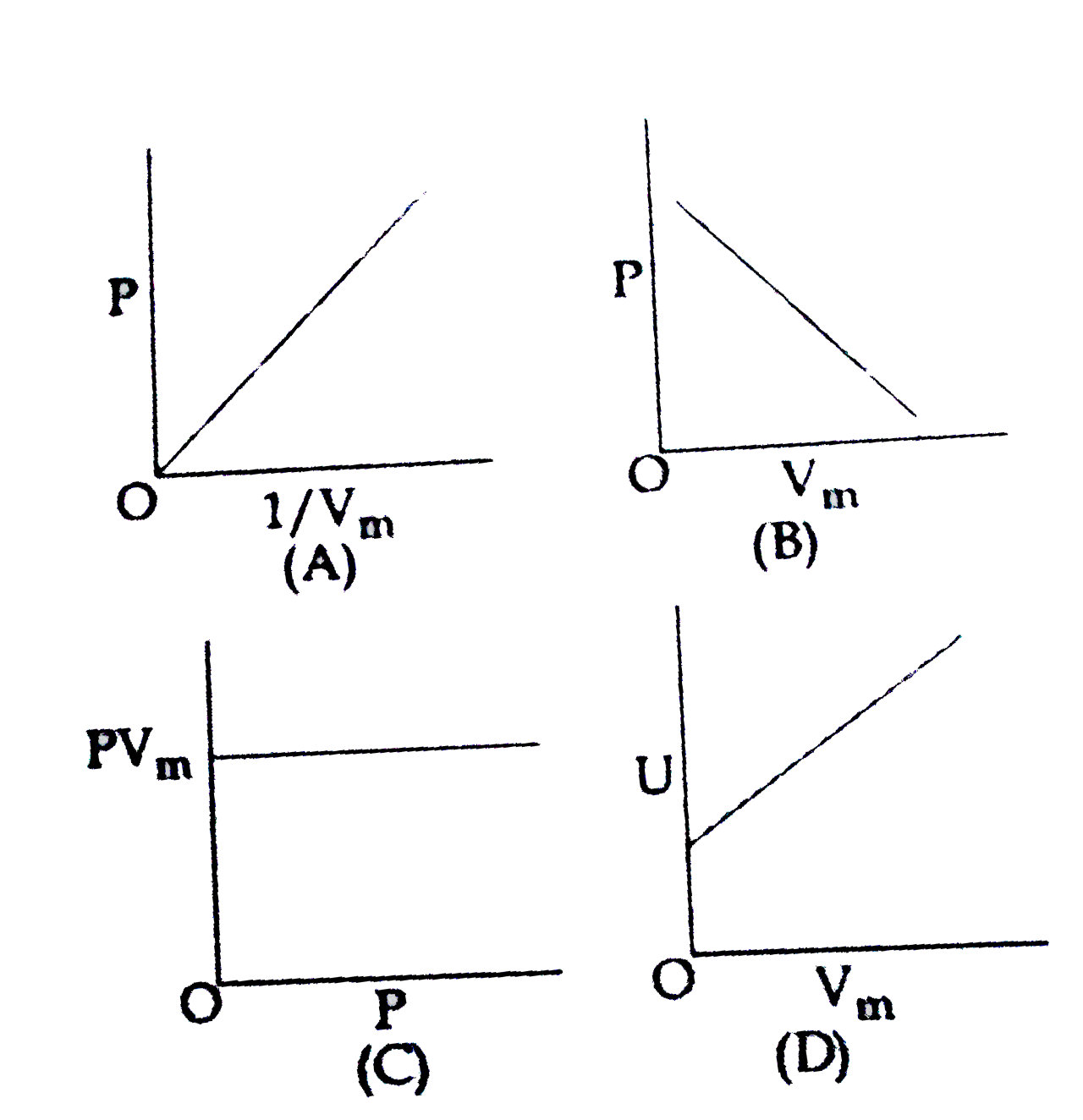
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionThe distance between the moon and earth is 3.8×108m. Find the gravitional potential at the mid point of the joining them. Given that the mass of the earth is 6×1024kg, mass of moon =7.4×1022kg and G=6.67×1011Nm2kg−2.
View SolutionThe distance between earth and moon is 3.8×108m. Determine the gravitational potential energy of earth-moon system. Given, mass of the earth =6×1024kg, mass of moon =7.4×1022kg and G=6.67×10−11Nm2kg−2
View SolutionCalculate the gravitational potential energy of a body of mass 30 kg , at a height of 4 R from the surface of Earth, where R (= 6.4 xx 10^(6) m) is the radius of the Earth. Mass of the Earth = 6.0 xx 10^(24) kg, G = 6.67 xx 10^(-11) Nm^(2) kg^(-2) .
View SolutionTwo stars of masses 3 xx 10^(31) kg each, and at distance 2 xx 10^(11) m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star's rotation plane. In order to escape from the gravitational field of this double star, the minimum speed that meteorite should have at O is (Take Graviational constant G = 6.67 xx 10^(-11) Nm^(2) kg^(-2) )
View SolutionCalculate the mass and density of the earth. Given that Gravitational constant G=6.67×10−11Nm2/kg2, the radius of the earth =6.37×106m and g =9.8m/s2.
View Solutionदो तारे, जिनमे प्रत्येक का द्रव्यमान 3×1031kg है तथा उनके बीच की दूरी 2×1011m है, अपने उभयनिष्ठ द्रव्यमान केन्द्र O के परितः किसी समतल में घूम रहे है। एक उल्का पिण्ड O से उनके घूर्णन समतल के लम्बवत दिशा से गुजरता है। इन दो तारो के गुरुत्वाकर्षण से पलायन करने के लिए उल्का पिण्ड की बिन्दु O पर न्यूनतम गति का मान होगा
(सार्वत्रिक गुरुत्वाकर्षण नियतांक, G=6.67×10−11N−m2kg−2)
View SolutionTwo stars of masses 3×10^31kg each, and at distance 2×10^11m rotate in a plane about their common centre of mass O. A meteorite passes through O moving perpendicular to the star's rotation plane. In order to escape from the gravitational field of this double star, the minimum speed that meteorite should have at O is : (Take Gravitational constant G=6.67×10^−11Nm^2kg^−2 )
View SolutionCalculate the force of attraction between two balls each of mass 10kg when their centres are 10 cm apart. The value of gravitational constant G=6.67×10−11Nm2kg−2
View SolutionIn a double star system two stars of masses m1 and m2 seperated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionA double star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses m and 2m and let their separation be 1. Their time period of rotation about their centre of mass will be proportional to (a) 1^(3//2) , (b)a , (c) m ,(d) m^(-1//2)
View SolutionIn a double star system two stars of masses m1andm2 separated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionA double star is a system of two stars rotating about their centre of mass only under their mutual gravitational attraction. Let the stars have masses m and 2m and let their separation be 1. Their time period of rotation about their centre of mass will be proportional to a) 1^(3//2) b) a c) m d) m^(-1//2)
View Solution
