In a particular double star system two stars of mass 3×1030 kg each revolve about their common centre of mass 1×1011 m on away.
(i). Calculate their common period of revolution
(ii). Suppose that a meteoroid (small solid particle in space) passes through this centre of mass moving at right angles to the orbital plane of the stars. What must its speed be if it is to escape from the gravitational field of the double star?Solution in Gujrati
The correct Answer is:(i). T=4π√r3Gm
(ii). v=√4Gmr,r=d2
(i) Necessary centripetal force=gravitational force
⇒ω2r=GM24r2⇒T=4π√r3GM
(iii). COME: KE+PE=0
⇒12mv2−2GMmr=0⇒v=√4GMr,(r=d2)
Topper's Solved these Questions
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 A (Previous Year Questions)
26 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 5 B (Previous Year Questions)
9 Videos
- GRAVITATIONBOOK - ALLEN CHAPTER - GRAVITATIONEXERCISE - Exercise 4 A (Conceptual Subjective Exercise)
14 Videos
- GEOMETRICAL OPTICSBOOK - ALLEN CHAPTER - GEOMETRICAL OPTICSEXERCISE - subjective
14 Videos
- KINEMATICS-2DBOOK - ALLEN CHAPTER - KINEMATICS-2DEXERCISE - Exercise (O-2)
47 Videos
Similar Questions
If suddenly the gravitational force of attraction between earth and satellite revolving around it becomes zero, then the satellite will
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View Solution_E01_076_Q01.png)
In the given figure L=1 metre if total gravitational force on 4 kg mass is →F1 and on 2 kg mass is →F2 then find out the ratio of ∣∣∣→F1→F2∣∣∣
View SolutionA prism of refractive index n1 & another prism of reactive index n2 are stuck together without a gap as shown in the figure.The angle of the prisms are as shown. n1&n2depend onλ,the wavelength of light according to n1=1.20+10.8×104λ2&n2=1.45+1.80×104λ2 where λ is in nm.

(i)Calculate the wavelength λ0for which rays incident at any angle on the interfaceBCpass through without bending at that interface.
(ii) for light of wavelength λ0,find the angle of incidencei on faceACsuch that the deviation produced by the combination of prism is minimum.
View SolutionA particle is moving in xy-plane .At certain instant the components of its velocity and acceleration are as follows ux=3m/s,uy=4m/s,ax=2m/s2anday=1m/s2. The rate of change of speed at this moment is
View SolutionA pair of stars rotates about a common centre of mass. One of the stars has a mass M and the other m . Their centres are a distance d apart, d being large compared to the size of either star. Derive an expression for the period of revolution of the stars about their common centre of mass. Compare their angular momenta and kinetic energies.
View SolutionIn a double star system, two stars of masses m_1 and m_2 separated by a distance x rotate about their centre of mass. Find the common angular velocity and Time period of revolution.
View Solution_S01_033_Q01.png)
A triple star ststem consists of two stars each of mass m in the same circular orbit about central star with mass M=2×1033kg. The two outer stars always lie at opposite ends of a diameter of their common circular orbit the radius of the circular orbit is r=1011 m and the orbital period each star is 1.6×107s [take π2=10 and G=203×10−11Mn2kg−2]
Q. The mass m of the outer stars is:
View SolutionIn a binary star system one star has thrice the mass of other. The stars rotate about their common centre of mass then :
View SolutionA system consists of two stars of equal masses that revolve in a circular orbit about their centre of mass . Orbital speed of each star is v and period is T . Find the mass M of each star . (G is gravitational constant )
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M=2m The distance between the centres of the stars is d (d being large compared to the size of either star) .
The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View SolutionA pair of stars rotates about their centre of mass One of the stars has a mass M and the other has mass m such that M =2m The distance between the centres of the stars is d (d being large compared to the size of either star) . The period of rotation of the stars about their common centre of mass (in time of d ,m ,G) is .
View SolutionA certain triple-star system consists of two stars, each of mass m, revolving about a central star, mass M, in the same circular orbit. The two stars stay at opposite ends of a diameter of the circular orbit, see figure. Derive an expression for the period of revolution of the stars, the radius of the orbit is r.
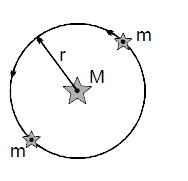
View SolutionIn a double star system two stars of masses m1 and m2 seperated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View SolutionIn a double star system, two stars of masses m_(1) and m_2 seperated by a distance d rotate about their centre of mass. Then their common angular velocity would be:
View SolutionIn a double star system two stars of masses m1andm2 separated by a distance .d. rotates about their centre of mass. Then the common angular velocity and time period is
View Solution
