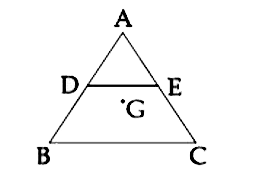
An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I0 If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then :

I=1516I0
I=34I0
I=916I0
I=I04
Step by step video & image solution for An equilateral triangle ABC is cut from a thin solid sheet of wood .(see figure ) D,E and F are the mid-points of its sides as shown and G is the centre of the triangle.The moment of inertia of the triangle about an axis passing through G and perpendicular to the plane to the triangle is I_(0) If the smaller triangle DEF is removed from ABC , the moment of inertia of the remaining figure about the same axis is I. Then : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
D,E and F are the middle points of the sides of the triangle ABC, then
View SolutionABC is a plane lamina of the shape of an equilateral triangle. D , E are mid points of AB,AC and G is the centroid of the lamina . Moment of inertia of the lamina about an axis passing through G and perpendicular to the plane ABC is I0 If part ADE is removed, the moment of inertia of a remaining part about the same axis is NI016 where N is an integer . Value of N is
View SolutionThree identical rods are joined together to form an equilateral triangle frame. Its radius of gyration about an axis passing through a corner and perpendicular to the plane of the triangle is.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
BDEF is a parallelogram.
View SolutionThe moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
View SolutionIf D, E and F are the mid-points of the sides of a △ABC , the ratio of the areas of the triangles DEF and ABC is .......
View SolutionA rod of mass 3 kg and of length 3m is bent in the form of an equilateral triangle. The moment of inertia of the triangle about a vertical axis perpendicular to plane and passing through centre of mass is

View SolutionD, E and F are the mid-points of the sides BC, CA and AB respectively of triangle ABC. Prove that:
area of BDEF is half the area of ΔABC.
View Solution
Three rods each of mass m and length l are joined together to form an equilateral triangle as shown in figure. Find the moment of inertial of the system about an axis passing through its centre of mass and perpendicular to the plane of the particle.
View Solution
