The moment of inertia of a thin uniform rod about an axis passing through its centre and perpendicular to its length is I0. What is the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod ?
12I0
3I0
5I0
4I0
To find the moment of inertia of a thin uniform rod about an axis passing through one end and perpendicular to the rod, we can use the parallel axis theorem. Let's go through the solution step by step.
Step 1: Understand the given information
The moment of inertia of a thin uniform rod about an axis passing through its center and perpendicular to its length is given as I0.
Step 2: Recall the formula for moment of inertia
For a thin uniform rod of mass m and length l, the moment of inertia about an axis through its center is given by:
I0=ml212
Step 3: Use the parallel axis theorem
The parallel axis theorem states that if you know the moment of inertia about an axis through the center of mass (CM), you can find the moment of inertia about any parallel axis by adding md2, where d is the distance between the two axes.
Step 4: Calculate the distance d
In this case, we want to find the moment of inertia about an axis at one end of the rod. The distance d from the center of the rod to one end is:
d=l2
Step 5: Apply the parallel axis theorem
The moment of inertia about the end of the rod (I1) can be calculated as:
I1=I0+md2
Substituting the values:
I1=I0+m(l2)2
I1=I0+ml24
Step 6: Substitute I0 into the equation
Now, substituting I0=ml212:
I1=ml212+ml24
Step 7: Find a common denominator and simplify
To add these fractions, we need a common denominator:
I1=ml212+3ml212=ml2+3ml212=4ml212=ml23
Step 8: Relate I1 to I0
Now, we can express I1 in terms of I0:
I1=4I0
Conclusion
Thus, the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod is:
I1=4I0
The moment of inertia of a thin uniform rod about an axis passing through its center and perpendicular to its length is given as I0.
For a thin uniform rod of mass m and length l, the moment of inertia about an axis through its center is given by:
I0=ml212
The parallel axis theorem states that if you know the moment of inertia about an axis through the center of mass (CM), you can find the moment of inertia about any parallel axis by adding md2, where d is the distance between the two axes.
In this case, we want to find the moment of inertia about an axis at one end of the rod. The distance d from the center of the rod to one end is:
d=l2
The moment of inertia about the end of the rod (I1) can be calculated as:
I1=I0+md2
Substituting the values:
I1=I0+m(l2)2
I1=I0+ml24
Now, substituting I0=ml212:
I1=ml212+ml24
To add these fractions, we need a common denominator:
I1=ml212+3ml212=ml2+3ml212=4ml212=ml23
Now, we can express I1 in terms of I0:
I1=4I0
Thus, the moment of inertia of the rod about an axis passing through one end and perpendicular to the rod is:
I1=4I0
Topper's Solved these Questions
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - B) Objective Type Questions (One option is correct)
60 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
29 Videos
- SYSTEM OF PARTICLES AND ROTATIONAL MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SYSTEM OF PARTICLES AND ROTATIONAL MOTIONEXERCISE - Illustration
4 Videos
- SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEMICONDUCTOR ELECTRONICS: MATERIALS, DEVICES AND SIMPLE CIRCUITSEXERCISE - Assignment (Section-D (Assertion and reason))
5 Videos
- TEST 1BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST 1EXERCISE - EXERCISE
21 Videos
Similar Questions
The moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View SolutionThe moment of inertia of a uniform ring about an axis passing through its centre and perpendicular to its plane is 100kgm2. What is the moment of inertia of the ring about its diameter ?
View Solution
Knowledge Check
The radius of gyration of an uniform rod of length l about an axis passing through one of its ends and perpendicular to its length is.
Al√2Bl3Cl√3Dl2
The moment of inertia of a copper disc, rotating about an axis passing through its centre and perpendicular to its plane
View SolutionThe moment of inertia of a thin uniform rod of mass M and length L about an axis passing through its mid-point and perpendicular to its length isI0. Its moment of inertia about an axis passing through one of its ends perpendicular to its length is.
View SolutionMoment of inertia of a ring of mass M and radius R about an axis passing through the centre and perpendicular to the plane is
View SolutionFigure shows the variation of the moment of inertia of a uniform rod, about an axis passing through itss centre and inclined at an angle θ to the length. The moment of inertia of the rod about an axis passing through one of its ends and making an angle θ=π3 will be
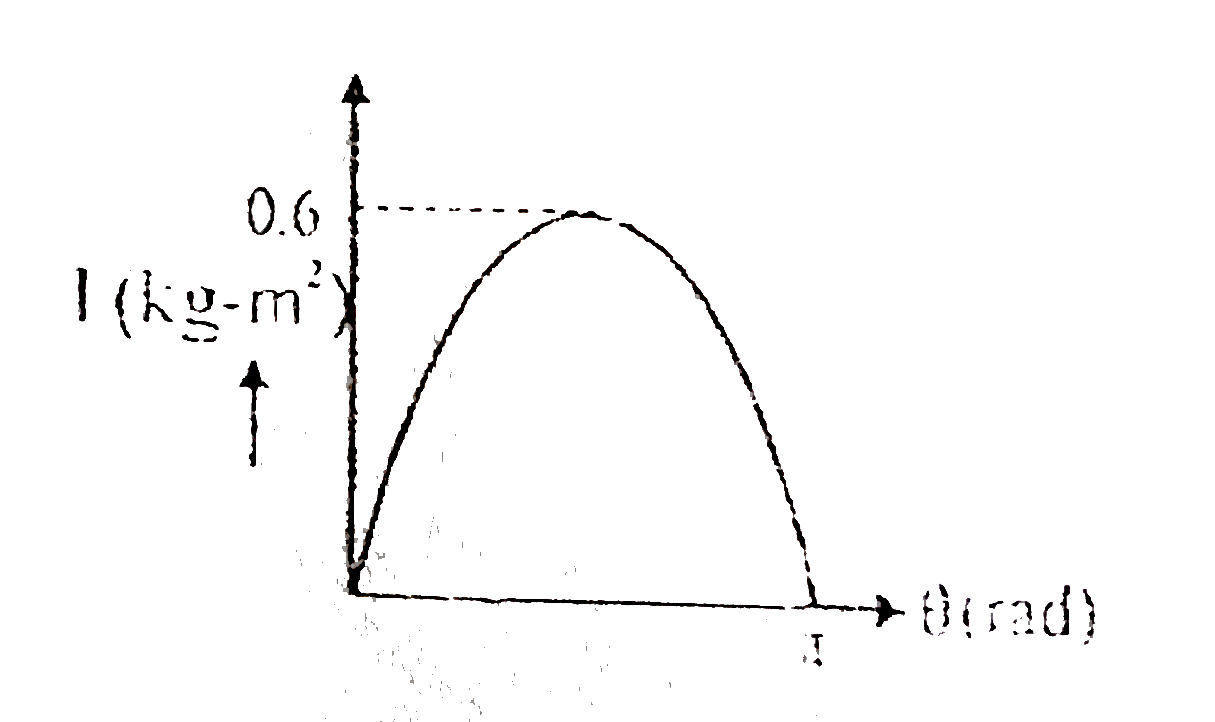
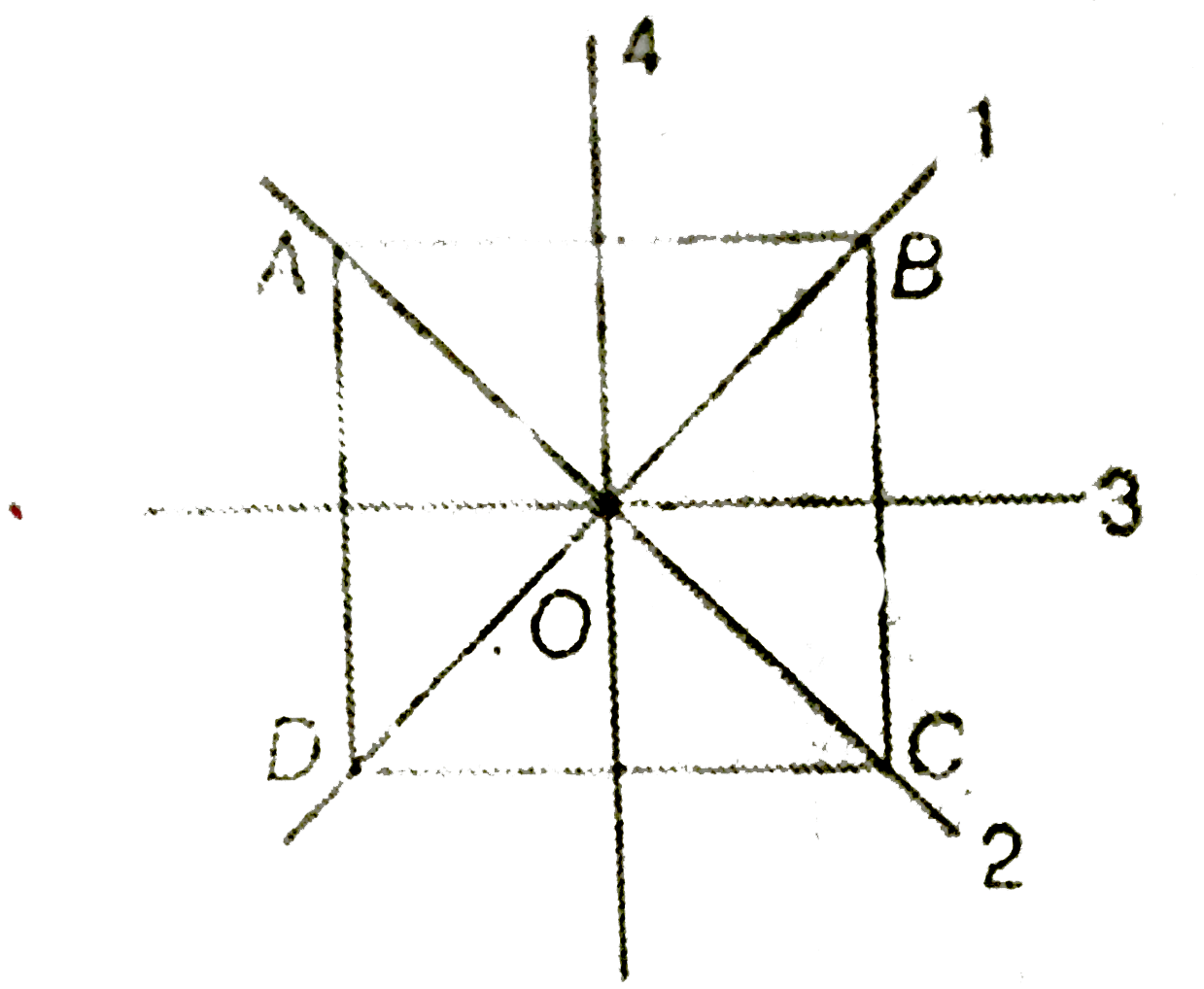
View SolutionThe moment of inertia of a thin square plate ABCD of uniform thickness about an axis passing through the centre O and perpendicular to plate is
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View SolutionCalculate the moment of inertia of a ring of mass 2kg and radius 2cm about an axis passing through its centre and perpendicular to its surface.
View Solution
