A particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
10√3m/s
Zero
10√2m/s
10m/s
To solve the problem, we need to find the magnitude of the change in velocity of a particle moving in a circular path when it moves through an angle of 60∘. Here’s the step-by-step solution:
Step 1: Understand the initial and final velocity vectors
- The particle is moving with a constant speed of 10m/s.
- Initially, let’s denote the velocity vector at point A (initial position) as →V1.
- After moving through an angle of 60∘, the particle reaches point B, where the velocity vector is denoted as →V2.
Step 2: Determine the angle between the velocity vectors
- The angle between the two velocity vectors →V1 and →V2 is 60∘ because the particle moves through this angle along the circular path.
Step 3: Use the formula for the change in velocity
- The magnitude of the change in velocity |Δ→V| can be calculated using the formula for the resultant of two vectors:
|Δ→V|=|→V2−→V1|
- Since the magnitudes of both vectors are equal (both are 10m/s), we can use the cosine rule:
|Δ→V|=√|→V1|2+|→V2|2−2|→V1||→V2|cos(θ)
where θ=60∘.
Step 4: Substitute the values into the equation
- Substituting |→V1|=|→V2|=10m/s and θ=60∘:
|Δ→V|=√102+102−2⋅10⋅10⋅cos(60∘)
- We know that cos(60∘)=12:
|Δ→V|=√100+100−2⋅10⋅10⋅12
|Δ→V|=√100+100−100=√100=10m/s
Conclusion
- The magnitude of the change in velocity of the particle when it moves through an angle of 60∘ is 10m/s.
- The particle is moving with a constant speed of 10m/s.
- Initially, let’s denote the velocity vector at point A (initial position) as →V1.
- After moving through an angle of 60∘, the particle reaches point B, where the velocity vector is denoted as →V2.
- The angle between the two velocity vectors →V1 and →V2 is 60∘ because the particle moves through this angle along the circular path.
- The magnitude of the change in velocity |Δ→V| can be calculated using the formula for the resultant of two vectors:
|Δ→V|=|→V2−→V1|
- Since the magnitudes of both vectors are equal (both are 10m/s), we can use the cosine rule:
|Δ→V|=√|→V1|2+|→V2|2−2|→V1||→V2|cos(θ)
where θ=60∘.
- Substituting |→V1|=|→V2|=10m/s and θ=60∘:
|Δ→V|=√102+102−2⋅10⋅10⋅cos(60∘)
- We know that cos(60∘)=12:
|Δ→V|=√100+100−2⋅10⋅10⋅12
|Δ→V|=√100+100−100=√100=10m/s
- The magnitude of the change in velocity of the particle when it moves through an angle of 60∘ is 10m/s.
Topper's Solved these Questions
Similar Questions
A particle is moving on a circular path with constant speed v. The magnitude of the change in its velocity after it has described an angle of 90∘ is :
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
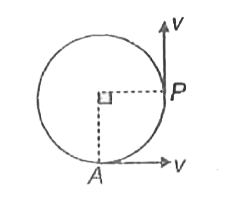
View Solution
Knowledge Check
A particle is moving on a circular path with a constant speed v. Its change of velocity as it moves from A to B is:
 A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A2vsin(2θ)BzeroC2vsin(θ2)D2vcos(θ2)
A particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA particle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
View SolutionA particle is moving in a circular orbit with constant speed. Select wrong alternate.
View SolutionA particle is moving on a circular path with constant speed v then the change in its velocity after it has described an angle of 60∘ will be
View SolutionA car is moving in a circular path with a uniform speed v. Find the magnitude of change in its velocity when the car rotates through an angle θ.
View SolutionA particle is moving along an elliptical path with constant speed. As it moves from A to B, magnitude of its acceleration :
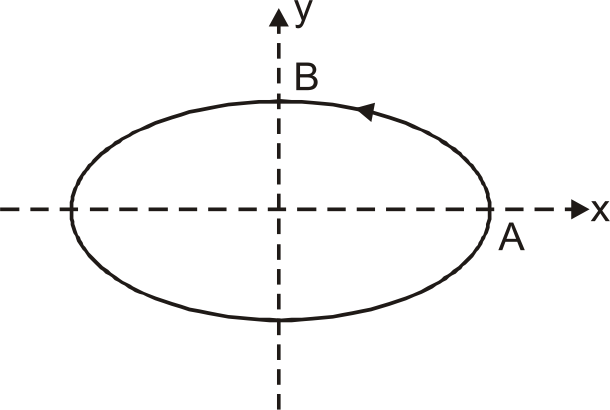
View Solution
