A particle is moving on a circular path of radius 10m with uniform speed of 4ms−1.The magnitude of change in velocity of particle when it completes a semi circular path is
4ms−1
8ms−1
10ms−1
zero
The correct Answer is:B
To solve the problem of finding the magnitude of change in velocity of a particle moving on a circular path when it completes a semi-circular path, we can follow these steps:
Step 1: Understand the Initial and Final Velocities
- The particle is moving in a circular path of radius r=10m with a uniform speed of v=4m/s.
- When the particle starts at point A (the top of the semicircle), its velocity is directed tangentially to the path. We can assume it is moving in the positive y-direction. Thus, the initial velocity →vA=4^jm/s.
Step 2: Determine the Final Velocity
- After completing a semi-circular path, the particle reaches point B (the bottom of the semicircle). At this point, the velocity is still 4m/s but directed tangentially in the negative y-direction. Thus, the final velocity →vB=−4^jm/s.
Step 3: Calculate the Change in Velocity
- The change in velocity Δ→v can be calculated as:
Δ→v=→vB−→vA
Substituting the values:
Δ→v=(−4^j)−(4^j)=−4^j−4^j=−8^jm/s
Step 4: Find the Magnitude of Change in Velocity
- The magnitude of the change in velocity is given by:
|Δ→v|=|Δv|=√(−8)2=√64=8m/s
Conclusion
- The magnitude of the change in velocity of the particle when it completes a semi-circular path is 8m/s.
- The particle is moving in a circular path of radius r=10m with a uniform speed of v=4m/s.
- When the particle starts at point A (the top of the semicircle), its velocity is directed tangentially to the path. We can assume it is moving in the positive y-direction. Thus, the initial velocity →vA=4^jm/s.
- After completing a semi-circular path, the particle reaches point B (the bottom of the semicircle). At this point, the velocity is still 4m/s but directed tangentially in the negative y-direction. Thus, the final velocity →vB=−4^jm/s.
- The change in velocity Δ→v can be calculated as:
Δ→v=→vB−→vA
Substituting the values:
Δ→v=(−4^j)−(4^j)=−4^j−4^j=−8^jm/s
- The magnitude of the change in velocity is given by:
|Δ→v|=|Δv|=√(−8)2=√64=8m/s
- The magnitude of the change in velocity of the particle when it completes a semi-circular path is 8m/s.
Topper's Solved these Questions
Similar Questions
A particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA particle of mass 'm' is moving on a circular path of radius 'r' with uniform speed 'v'. Rate of change of linear momentum is
View SolutionA particle is moving on a circular track of radius 30 cm with a constant speed of 6ms−1. Its acceleration is
View SolutionA particle is moving along a circular path with a constant speed 10ms−1.What is the magnitude of the change in velocity of the particle ,when it moves through an angle of 60∘ around the center of the circle ?
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View SolutionA particle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle of mass 2 kg is moving in circular path with constant speed 20 m/s. The magnitude of change in velocity when particle travels from A to P will be
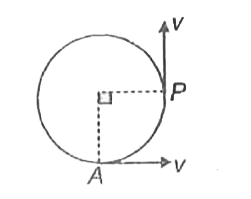
View SolutionA particle is moving along a circular path of radius 5 m with a uniform speed 5ms−1. What will be the average acceleration when the particle completes half revolution?
View SolutionA particle is moving along a circular path with uniform speed. Through what angle does its angular velocity change when it completes half of the circular path ?
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View Solution