A motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the starting point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (Speed of sound = 330ms−2)
49 m
98 m
147 m
196 m
The correct Answer is:B
To solve the problem, we will follow these steps:
Step 1: Understand the problem
The motorcycle accelerates from rest at a rate of 2m/s2. We need to find the distance traveled by the motorcycle when the driver hears the frequency of the siren at 94% of its original value.
Step 2: Set up the frequency equation
The apparent frequency f′ heard by the observer (motorcycle driver) moving away from the stationary source (siren) can be expressed using the Doppler effect formula:
f′=f0(v−vov)
where:
- f0 is the original frequency of the siren,
- v is the speed of sound (330m/s),
- vo is the speed of the observer (motorcycle).
Step 3: Set the equation for 94% of the original frequency
We want the apparent frequency to be 94% of the original frequency:
f′=0.94f0
Substituting this into the frequency equation gives:
0.94f0=f0(v−vov)
Step 4: Simplify the equation
Dividing both sides by f0 (assuming f0≠0):
0.94=v−vov
Rearranging gives:
0.94v=v−vo
vo=v−0.94v=0.06v
Step 5: Calculate the speed of the observer
Substituting v=330m/s:
vo=0.06×330=19.8m/s
Step 6: Use kinematics to find the distance traveled
Using the third equation of motion:
vo=u+at
where u=0 (initial velocity), a=2m/s2, and t is the time taken. We can rearrange this to find t:
t=voa=19.82=9.9s
Step 7: Calculate the distance traveled
Using the formula for distance:
s=ut+12at2
Substituting u=0:
s=12⋅2⋅(9.9)2
s=1⋅98.01=98.01m
Final Result
The motorcycle has traveled approximately 98m when the driver hears the frequency of the siren at 94% of its original value.
---
The motorcycle accelerates from rest at a rate of 2m/s2. We need to find the distance traveled by the motorcycle when the driver hears the frequency of the siren at 94% of its original value.
The apparent frequency f′ heard by the observer (motorcycle driver) moving away from the stationary source (siren) can be expressed using the Doppler effect formula:
f′=f0(v−vov)
where:
- f0 is the original frequency of the siren,
- v is the speed of sound (330m/s),
- vo is the speed of the observer (motorcycle).
We want the apparent frequency to be 94% of the original frequency:
f′=0.94f0
Substituting this into the frequency equation gives:
0.94f0=f0(v−vov)
Dividing both sides by f0 (assuming f0≠0):
0.94=v−vov
Rearranging gives:
0.94v=v−vo
vo=v−0.94v=0.06v
Substituting v=330m/s:
vo=0.06×330=19.8m/s
Using the third equation of motion:
vo=u+at
where u=0 (initial velocity), a=2m/s2, and t is the time taken. We can rearrange this to find t:
t=voa=19.82=9.9s
Using the formula for distance:
s=ut+12at2
Substituting u=0:
s=12⋅2⋅(9.9)2
s=1⋅98.01=98.01m
The motorcycle has traveled approximately 98m when the driver hears the frequency of the siren at 94% of its original value.
Topper's Solved these Questions
Similar Questions
A motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the straight point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was al rest? (Speed of sound = 330ms−1)
View SolutionA motorcycle starts from rest and accelerates along a straight line at 2.2ms2. The speed of sound is 330ms. A siren at the starting point remains stationary. When the driver hears the frequency of the siren at 90% of when motorcycle is stationary, the distance travelled by the motorcyclist is
View Solution
Knowledge Check
How long would it take a car, starting from rest and accelerating uniformly in a straight line at 5m/s2, to cover a distance of 200 m ?
A9.0 sB10.5 sC12.0 sD15.5 s
A motorcycle starts from rest and accelerates along a straight line at 2.2ms2. The speed of sound is 330ms. A siren at the starting point remains stationary. When the driver hears the frequency of the siren at 90% of when motorcycle is stationary, the distance travelled by the motorcyclist is
View SolutionA motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionA particle starts motion from rest and moves along a straight line. Its velocity-time graph is shown. Find out speed of particle at t=2s and at t=3s.

View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.

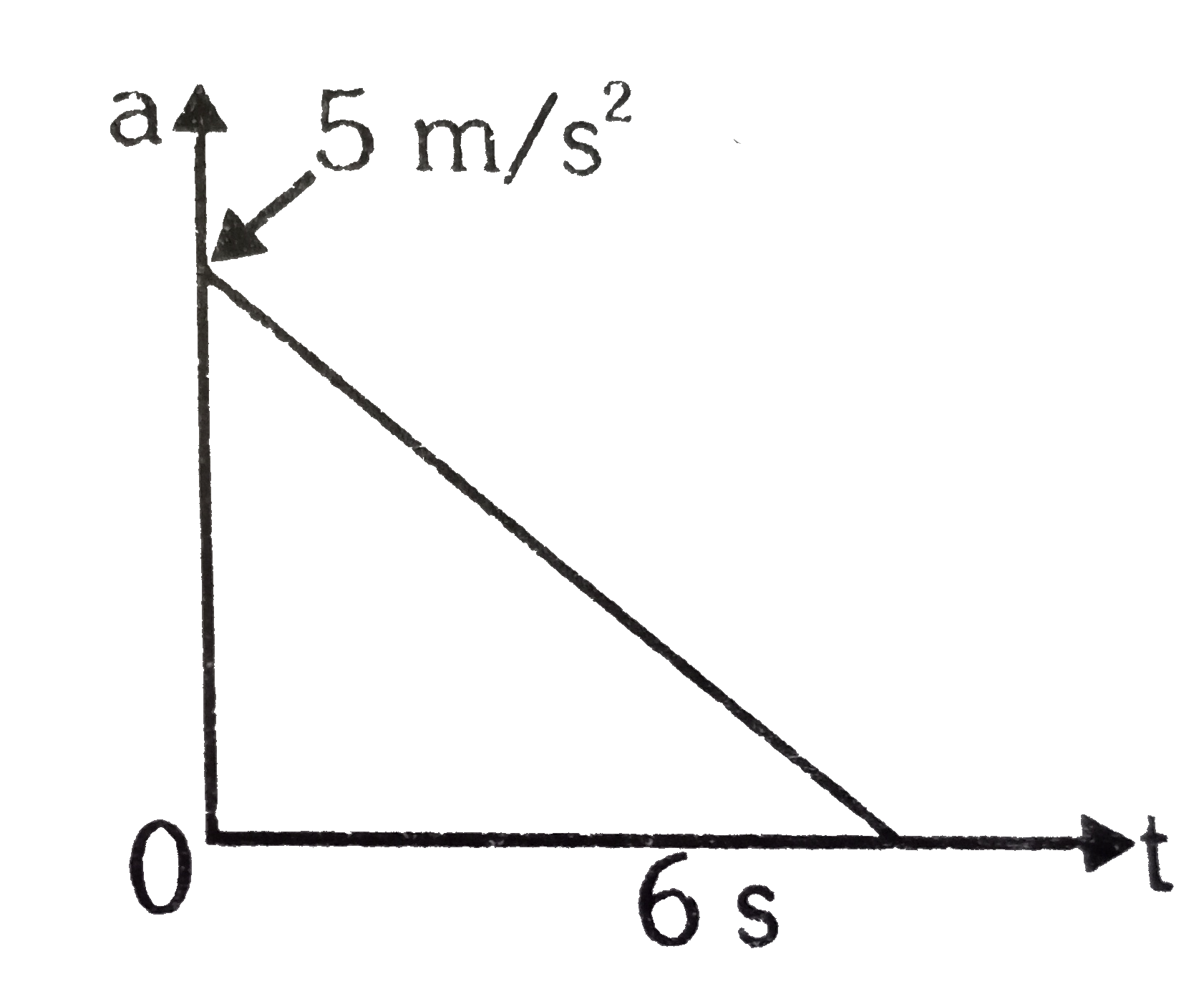
View SolutionA particle starts from rest. Its acceleration at time t=0 is 5m/s2 which varies with time as shown in the figure. The maximum speed of the particle will be
View SolutionA bus starts from rest with a constant acceleration of 5m/s2 at the same time a car travelling with a constant velocity 50m/s over takes and passes the bus. How fast is the bus travelling when they are side by side?
View SolutionA point initially at rest moves along x-axis. Its acceleration varies with time as a=(6t+5)m/s2. If it starts from origin, the distance covered in 2 s is:
View Solution
