A motorcycle starts from rest and accelerates along a straight line at 2.2ms2. The speed of sound is 330ms. A siren at the starting point remains stationary. When the driver hears the frequency of the siren at 90% of when motorcycle is stationary, the distance travelled by the motorcyclist is
123.75 m
247.5 m
495 m
990 m
The correct Answer is:B
To solve the problem step by step, we will follow the outlined reasoning from the video transcript:
Step 1: Understand the problem
We have a motorcycle that starts from rest and accelerates at a rate of 2.2m/s2. A siren is stationary at the starting point, and the motorcyclist hears the frequency of the siren at 90% of the frequency when stationary. We need to find the distance traveled by the motorcyclist when this happens.
Hint: Identify the key variables: acceleration, speed of sound, and the frequency heard by the motorcyclist.
Step 2: Set up the frequency relationship
Let f0 be the frequency of the siren when the motorcycle is stationary. The frequency heard by the motorcyclist when moving is given by the Doppler effect formula:
f′=f0V+VoV
Where:
- f′ is the apparent frequency heard by the observer (motorcyclist).
- V is the speed of sound (330m/s).
- Vo is the velocity of the observer (motorcyclist).
Since the motorcyclist hears the frequency at 90% of the stationary frequency:
f′=0.9f0
Substituting this into the Doppler effect equation gives:
0.9f0=f0V+VoV
Hint: Remember that the source is stationary, so Vs=0.
Step 3: Simplify the equation
Cancelling f0 from both sides (assuming f0≠0):
0.9=V+VoV
Rearranging gives:
0.9V=V+Vo
Vo=0.9V−V
Vo=−0.1V
Since V=330m/s:
Vo=−0.1×330=−33m/s
Hint: The negative sign indicates that the motorcycle is moving away from the source.
Step 4: Relate velocity to distance
The motorcyclist starts from rest and accelerates. We can use the kinematic equation:
V2=u2+2as
Where:
- V is the final velocity (33m/s).
- u is the initial velocity (0m/s).
- a is the acceleration (2.2m/s2).
- s is the distance traveled.
Substituting the known values:
(33)2=0+2⋅2.2⋅s
1089=4.4s
Hint: Rearranging this equation will help you find the distance s.
Step 5: Solve for distance
Now, solve for s:
s=10894.4
Calculating this gives:
s=247.5m
Hint: Ensure your calculations are correct and check the units.
Final Answer
The distance traveled by the motorcyclist is 247.5m.
We have a motorcycle that starts from rest and accelerates at a rate of 2.2m/s2. A siren is stationary at the starting point, and the motorcyclist hears the frequency of the siren at 90% of the frequency when stationary. We need to find the distance traveled by the motorcyclist when this happens.
Let f0 be the frequency of the siren when the motorcycle is stationary. The frequency heard by the motorcyclist when moving is given by the Doppler effect formula:
- f′ is the apparent frequency heard by the observer (motorcyclist).
- V is the speed of sound (330m/s).
- Vo is the velocity of the observer (motorcyclist).
Cancelling f0 from both sides (assuming f0≠0):
The motorcyclist starts from rest and accelerates. We can use the kinematic equation:
- V is the final velocity (33m/s).
- u is the initial velocity (0m/s).
- a is the acceleration (2.2m/s2).
- s is the distance traveled.
Now, solve for s:
The distance traveled by the motorcyclist is 247.5m.
Topper's Solved these Questions
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Multiple Correct44videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Assertion-Reasoning24videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SOUND WAVES AND DOPPLER EFFECTEXERCISE - Subjective56videos
SOUND WAVES AND DOPPLER EFFECT
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - RIGID BODY DYNAMICS 2EXERCISE - Interger2videos
RIGID BODY DYNAMICS 2
- BOOK - CENGAGE PHYSICS ENGLISHCHAPTER - SUPERPOSITION AND STANDING WAVESEXERCISE - Comprehension Type5videos
SUPERPOSITION AND STANDING WAVES
Similar Questions
A motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the starting point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (Speed of sound = 330ms−2)
View SolutionA motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the starting point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was at rest ? (Speed of sound = 330ms−2)
View Solution
Knowledge Check
- Question 1 - Select One
How long would it take a car, starting from rest and accelerating uniformly in a straight line at 5m/s2, to cover a distance of 200 m ?
A9.0 sB10.5 sC12.0 sD15.5 s
A motor cycle starts from rest and accelerates along a straight path at 2m/s2. At the straight point of the motor cycle there is a stationary electric siren. How far has the motor cycle gone when the driver hears the frequency of the siren at 94% of its value when the motor cycle was al rest? (Speed of sound = 330ms−1)
View SolutionA motorboat starting from rest on a lake accelerates in a straight line at a constant rate of 3.0m/s2 for 8.0s. How far does the boat travel during this time ?
View SolutionA body starts from rest and accelerates with 4m/s2 for 5 seconds. Find the distance travelled with 5 seconds.
View SolutionThe acceleration of a particle starting from rest and travelling along a straight line is shown in figure. The maximum speed of the particle is
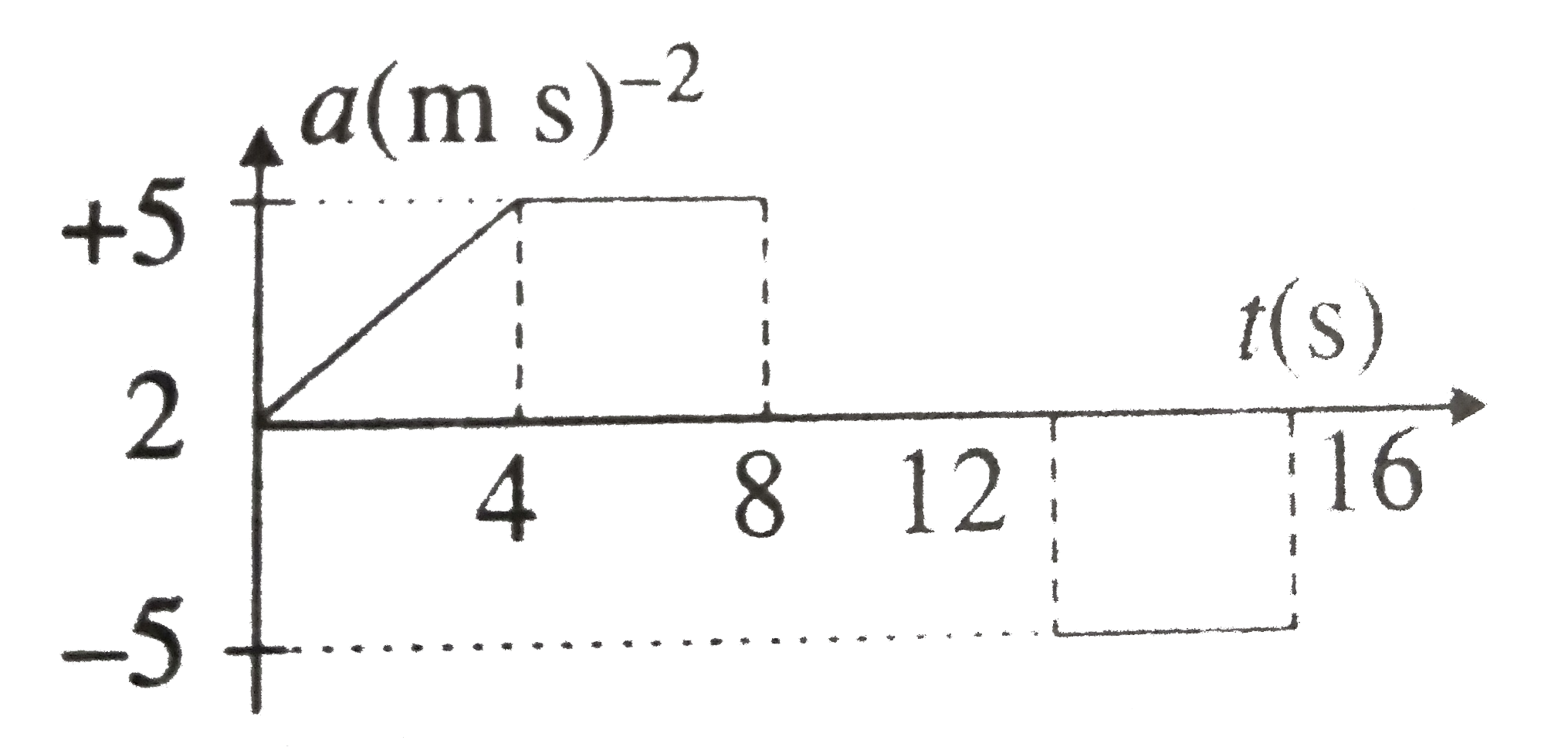 View Solution
View SolutionA particle starts motion from rest and moves along a straight line. Its acceleration-time graph is shown. Find out speed of particle at t=2s and at t=3s.
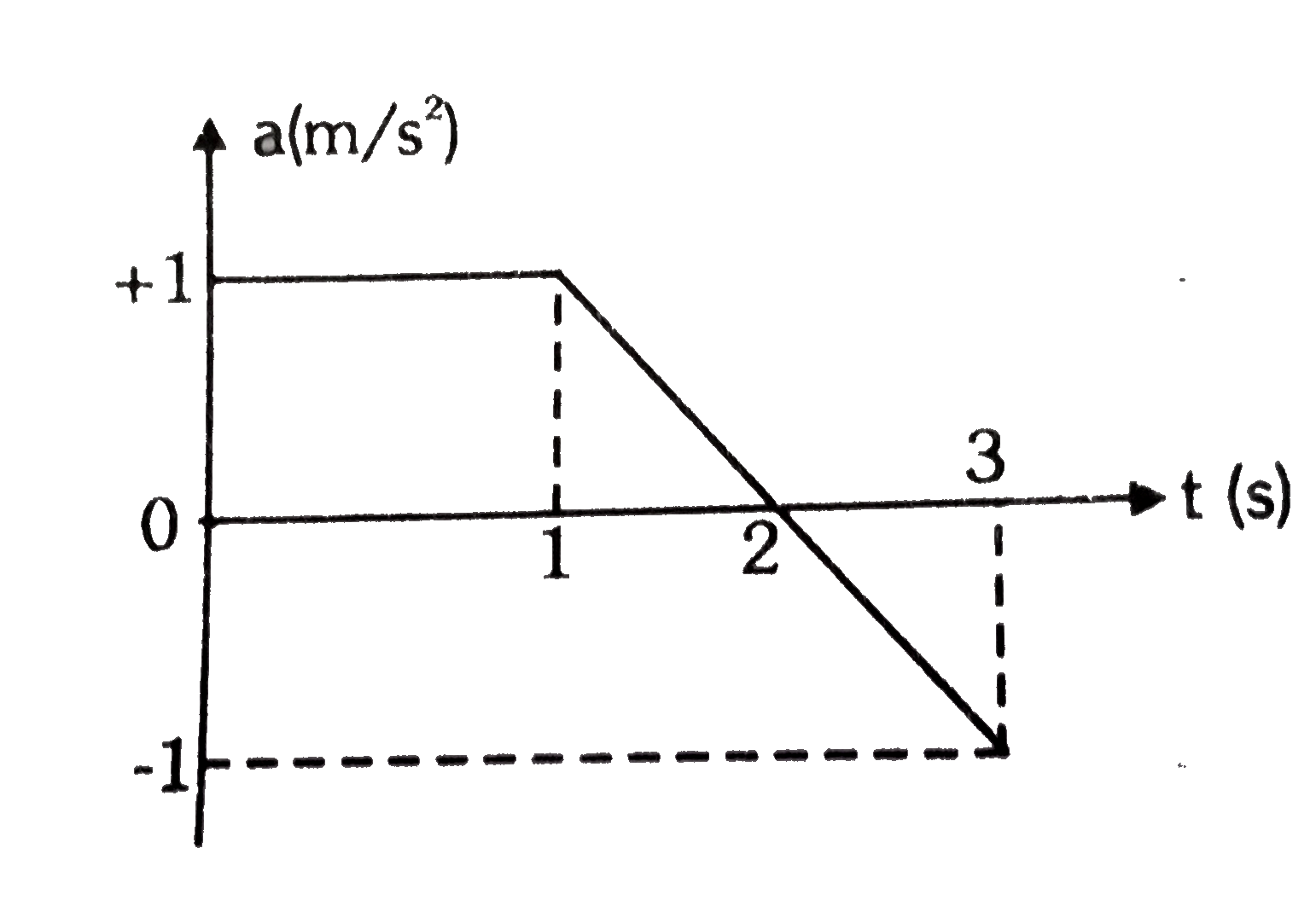 View Solution
View SolutionA bus starts from rest and moves whith acceleration a=2ms2. The ratio of the distance covered in 6th second to that covered in 6 seconds is
View SolutionA body starting from rest moves along a straight line with a constant acceleration. The variation of speed (v) with distance (s) is represented by the graph:
View Solution

