A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
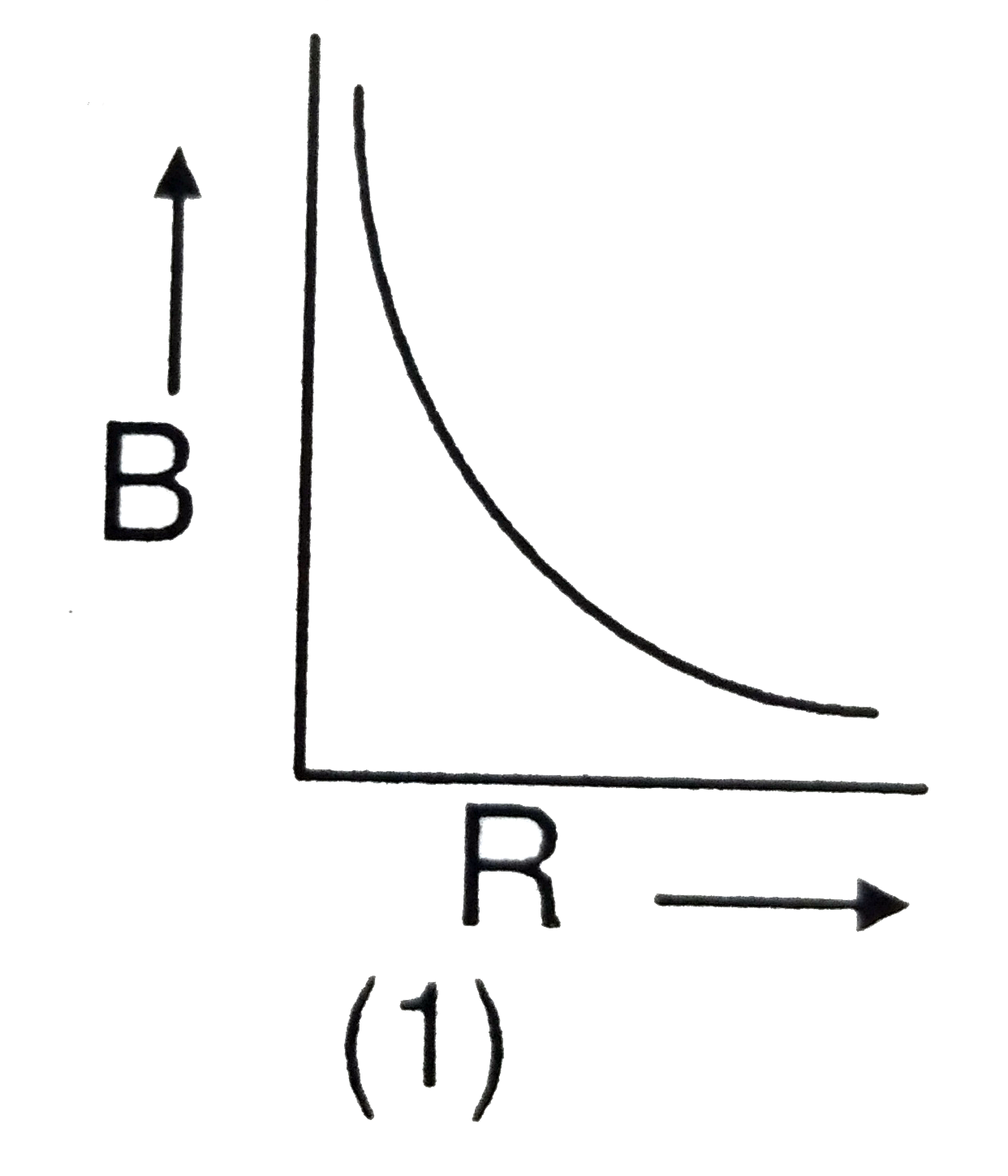

The correct Answer is:A
To solve the problem step by step, we will analyze the magnetic field at the center of a rotating non-conducting disc with a uniformly distributed charge Q over its surface.
Step 1: Understanding the Setup
We have a non-conducting disc of radius R with a total charge Q uniformly distributed over its surface. The disc rotates about an axis perpendicular to its plane and passing through its center with a constant angular velocity ω.
Step 2: Consider an Elemental Ring
To find the magnetic field at the center of the disc, we can consider an elemental ring of thickness dr at a distance r from the center of the disc. The area of this elemental ring is given by:
dA=2πrdr
Step 3: Charge on the Elemental Ring
The surface charge density σ is defined as:
σ=QπR2
The charge dQ on the elemental ring can be expressed as:
dQ=σdA=σ⋅2πrdr=QπR2⋅2πrdr=2QrR2dr
Step 4: Current Due to Rotation
The current I associated with the rotating ring can be calculated. The time period T for one complete rotation is given by:
T=2πω
Thus, the current I through the ring is:
I=dQT=dQ⋅ω2π=2QrR2⋅ω2πdr=QrωπR2dr
Step 5: Magnetic Field Contribution from the Elemental Ring
The magnetic field dB at the center of the disc due to the current I in the elemental ring is given by:
dB=μ0I2r
Substituting the expression for I:
dB=μ02r⋅QrωπR2dr=μ0Qω2πR2dr
Step 6: Total Magnetic Field at the Center
To find the total magnetic field B at the center of the disc, we integrate dB from r=0 to r=R:
B=∫R0dB=∫R0μ0Qω2πR2dr=μ0Qω2πR2⋅R=μ0Qω2πR
Step 7: Analyzing the Variation of Magnetic Field with Radius
From the expression we derived, we see that the magnetic field B is inversely proportional to the radius R:
B∝1R
This indicates that as the radius R increases, the magnetic field B at the center decreases.
Conclusion
The variation of the magnetic induction B at the center of the disc as the radius R changes, while keeping Q and ω constant, will be represented by a hyperbolic relationship, confirming that B decreases as R increases.
We have a non-conducting disc of radius R with a total charge Q uniformly distributed over its surface. The disc rotates about an axis perpendicular to its plane and passing through its center with a constant angular velocity ω.
To find the magnetic field at the center of the disc, we can consider an elemental ring of thickness dr at a distance r from the center of the disc. The area of this elemental ring is given by:
dA=2πrdr
The surface charge density σ is defined as:
σ=QπR2
The charge dQ on the elemental ring can be expressed as:
dQ=σdA=σ⋅2πrdr=QπR2⋅2πrdr=2QrR2dr
The current I associated with the rotating ring can be calculated. The time period T for one complete rotation is given by:
T=2πω
Thus, the current I through the ring is:
I=dQT=dQ⋅ω2π=2QrR2⋅ω2πdr=QrωπR2dr
The magnetic field dB at the center of the disc due to the current I in the elemental ring is given by:
dB=μ0I2r
Substituting the expression for I:
dB=μ02r⋅QrωπR2dr=μ0Qω2πR2dr
To find the total magnetic field B at the center of the disc, we integrate dB from r=0 to r=R:
B=∫R0dB=∫R0μ0Qω2πR2dr=μ0Qω2πR2⋅R=μ0Qω2πR
From the expression we derived, we see that the magnetic field B is inversely proportional to the radius R:
B∝1R
This indicates that as the radius R increases, the magnetic field B at the center decreases.
The variation of the magnetic induction B at the center of the disc as the radius R changes, while keeping Q and ω constant, will be represented by a hyperbolic relationship, confirming that B decreases as R increases.
Topper's Solved these Questions
Similar Questions
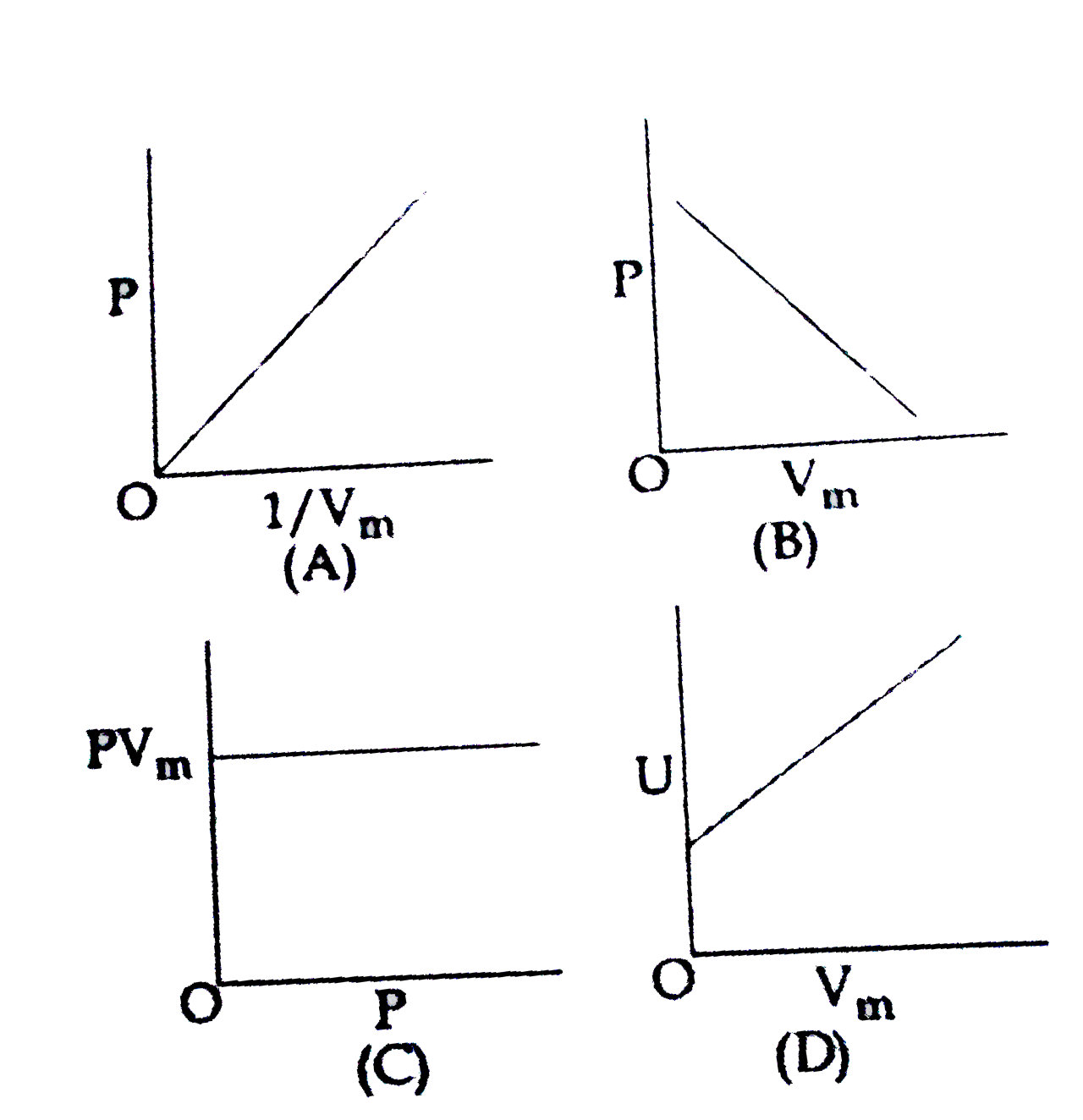
The combination of plots which does not represent isothermal expansion of an ideal gas is :
View SolutionA box weighs 196 N on a spring balance at the noth pole. Its weight recorded on the same balance if it is shifted to the equator is close to (take g=10ms−2 at the north pole and the radius of the earth = 6400 km) :
View SolutionIf x and y are arbitrary intensive variables, then
View SolutionA charge Q is uniformly distributed over the surface of non - conducting disc of radius R . The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionA circular disc is rotating in horizontal plane about vertical axis passing through its centre without friction with a person standing on the disc at its edge. If the person gently walks to centre of disc then its angular velocity
View SolutionA non conducting disc of radius R, charge q is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity ω charge q is uniformly distributed over its surface. The magnetic moment of the disc is
View SolutionA disc of mass m, radius r and carrying charge q, is rotating with angular speed omega about an axis passing through its centre and perpendicular to its plane. Calculate its magnetic moment
View SolutionA disc of radius 10 cm can rotate about an axis passing through its centre and perpendicular to its plane. A force of 10 N is applied along the tangent in the plane of the disc. If the moment of inertia of the disc about its centre is 5kgm2, then the increase in the angular velocity of the disc in 10 s will be
View SolutionRadius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
View SolutionRadius of gyration of a uniform circular disc about an axis passing through its centre of gravity and perpendicular to its plane is
View SolutionA plastic disc of radius 'R' has a charge 'q ' uniformly distributed over its surface. If the disc is rotated with a frequency 'f' about its axis, then the magnetic induction at the centre of the disc is given by
View SolutionA charge Q is uniformly distributed over the surface of nonconducting disc of the radius R. The disc rotates about an axis perpendicular to its planes and passing through its centre with an angular velocity ω. As a result of this rotation a magnetic field of induction B is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and varying the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure.
View SolutionA charge Q is uniformly distributed over the surface of nonconducting disc of the radius R. The disc rotates about an axis perpendicular to its planes and passing through its centre with an angular velocity 0. As a result of this rotation a magnetic field of induction B is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and varying the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure.
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R . It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
