A charge Q is uniformly distributed over the surface of nonconducting disc of the radius R. The disc rotates about an axis perpendicular to its planes and passing through its centre with an angular velocity ω. As a result of this rotation a magnetic field of induction B is obtained at the centre of the disc if we keep both the amount of charge placed on the disk and its angular velocity to be constant and varying the radius of the disc then the variation of the magnetic induction at the centre of the disc will be represented by the figure.

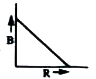


The correct Answer is:A
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBook:AAKASH SERIESChapter:MOVING CHARGES AND MAGNETISMExercise:EXERCISE-II
Explore 79 Videos
- MOTION IN A STRAIGHT LINE Book:AAKASH SERIESChapter:MOTION IN A STRAIGHT LINE Exercise:very Short answer type question
Explore 15 Videos
- NUCLEAR PHYSICSBook:AAKASH SERIESChapter:NUCLEAR PHYSICSExercise:ADDITIONAL PRACTICE PRACTICE SHEET (ADVANCED) Integer Type Questions
Explore 4 Videos
Similar Questions
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
View SolutionA charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View Solution
Knowledge Check
A charge Q is uniformly distributed over the surface of non - conducting disc of radius R. The disc rotates about an axis perpendicular to its plane and passing through its centre with an angular to its plane and passing through its centre of the disc. If we keep both the amount of charge placed on the disc and its angular velocity to be constant and vary the radius of the disc then the variation of the magnetic induction at the centre of the disc will br represented by the figure:
A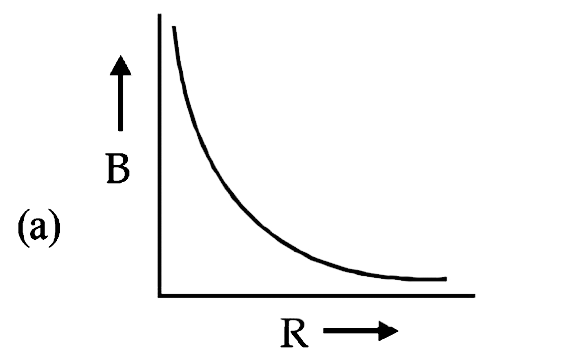 B
B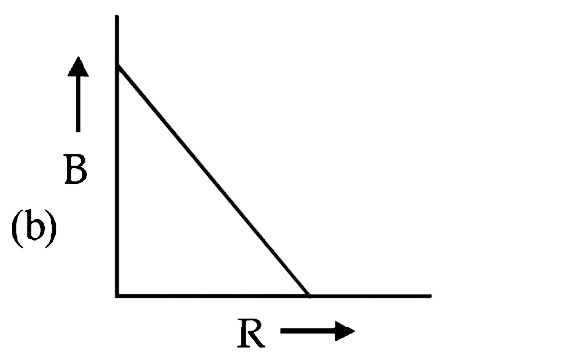 C
C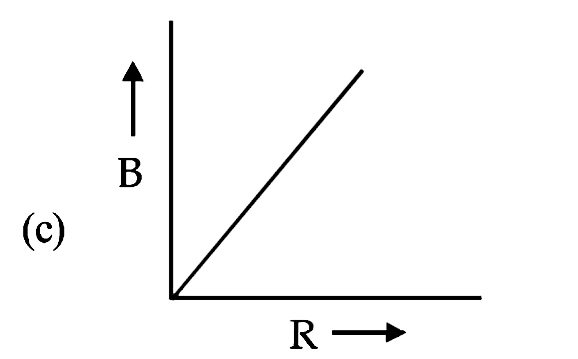 D
D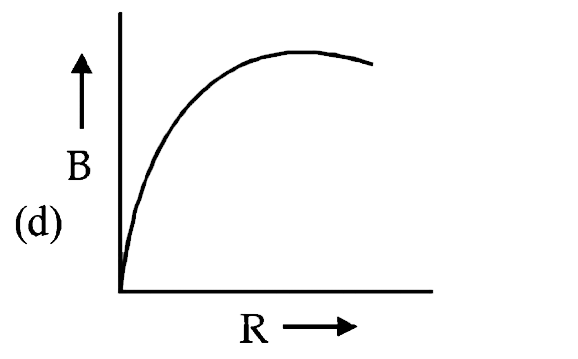
Radius of gyration of disc rotating about an axis perpendicular to its plane passing through through its centre is (If R is the radius of disc)
AR2BR√2CR√3DR3A non conducting disc of radius R, charge q is rotating about an axis passing through its centre and perpendicular to its plane with an angular velocity ω charge q is uniformly distributed over its surface. The magnetic moment of the disc is
A14qωR2B12qωRCqωRD12qωR2
A charge q is uniformly distributed on a non-conducting disc of radius R. It is rotated with an angular speed co about an axis passing through the centre of mass of the disc and perpendicular to its plane. Find the magnetic moment of the disc.
View SolutionCharge Q is uniformly distributed over a nonconducting ring of radius R and mass m. It is made to rotate about an axis passing through its centre and perpendicular to its plone with an angular velocity of rotation ω. Find its magnetic dipole moment and its ratio with angular momentum.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionA flat dielectric disc of radius R carries an exces charge on its surface. The surface charge density σ. The disc rotastes about an axis perpendicular to its lane passing thrugh the centre with angulasr velocity ω. Find the toruque on the disc if it is placed in a uniform magnetic field B directed perpendicular to the rotation axis.
View SolutionCharge q is uniformly distributed on a disc of radius r. If the disc is rotated with a frequency v, then magnetic field induction at the centre will be
View Solution
