A cylindrical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now
f
f2
3f4
2f
The correct Answer is:A
To solve the problem, we need to analyze the situation when the cylindrical tube is open at both ends and how the fundamental frequency changes when half of the tube is submerged in water.
1. Understand the Initial Condition:
- The cylindrical tube is open at both ends and has a fundamental frequency f in air.
- The length of the tube is L.
2. Determine the Wavelength in Air:
- For a tube open at both ends, the fundamental frequency corresponds to a wavelength λ such that:
λ2=L⟹λ=2L
- The speed of sound in air is denoted as v. Therefore, the fundamental frequency f can be expressed as:
f=vλ=v2L
3. Analyze the Condition When Half the Tube is in Water:
- When the tube is dipped in water, half of its length L2 is in water, and the other half L2 is in air.
- The portion of the tube in water behaves like a closed end (since water does not allow sound to propagate), while the portion in air remains open.
4. Determine the New Wavelength:
- For a tube that is closed at one end and open at the other, the fundamental frequency corresponds to a wavelength λ′ such that:
λ′4=L2⟹λ′=2L
5. Calculate the New Frequency:
- The speed of sound in air remains v, and the new frequency f′ can be calculated as:
f′=vλ′=v2L
- Notice that this is the same expression as for the original frequency f.
6. Conclusion:
- Therefore, the fundamental frequency of the air column when half of the tube is submerged in water remains the same:
f′=f
Final Answer:
The fundamental frequency of the air column when half of the tube is submerged in water is f.
- The cylindrical tube is open at both ends and has a fundamental frequency f in air.
- The length of the tube is L.
- For a tube open at both ends, the fundamental frequency corresponds to a wavelength λ such that:
λ2=L⟹λ=2L
- The speed of sound in air is denoted as v. Therefore, the fundamental frequency f can be expressed as:
f=vλ=v2L
- When the tube is dipped in water, half of its length L2 is in water, and the other half L2 is in air.
- The portion of the tube in water behaves like a closed end (since water does not allow sound to propagate), while the portion in air remains open.
- For a tube that is closed at one end and open at the other, the fundamental frequency corresponds to a wavelength λ′ such that:
λ′4=L2⟹λ′=2L
- The speed of sound in air remains v, and the new frequency f′ can be calculated as:
f′=vλ′=v2L
- Notice that this is the same expression as for the original frequency f.
- Therefore, the fundamental frequency of the air column when half of the tube is submerged in water remains the same:
f′=f
The fundamental frequency of the air column when half of the tube is submerged in water is f.
Topper's Solved these Questions
Similar Questions
A cylindrical tube, open at both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of its length is in water. The fundamental frequency of the air column is now
(a) f/2
(b) 3f/4
(C ) f
(d) 2f
View SolutionA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
View Solution
Knowledge Check
In an organ pipe of length L open at both ends, the fundamental mode has a frequency
(where v is a speed of sound in air)Av2L and only odd harmonies are present.Bv2L and only even harmonies are present.Cv2L and all harmonies are present.Dv4L and only odd harmonies are present.
A cylinderical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View SolutionA pipe open at both ends has a fundamental frequency f in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now :
View SolutionA pipe open at both ends has a fundamental frequency f in air. The pipe is dippoed vertically in water so that half of it is in water. The fundamental frequency of the air column is now :-
View SolutionA cylindrical tube open at both the ends has a
fundamental frequency of 390 Hz in air. If 14 th of the tube is immesed vertically in water the fundamental
frequency of air column is
View SolutionA cylindrical tube, is open at both the ends, it has fundamental frequency 200 Hz in air. Now half of length contains water. The fundamental frequency will now be
View Solution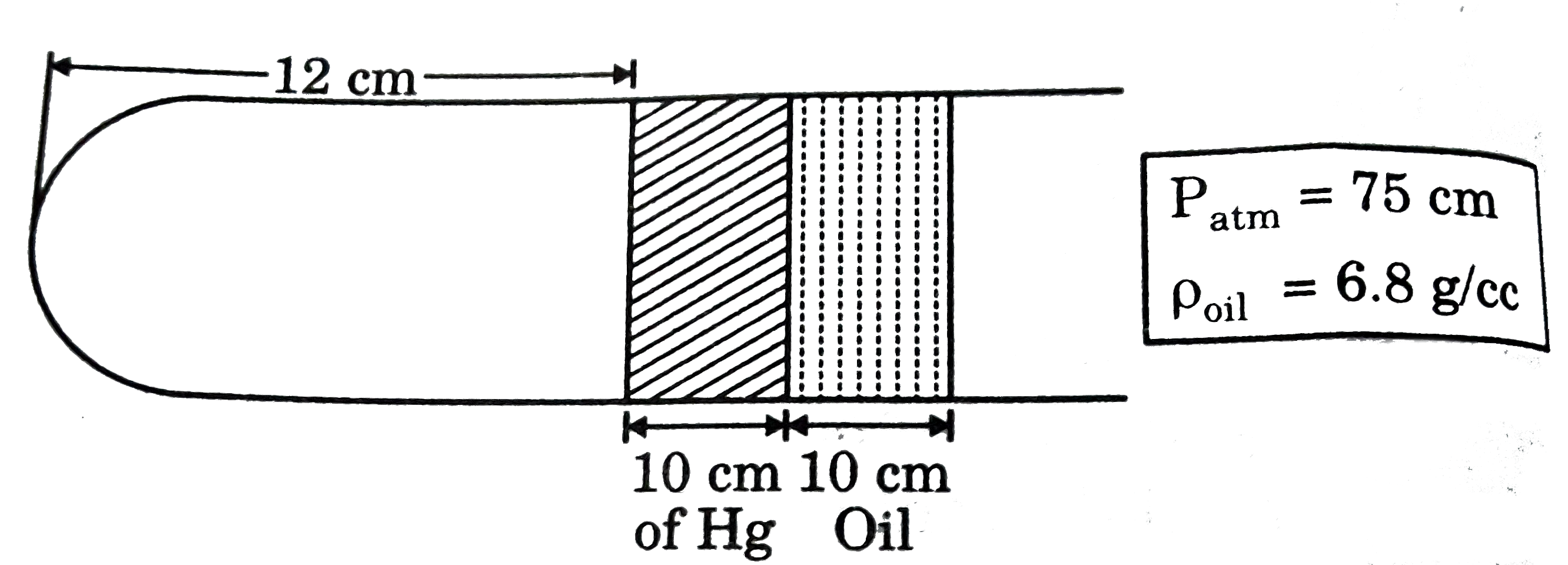
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionThe length of an organ pipe open at both ends is 0.5 m. Calculate the fundamental frequency of the pipe, if the velocity of sound in air be 350 m/s. If one end of the pipe is closed then what will be the fundamental frequency ?
View Solution
