A cylindrical tube open at both the ends has a
fundamental frequency of 390 Hz in air. If 14 th of the tube is immesed vertically in water the fundamental
frequency of air column is
(a)260 Hz
(b)130 Hz
(c)390 Hz
(d)520 Hz
The correct Answer is:A
To solve the problem step by step, we will follow the principles of sound waves in tubes and the relationship between frequency, wavelength, and length of the tube.
1. Understanding the Problem:
- We have a cylindrical tube that is open at both ends.
- The fundamental frequency of the tube in air is given as f=390Hz.
- When 14 of the tube is immersed in water, we need to find the new fundamental frequency of the air column.
2. Determine the Length of the Tube:
- The fundamental frequency of a tube open at both ends is given by the formula:
f=v2L
where v is the speed of sound in air and L is the length of the tube.
- Rearranging the formula gives:
L=v2f
3. Calculate the Length of the Tube:
- We need the speed of sound in air, which is approximately v=343m/s (at room temperature).
- Substituting the values into the length formula:
L=343m/s2×390Hz=343780≈0.440m
4. Determine the New Length of the Air Column:
- When 14 of the tube is immersed in water, the length of the air column becomes:
L′=L−14L=34L
- Therefore:
L′=34×0.440m=0.330m
5. Calculate the New Fundamental Frequency:
- The new fundamental frequency f′ for the air column is given by:
f′=v2L′
- Substituting L′:
f′=343m/s2×0.330m=3430.660≈519.7Hz
6. Final Calculation:
- Rounding off, the new fundamental frequency is approximately:
f′≈520Hz
Conclusion:
The fundamental frequency of the air column when 14 of the tube is immersed in water is approximately 520 Hz.
- We have a cylindrical tube that is open at both ends.
- The fundamental frequency of the tube in air is given as f=390Hz.
- When 14 of the tube is immersed in water, we need to find the new fundamental frequency of the air column.
- The fundamental frequency of a tube open at both ends is given by the formula:
f=v2L
where v is the speed of sound in air and L is the length of the tube.
- Rearranging the formula gives:
L=v2f
- We need the speed of sound in air, which is approximately v=343m/s (at room temperature).
- Substituting the values into the length formula:
L=343m/s2×390Hz=343780≈0.440m
- When 14 of the tube is immersed in water, the length of the air column becomes:
L′=L−14L=34L
- Therefore:
L′=34×0.440m=0.330m
- The new fundamental frequency f′ for the air column is given by:
f′=v2L′
- Substituting L′:
f′=343m/s2×0.330m=3430.660≈519.7Hz
- Rounding off, the new fundamental frequency is approximately:
f′≈520Hz
The fundamental frequency of the air column when 14 of the tube is immersed in water is approximately 520 Hz.
Similar Questions
A cylinderical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of air column is now
View SolutionA cylindrical tube, open at the both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of it is in water . The fundamental frequency of the air column is now-
View SolutionA pipe open at both ends has a fundamental frequency f in air. The pipe is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now :
View SolutionA cylindrical tube, open at both ends, has a fundamental frequency f in air . The tube is dipped vertically in water so that half of its length is in water. The fundamental frequency of the air column is now
(a) f/2
(b) 3f/4
(C ) f
(d) 2f
View SolutionA cylindrical tube, is open at both the ends, it has fundamental frequency 200 Hz in air. Now half of length contains water. The fundamental frequency will now be
View SolutionA pipe open at both ends has a fundamental frequency f in air. The pipe is dippoed vertically in water so that half of it is in water. The fundamental frequency of the air column is now :-
View SolutionA cylindrical tube open at both ends, has a fundamental frequency f in air. The tube is dipped vertically in air. The tube is dipped vertically in water so that half of it is in water. The fundamental frequency of the air column is now
View SolutionThe fundamental frequency of an open organ pipe is n. If one of its ends is closed then its fundamental frequency will be –
View Solution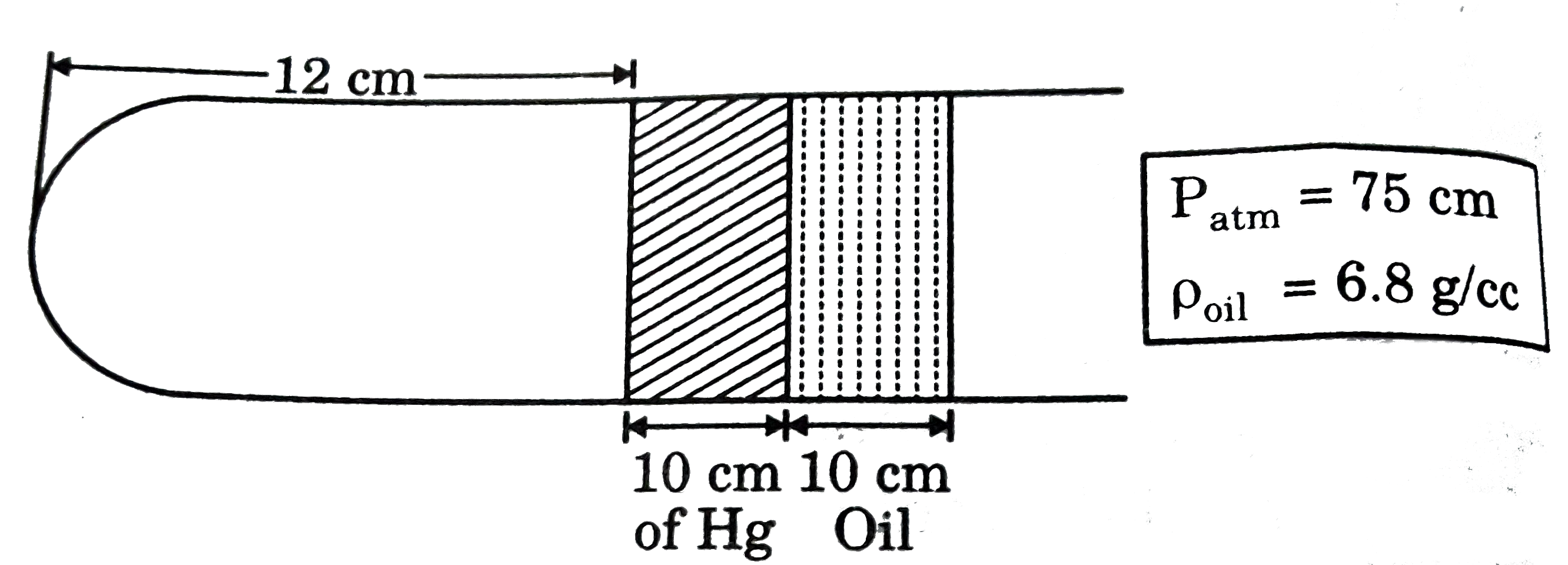
If above tube is placed vertically with the open and upward then find the length of the air column.
View SolutionThe string of a violin has a fundamental frequency of 440 Hz. If the violin string is shortend by one fifth, itd fundamental frequency will be changed to
View Solution
