The supply voltage to room is 120 V. The resistance of the lead wires is 6Ω. A 60 W bulb is already switched on. What is the decrease of voltage across the bulb, when a 240 W heater is switched on in parallel to the bulb?
2.9 Volt
13.3 Volt
10.04 Volt
zero volt
The correct Answer is:C
To solve the problem, we will follow these steps:
Step 1: Calculate the resistance of the 60 W bulb
The power (P) of the bulb is given as 60 W and the supply voltage (V) is 120 V. We can use the formula for power:
P=V2R
Rearranging this gives:
R=V2P
Substituting the values:
Rbulb=120260=1440060=240Ω
Step 2: Calculate the resistance of the 240 W heater
Using the same formula for the heater:
P=240W
Rheater=1202240=14400240=60Ω
Step 3: Calculate the voltage drop across the bulb when only the bulb is on
When only the bulb is on, the total resistance in the circuit is the sum of the bulb's resistance and the lead wire's resistance:
Rtotal=Rbulb+Rwire=240+6=246Ω
The voltage drop across the bulb can be calculated using the voltage divider rule:
Vbulb=V×RbulbRtotal=120×240246
Calculating this gives:
Vbulb=120×240246≈117.07V
Step 4: Calculate the equivalent resistance when both the bulb and heater are on
When the bulb and heater are on, they are in parallel. The equivalent resistance Req of the bulb and heater can be calculated as:
1Req=1Rbulb+1Rheater
Substituting the values:
1Req=1240+160
Finding a common denominator (240):
1Req=1240+4240=5240
Thus,
Req=2405=48Ω
Step 5: Calculate the new voltage drop across the bulb with both devices on
Now, the total resistance in the circuit is:
Rtotal=Req+Rwire=48+6=54Ω
Using the voltage divider rule again:
V′bulb=V×ReqRtotal=120×4854
Calculating this gives:
V′bulb=120×4854≈106.67V
Step 6: Calculate the decrease in voltage across the bulb
The decrease in voltage across the bulb when the heater is switched on is:
ΔV=Vbulb−V′bulb=117.07−106.67≈10.4V
Final Answer
The decrease in voltage across the bulb when the heater is switched on is approximately 10.4 V.
---
The power (P) of the bulb is given as 60 W and the supply voltage (V) is 120 V. We can use the formula for power:
P=V2R
Rearranging this gives:
R=V2P
Substituting the values:
Rbulb=120260=1440060=240Ω
Using the same formula for the heater:
P=240W
Rheater=1202240=14400240=60Ω
When only the bulb is on, the total resistance in the circuit is the sum of the bulb's resistance and the lead wire's resistance:
Rtotal=Rbulb+Rwire=240+6=246Ω
The voltage drop across the bulb can be calculated using the voltage divider rule:
Vbulb=V×RbulbRtotal=120×240246
Calculating this gives:
Vbulb=120×240246≈117.07V
When the bulb and heater are on, they are in parallel. The equivalent resistance Req of the bulb and heater can be calculated as:
1Req=1Rbulb+1Rheater
Substituting the values:
1Req=1240+160
Finding a common denominator (240):
1Req=1240+4240=5240
Thus,
Req=2405=48Ω
Now, the total resistance in the circuit is:
Rtotal=Req+Rwire=48+6=54Ω
Using the voltage divider rule again:
V′bulb=V×ReqRtotal=120×4854
Calculating this gives:
V′bulb=120×4854≈106.67V
The decrease in voltage across the bulb when the heater is switched on is:
ΔV=Vbulb−V′bulb=117.07−106.67≈10.4V
The decrease in voltage across the bulb when the heater is switched on is approximately 10.4 V.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If R1andR2 are filament resistances of a 200 W and a 100 W bulb respectively, designed to operate on the same voltage, then :
AR1=R2BR2=2R1CR2=4R1DR1=4R2A light bulb is rated at 100 W for a 220 V ac supply . The resistance of the bulb is
A284ΩB384ΩC484ΩD584Ω
When two electric bulbs of 40W and 60W are connected in parallel, then the:
View SolutionAll bulbs consume same power. The resistance of bulb 1 is 36Ω . Answer the following questions:
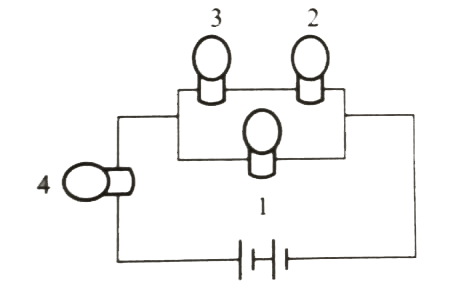
What is the voltage output of the battery if the power of each bulb is 4W?
View SolutionAn electric bulb is rated "220 V, 100 W'.
What is its resistance ?
View SolutionIf a wire of resistance 20Ω is covered with ice and a voltage of 210V is applied across the wire , then the rate of melting of ice is
View SolutionA 120V house circuit has the following light bulbs switched on : 40W,60W and 75W. Find the equivalent resistance of these bulbs.
View SolutionA 50 W bulb is in series with a room heater and the combination is conneted across the mains. To get max, heater output, the 50 W bulb should be replaced by :
View Solution
