A sonometer wire of length 1.5m is made of steel. The tension in it produces an elastic strain of 1%. What is the fundamental frequency of steel if density and elasticity of steel are 7.7×103kg/m3 and 2.2×1011N/m2 respectively ?
178.2 Hz
200.5 Hz
770 Hz
188.5 Hz
The correct Answer is:A
To find the fundamental frequency of the sonometer wire made of steel, we will follow these steps:
Step 1: Understand the Formula
The fundamental frequency f of a vibrating string (or wire) is given by the formula:
f=12L√Tμ
where:
- L is the length of the wire,
- T is the tension in the wire,
- μ is the linear mass density of the wire.
Step 2: Calculate the Linear Mass Density μ
The linear mass density μ can be expressed in terms of the density ρ and the cross-sectional area A of the wire:
μ=mL=ρ⋅A
However, we do not have the area A directly, but we can use the relationship of tension and stress.
Step 3: Calculate the Tension T
The tension T in the wire can be related to the stress and strain. The stress σ is given by:
σ=TA
And stress is also defined as:
σ=E⋅strain
where E is the Young's modulus of the material, and the strain is given as 1%=0.01.
Thus, we can write:
TA=E⋅strain
From this, we can express T:
T=E⋅strain⋅A
Substituting the values:
- E=2.2×1011N/m2
- Strain = 0.01
This gives:
T=2.2×1011⋅0.01⋅A=2.2×109⋅A
Step 4: Substitute T and μ into the Frequency Formula
Now substituting T and μ into the frequency formula:
f=12L√Tμ=12L√2.2×109⋅Aρ⋅A
The area A cancels out:
f=12L√2.2×109ρ
Step 5: Substitute Known Values
Now substituting the known values:
- L=1.5m
- ρ=7.7×103kg/m3
Thus:
f=12⋅1.5√2.2×1097.7×103
Step 6: Calculate the Frequency
Calculating the values:
1. Calculate 2.2×1097.7×103:
2.2×1097.7×103≈285714.29
2. Now take the square root:
√285714.29≈534.52
3. Finally calculate f:
f=13⋅534.52≈178.17Hz
Final Answer
Thus, the fundamental frequency of the steel sonometer wire is approximately:
178.2Hz
The fundamental frequency f of a vibrating string (or wire) is given by the formula:
f=12L√Tμ
where:
- L is the length of the wire,
- T is the tension in the wire,
- μ is the linear mass density of the wire.
The linear mass density μ can be expressed in terms of the density ρ and the cross-sectional area A of the wire:
μ=mL=ρ⋅A
However, we do not have the area A directly, but we can use the relationship of tension and stress.
The tension T in the wire can be related to the stress and strain. The stress σ is given by:
σ=TA
And stress is also defined as:
σ=E⋅strain
where E is the Young's modulus of the material, and the strain is given as 1%=0.01.
TA=E⋅strain
From this, we can express T:
T=E⋅strain⋅A
Substituting the values:
- E=2.2×1011N/m2
- Strain = 0.01
T=2.2×1011⋅0.01⋅A=2.2×109⋅A
Now substituting T and μ into the frequency formula:
f=12L√Tμ=12L√2.2×109⋅Aρ⋅A
The area A cancels out:
f=12L√2.2×109ρ
Now substituting the known values:
- L=1.5m
- ρ=7.7×103kg/m3
f=12⋅1.5√2.2×1097.7×103
Calculating the values:
1. Calculate 2.2×1097.7×103:
2.2×1097.7×103≈285714.29
2. Now take the square root:
√285714.29≈534.52
3. Finally calculate f:
f=13⋅534.52≈178.17Hz
Thus, the fundamental frequency of the steel sonometer wire is approximately:
178.2Hz
Topper's Solved these Questions
Similar Questions
A wire of radius 10−3m and length 2m is stretched by a force of 50 N. Calculate the fundamental frequency of the note emitted by it. Density of wire is 1.6.×103 kg m−3.
View SolutionIn an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is, [Given, the Young’s Modulus for steel and brass are, respectively, 120×109N/m2and60×109N/m2
View SolutionIn an experiment, brass and steel wires of length 1 m each with areas of cross section 1mm2 are used. The wires are connected in series and one end of the combined wire is connected to a rigid support and other end is subjected to elongation. The stress required to produce a net elongation of 0.2 mm is, [Given, the Young’s Modulus for steel and brass are, respectively, 120×109N/m2and60×109N/m2
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionCalculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
View SolutionA block of weight 100 N is suspended by copper and steel wires of same cross sectional area 0.5cm2 and, length √3 m and 1m, respectively. Their other ends are fixed on a ceiling as shown in figure. The angles subtended by copper and steel wires with ceiling are 30∘and60∘, respectively. If elongation in copper wire is (ΔlC) and elongation in steel wire is (Δls), then the ratio ΔlCΔls is -
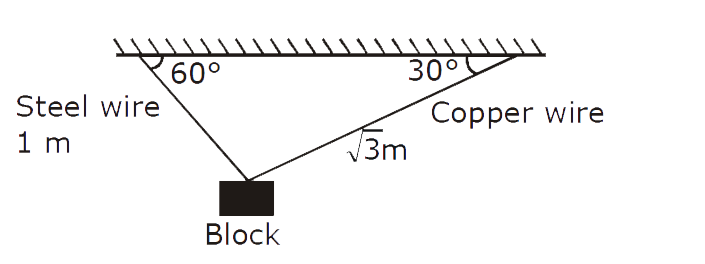
[Young's modulus for copper and steel are 1×1011N/m2and2×1011N/m2, respectively]
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionTwo metal spheres are falling through a liquid of density 2×103kg/m3 with the same uniform speed. The material density of sphere 1 and sphere 2 are 8×103kg/m3 and 11×103kg/m3 respectively. The ratio of their radii is :-
View SolutionA rigid bar of mass 15 kg is supported symmetrically by three wires, each of length 2 m. The wires at the endpoints are made of copper and the middle one is made of steel. If the tension in each wire is the same, then the diameter of copper wire to the diameter of steel wire is [Given, Ycopper=1.1×1011N m−1andYsteel=1.9×1011N m−2]
View SolutionWhat is the radius of a steel sphere that wil float on water with exactly half the sphere submerged ? Density of steel is 7.9×103kg/m3 and surface tension of water is 7×10−2N.
View Solution
