Calculate the speed of longitudinal wave in steel. Young's modulus for steel is 3×1010N/m2 and its density 1.2×103kg/m3
To calculate the speed of a longitudinal wave in steel, we can use the formula:
V=√Yρ
where:
- V is the speed of the wave,
- Y is Young's modulus,
- ρ is the density of the material.
1. Identify the given values:
- Young's modulus for steel, Y=3×1010N/m2
- Density of steel, ρ=1.2×103kg/m3
2. Substitute the values into the formula:
V=√3×10101.2×103
3. Simplify the fraction inside the square root:
V=√31.2×1010103
V=√2.5×107
4. Calculate the square root:
- First, find the square root of 2.5:
√2.5≈1.58
- Then, find the square root of 107:
√107=103.5=103×√10≈1000×3.16≈3162.3
5. Combine the results:
V≈1.58×3162.3≈5000m/s
6. Final result:
V≈5000m/s
Final Answer:
The speed of the longitudinal wave in steel is approximately 5000m/s.
- V is the speed of the wave,
- Y is Young's modulus,
- ρ is the density of the material.
- Young's modulus for steel, Y=3×1010N/m2
- Density of steel, ρ=1.2×103kg/m3
V=√3×10101.2×103
V=√31.2×1010103
V=√2.5×107
- First, find the square root of 2.5:
√2.5≈1.58
- Then, find the square root of 107:
√107=103.5=103×√10≈1000×3.16≈3162.3
V≈1.58×3162.3≈5000m/s
V≈5000m/s
The speed of the longitudinal wave in steel is approximately 5000m/s.
Topper's Solved these Questions
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:Try Yourself
Explore 65 Videos
- WAVESBook:AAKASH INSTITUTE ENGLISHChapter:WAVESExercise:Assignment (Section-A)
Explore 55 Videos
- WAVE OPTICSBook:AAKASH INSTITUTE ENGLISHChapter:WAVE OPTICSExercise:Assignment (Section-J (Aakash Challengers question))
Explore 1 Video
- WORK, ENERGY AND POWERBook:AAKASH INSTITUTE ENGLISHChapter:WORK, ENERGY AND POWERExercise:Assignment (SECTION - D)
Explore 13 Videos
Similar Questions
Calculate the speed of longitudinal sound wave in a liquid. The bulk modulus for the liquid is 20×109N/m2 and its density is 9.5×103kg/m3.
View SolutionYoung 's modulus of steel is 2.0×1011Nm/(2). Express it is dynecm2.
View SolutionThe speed of longitudinal mechanical wave in a material is 4300 m/s. young's modulus of the material is 15×109N/m2. What is the density of the material?
View SolutionA steel rod 2.5m long is rigidly clamped at its centre C and longitudinal waves are set up on both sides of C by rubbing along the rod . Young's modulus for steel =2×1011N/m2 , density of steel =8000kg/m3

If the clamp of the rod be shifted to its end A and totally four antinodes are observed in the rod when longitudinal waves are set up in it , the frequency of vibration of the rod in this mode is
View SolutionCalculate the Poisson's ratio for steel. Given that Young's modulus is 2×1011Nm−2 and rigidity modulus is 8×1010Nm−2.
View SolutionA light rod AC of length 2.00 m is suspended from the ceiling horizontally by means of two vertical wires of equal length tied to its ends. One of the wires is made of steel and is of cross-section 10−3m2 and the other is of brass of cross-section 2×10−3m2. The position of point D from end A along the rod at which a weight may be hung to produce equal stress in both the wires is [Young's modulus of steel is 2×1011Nm2 and for brass is 1×1011Nm−2]
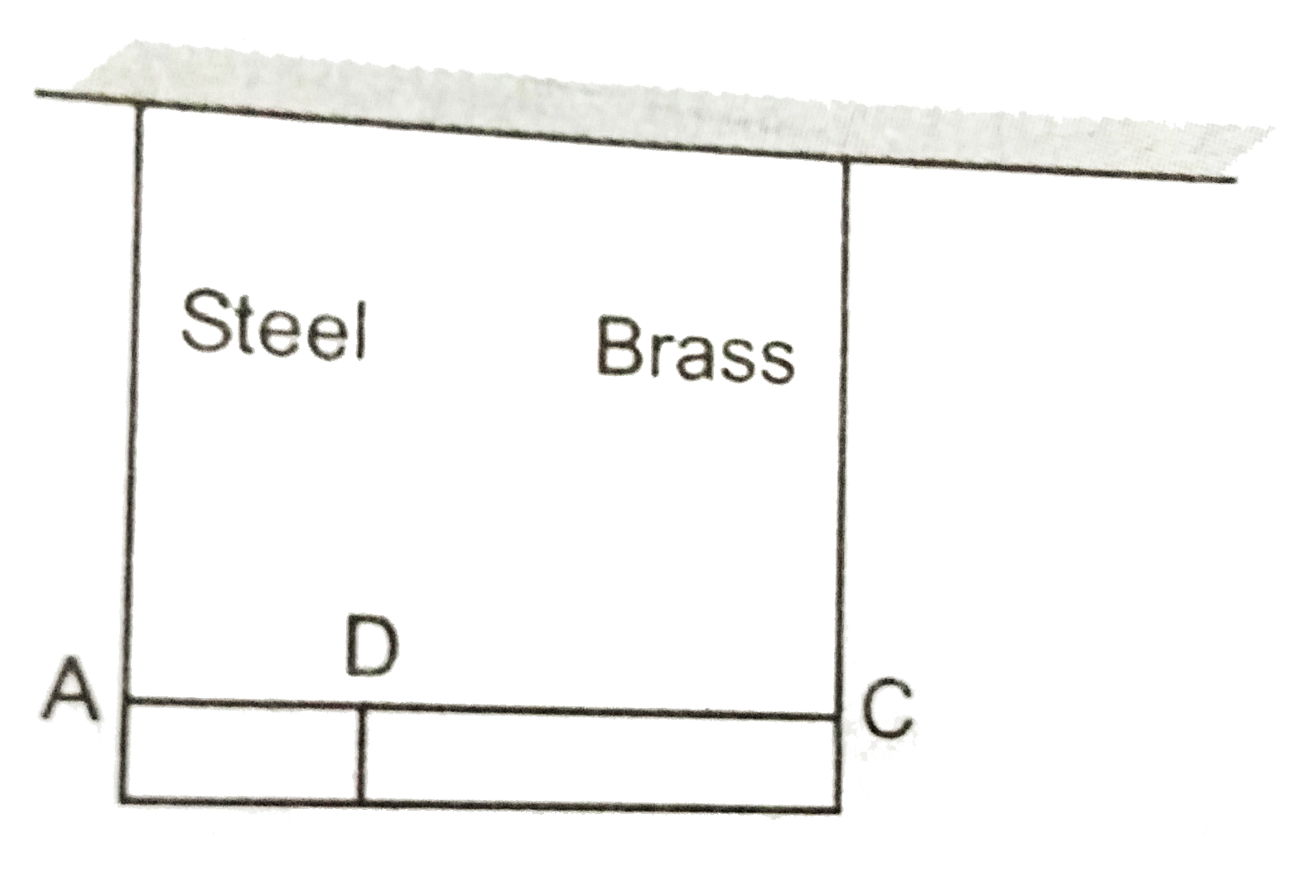
View Solution(a) A wire 4m long and 0.3 mm, calculate the potential energy stored in the wire.
Young's modulus for the material of wire is 2.0×1011N/m2.
View SolutionLongitudinal waves are produced in four identical rods in different situations. Their mode of vibration are fixed points (with bold point) are shown in the column-2 , their frequencies are given in the column -1 and their wavelength in column-3 . Each of the rod has length 1 m young's modulus of elasticity 2×1012N/m2 and density 5×103kg/m3
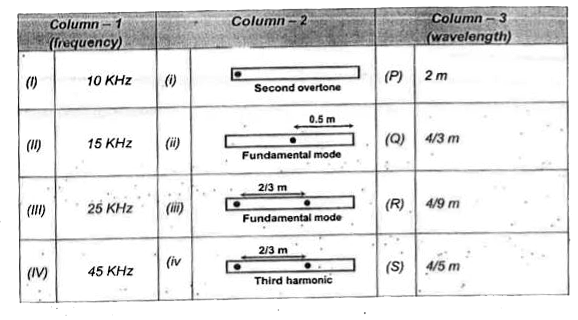
Pick the correct combination.
View SolutionLongitudinal waves are produced in four identical rods in different situations. Their mode of vibration are fixed points (with bold point) are shown in the column-2 , their frequencies are given in the column -1 and their wavelength in column-3 . Each of the rod has length 1 m young's modulus of elasticity 2×1012N/m2 and density 5×103kg/m3
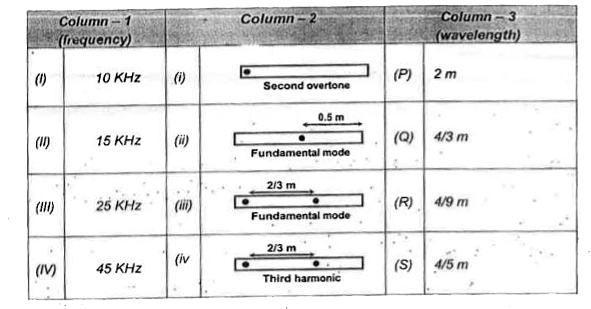
Pick the correct combination for the fundamental mode.
View SolutionLongitudinal waves are produced in four identical rods in different situations. Their mode of vibration are fixed points (with bold point) are shown in the column-2 , their frequencies are given in the column -1 and their wavelength in column-3 . Each of the rod has length 1 m young's modulus of elasticity 2×1012N/m2 and density 5×103kg/m3

Pick the correct combination for the least wavelength.
View Solution