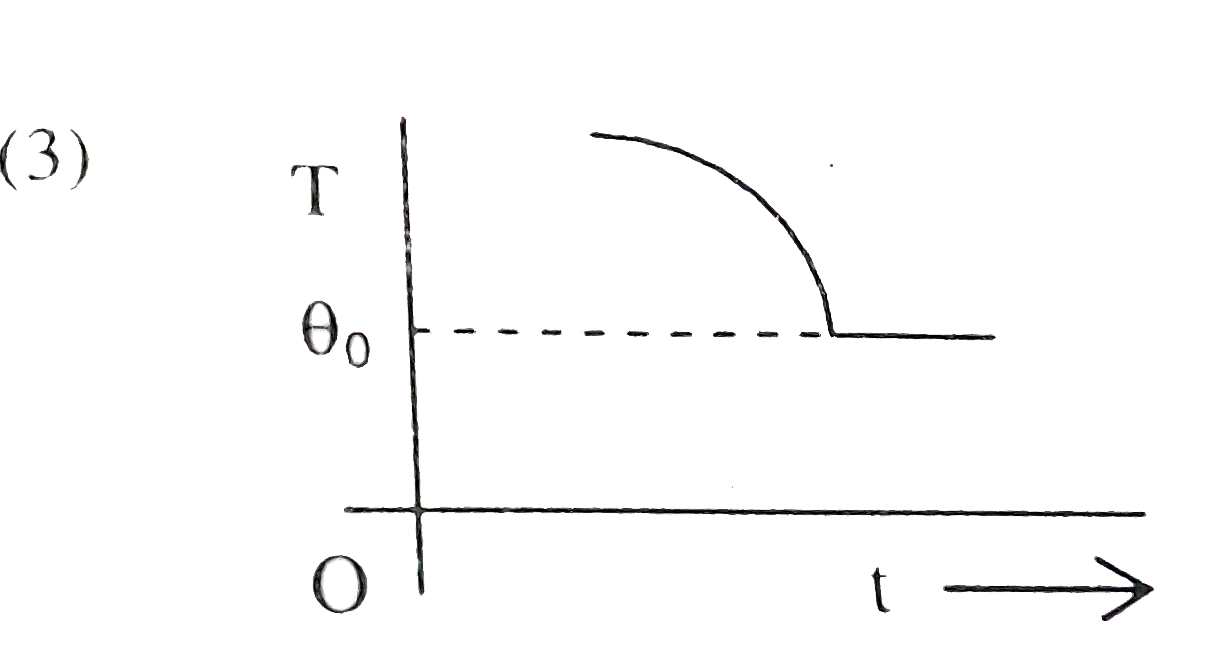
If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to


The correct Answer is:B
To solve the problem of how the temperature T of a piece of metal changes over time t as it cools in a room at temperature θ0, we can apply Newton's Law of Cooling. Here is a step-by-step solution:
Step 1: Understand Newton's Law of Cooling
According to Newton's Law of Cooling, the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
dTdt=−k(T−θ0)
where:
- T is the temperature of the metal,
- θ0 is the ambient temperature,
- k is a positive constant.
Step 2: Rearranging the Equation
We can rearrange the equation to isolate the variables:
dTT−θ0=−kdt
Step 3: Integrate Both Sides
Next, we integrate both sides. The left side will be integrated with respect to T and the right side with respect to t:
∫dTT−θ0=−k∫dt
This gives us:
ln|T−θ0|=−kt+C
where C is the constant of integration.
Step 4: Solve for T
To solve for T, we exponentiate both sides:
|T−θ0|=e−kt+C=eCe−kt
Let A=eC, then we can write:
T−θ0=Ae−kt
Thus, we have:
T=θ0+Ae−kt
Step 5: Determine the Constant A
At t=0, the initial temperature T(0)=θ:
θ=θ0+A
This implies:
A=θ−θ0
Substituting A back into the equation gives:
T=θ0+(θ−θ0)e−kt
Step 6: Analyze the Behavior of the Function
As t approaches infinity, the term e−kt approaches 0, leading to:
T→θ0
At t=0, T=θ. The graph of T versus t will show an exponential decay towards θ0.
Conclusion
The graph of the temperature T of the metal versus time t will be an exponential decay curve approaching the ambient temperature θ0.
According to Newton's Law of Cooling, the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
dTdt=−k(T−θ0)
where:
- T is the temperature of the metal,
- θ0 is the ambient temperature,
- k is a positive constant.
We can rearrange the equation to isolate the variables:
dTT−θ0=−kdt
Next, we integrate both sides. The left side will be integrated with respect to T and the right side with respect to t:
∫dTT−θ0=−k∫dt
This gives us:
ln|T−θ0|=−kt+C
where C is the constant of integration.
To solve for T, we exponentiate both sides:
|T−θ0|=e−kt+C=eCe−kt
Let A=eC, then we can write:
T−θ0=Ae−kt
Thus, we have:
T=θ0+Ae−kt
At t=0, the initial temperature T(0)=θ:
θ=θ0+A
This implies:
A=θ−θ0
Substituting A back into the equation gives:
T=θ0+(θ−θ0)e−kt
As t approaches infinity, the term e−kt approaches 0, leading to:
T→θ0
At t=0, T=θ. The graph of T versus t will show an exponential decay towards θ0.
The graph of the temperature T of the metal versus time t will be an exponential decay curve approaching the ambient temperature θ0.
Topper's Solved these Questions
Similar Questions
Knowledge Check
This metal is a liquid at room temperature :
APotassiumBZincCGoldDMercury
The graph between the (velocity2) and temperature T of a gas is
View SolutionThis non-metal is liquid at room temperature :
View SolutionName the following:
A metal which is liquid at room temperature,
View SolutionA piece of glass is heated to a high temperature and then allowed to cool. If it cracks, a probable reason for this is the following property of glass
View SolutionName a metal which is liquid at room temperature.
View SolutionA very thin metallic shell of radius r is heated to temperature T and then allowed to cool. The rate of cooling of shell is proportional to
View SolutionA body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
View Solution
