A body with an initial temperature θ1 is allowed to cool in a surrounding which is at a constant temperature of θ0(θ<θ1) Assume that Newton's law of cooling is obeyed Let k= constant The temperature of the body after time t is best experssed by .
(a)(θi−θ0)e−kt
(b)(θi−θ0)1n(kt)
(c)θ0+(θi−θ0)e−kt
(d)θie−kt−θ0
The correct Answer is:C
To solve the problem using Newton's law of cooling, we follow these steps:
Step 1: Understand Newton's Law of Cooling
Newton's law of cooling states that the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where:
- θ is the temperature of the body at time t,
- θ0 is the constant surrounding temperature,
- k is a positive constant.
Step 2: Rearranging the Equation
We can rearrange the equation to separate variables:
dθθ−θ0=−kdt
Step 3: Integrate Both Sides
Next, we integrate both sides. The left side will be integrated with respect to θ and the right side with respect to t:
∫dθθ−θ0=−k∫dt
This gives us:
ln|θ−θ0|=−kt+C
where C is the constant of integration.
Step 4: Solve for the Constant of Integration
To find C, we use the initial condition. At t=0, the temperature of the body is θ1:
ln|θ1−θ0|=C
Thus, we can rewrite the equation as:
ln|θ−θ0|=−kt+ln|θ1−θ0|
Step 5: Exponentiate to Solve for θ
Exponentiating both sides gives us:
|θ−θ0|=|θ1−θ0|e−kt
Step 6: Remove Absolute Values
Since θ<θ1 and θ0<θ1, we can drop the absolute values:
θ−θ0=(θ1−θ0)e−kt
Step 7: Rearranging to Find θ
Finally, we rearrange to express θ:
θ=θ0+(θ1−θ0)e−kt
This is the expression for the temperature of the body after time t.
Final Answer
The temperature of the body after time t is given by:
θ(t)=θ0+(θ1−θ0)e−kt
Newton's law of cooling states that the rate of change of temperature of an object is proportional to the difference between its temperature and the ambient temperature. Mathematically, this can be expressed as:
dθdt=−k(θ−θ0)
where:
- θ is the temperature of the body at time t,
- θ0 is the constant surrounding temperature,
- k is a positive constant.
We can rearrange the equation to separate variables:
dθθ−θ0=−kdt
Next, we integrate both sides. The left side will be integrated with respect to θ and the right side with respect to t:
∫dθθ−θ0=−k∫dt
This gives us:
ln|θ−θ0|=−kt+C
where C is the constant of integration.
To find C, we use the initial condition. At t=0, the temperature of the body is θ1:
ln|θ1−θ0|=C
Thus, we can rewrite the equation as:
ln|θ−θ0|=−kt+ln|θ1−θ0|
Exponentiating both sides gives us:
|θ−θ0|=|θ1−θ0|e−kt
Since θ<θ1 and θ0<θ1, we can drop the absolute values:
θ−θ0=(θ1−θ0)e−kt
Finally, we rearrange to express θ:
θ=θ0+(θ1−θ0)e−kt
The temperature of the body after time t is given by:
θ(t)=θ0+(θ1−θ0)e−kt
Topper's Solved these Questions
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Main (Archive) Level - 148videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - JEE Advanced(Archive) Level - 21videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - PROPERTIES OF MATTEREXERCISE - Level -190videos
PROPERTIES OF MATTER
- BOOK - VMC MODULES ENGLISHCHAPTER - MOVING CHARGES & MAGNETISM EXERCISE - IN-CHAPTER EXERCISE-K10videos
MOVING CHARGES & MAGNETISM
- BOOK - VMC MODULES ENGLISHCHAPTER - QUIZEXERCISE - PHYSICS30videos
QUIZ
Similar Questions
If a piece of metal is heated to temperature θ and the allowed to cool in a room which is at temperature θ0, the graph between the temperature T of the metal and time t will be closet to
View SolutionA body cools from a temperature 3T to 2T in 10 minutes. The room temperature is T. Assume that Newton's law of cooling is applicable. The temperature of the body at the end of next 10 minutes will be
View SolutionA body cools in a surrounding which is at constant temperature of θ0. Assume that it obeys Newton's law of colling. Its temperature θ is plotted against time t. Tangents are drawn to the curve at the points P(θ=θt) and Q(θ=θ2). These tangents meet the time axis at angles of ϕ2 and ϕ1, as shown
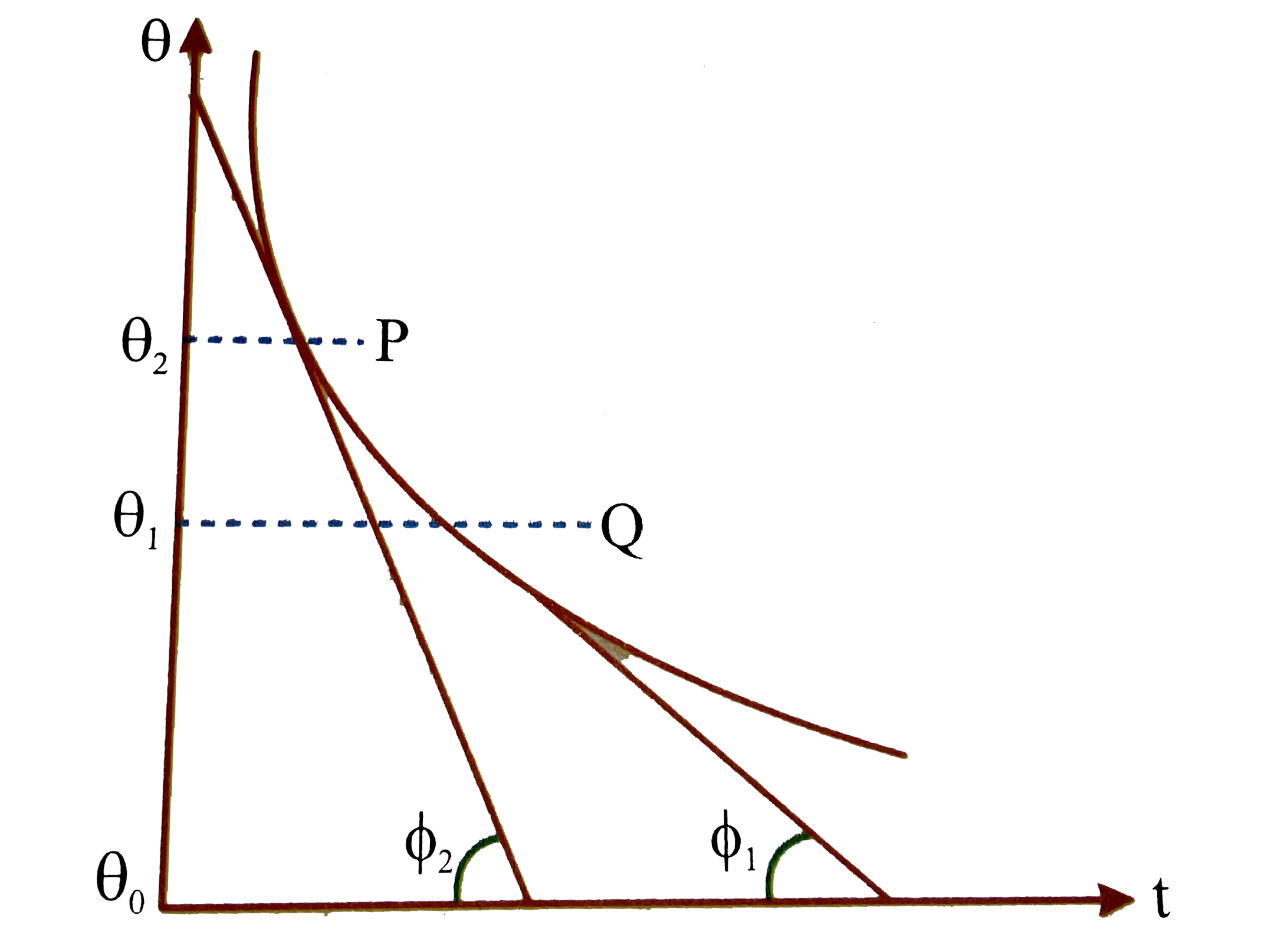 View Solution
View SolutionA body having mass 2 Kg cools in a surrounding of constant temperature 30∘C. Its heat capacity is 2J/∘C. Initial temperature of the body is 40∘C. Assume Newton's law of cooling is valid. The body cools to 36∘C in 10 minutes.
When the body temperature has reached 36∘C. it is heated again so that it reaches to 40∘C in 10 minutes. Assume that the rate of loss of heat at 38∘C is the average rate of loss for the given time . The total heat required from a heater by the body is :View SolutionTwo liquids of specific heat ratio 1:2 are at temperature 2θandθ
View SolutionFigure shows a large tank of water at a constant temperature θ0 and a small vessel containing a mass m of water at an initial temperature θ1(<θ0). A metal rod of length L, area of cross section A and thermal conductivity K connects the two vessels. Find the time taken for the temperature of the water in the smaller vessel to become θ2(θ1<θ2<θ0) . Specific heat capacity of water is s and all other heat capacities are negligible.
 View Solution
View SolutionA body cools in a surrounding of constant temperature 30∘C Its heat capacity is 2J/∘C. Initial temeprature of cooling is valid. The body cools to 38∘C in 10 min
The temperature of the body In .∘C denoted by θ. The veriation of θ versus time t is best denoted asView SolutionIn Newton's law of cooling dθdt=−k(θ−θ0) the constant k is proportional to .
View SolutionThe correct graph between the temperature of a hot body kept in cooler surrounding and time is (Assume newton's law of cooling)
View SolutionA body cools from 60∘C to 40∘C in 7 minutes. Temperature of surrounding is 10∘C. After next 7 minutes what will be its temperature ? During whole process Newton's law of cooling is obeyed.
View Solution

