A bob of mass m attached to an inextensible string of length I is suspended from a vertical support. The bob rotates in a horizontal circle with an angular speed ω red/s about the vertical. About the point of suspension:
angular momentum changes in direction but not in magnitude.
angular momentum changes both in direction and magnitude.
angular momentum is conserved.
angular momentum changes in magnitude but not in direction
To solve the problem, we need to find the angular momentum of a bob of mass m rotating in a horizontal circle about a vertical support. We will analyze the situation step by step.
Step 1: Understand the setup
We have a bob of mass m attached to a string of length l. The bob rotates in a horizontal circle with an angular speed ω radians per second. The point of suspension is labeled as point O.
Step 2: Identify the position and velocity vectors
- The position vector →r from the point of suspension O to the bob is directed from O to the bob's position in the horizontal plane.
- The velocity vector →v of the bob is tangent to the circular path in which the bob is rotating.
Step 3: Calculate the magnitude of the position vector
The magnitude of the position vector →r can be expressed as:
r=lsin(θ)
where θ is the angle between the string and the vertical.
Step 4: Calculate the magnitude of the velocity vector
The velocity v of the bob can be expressed as:
v=rω=(lsin(θ))ω
Step 5: Calculate the angular momentum
The angular momentum →L about point O is given by the formula:
→L=→r×→p
where →p=m→v is the linear momentum of the bob. Thus,
→L=→r×(m→v)
The magnitude of the angular momentum can be calculated as:
L=m⋅r⋅v
Substituting the values of r and v:
L=m⋅(lsin(θ))⋅(lsin(θ)ω)=ml2sin2(θ)ω
Step 6: Analyze the direction of angular momentum
The direction of →L can be determined using the right-hand rule. As the bob rotates, the direction of →L changes, tracing out a conical path. However, the magnitude of L remains constant since both m, l, and ω are constant.
Conclusion
The angular momentum L of the bob about the point of suspension O is constant in magnitude but changes in direction as the bob rotates.
We have a bob of mass m attached to a string of length l. The bob rotates in a horizontal circle with an angular speed ω radians per second. The point of suspension is labeled as point O.
- The position vector →r from the point of suspension O to the bob is directed from O to the bob's position in the horizontal plane.
- The velocity vector →v of the bob is tangent to the circular path in which the bob is rotating.
The magnitude of the position vector →r can be expressed as:
r=lsin(θ)
where θ is the angle between the string and the vertical.
The velocity v of the bob can be expressed as:
v=rω=(lsin(θ))ω
The angular momentum →L about point O is given by the formula:
→L=→r×→p
where →p=m→v is the linear momentum of the bob. Thus,
→L=→r×(m→v)
The magnitude of the angular momentum can be calculated as:
L=m⋅r⋅v
Substituting the values of r and v:
L=m⋅(lsin(θ))⋅(lsin(θ)ω)=ml2sin2(θ)ω
The direction of →L can be determined using the right-hand rule. As the bob rotates, the direction of →L changes, tracing out a conical path. However, the magnitude of L remains constant since both m, l, and ω are constant.
The angular momentum L of the bob about the point of suspension O is constant in magnitude but changes in direction as the bob rotates.
Topper's Solved these Questions
Similar Questions
Three balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O. Match the following columns.
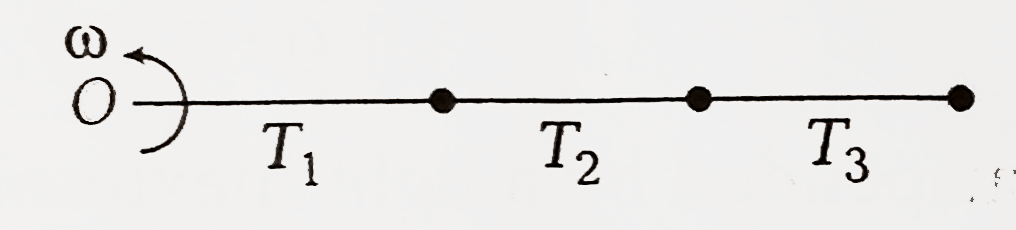
View SolutionA bob of mass m attached to an inextensible string of length l is suspended from a verticle support. The bob rotates in a horizontal circle with an angular speed ωrad/s about the verticle. About the point of suspension.
View SolutionThree balls each of mass 1 kg are attached with three strings each of length 1 m as shown in figure. They are rotated in a horizontal circle with angular velocity ω=4rad s−1 about point O.find the tensions .
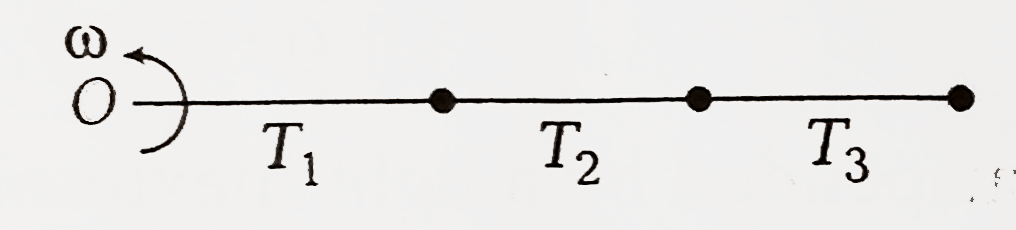
View SolutionA metal bob of mass 0.6 kg is attached to the end of a string of length 1 m and the bob is whirled in a horizontal circle with a uniform speed of 12 m/s. What is the centripetal force acting on the bob ? If the speed of the bob is 5 m/s calculate the tension in the string.
View SolutionA simple pendulum is constructed by attaching a bob of mass m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
View SolutionA simple pendulum is constructed by attaching a bob of mas m to a string of length L fixed at its upper end. The bob oscillates in a vertical circle. It is found that the speed of the bob is v when the string makes an angle θ with the vertical. Find the tension in the string at this instant.
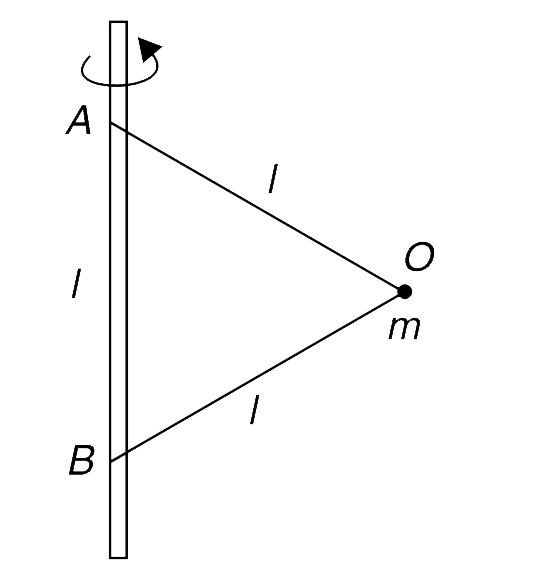
View SolutionA particle of mass m is attached to a vertical rod with two inextensible strings AO and BO of equal lengths l. Distance between A and B is also l. The setup is rotated with angular speed ω with rod as the axis.
View SolutionA bob hangs from a rigid support by an inextensible string of length l. It is released from rest when string makes an agngle 60∘ with vertical . The speed of the bob at the lowest position is
View SolutionA metal wire of length L is suspended vertically from a rigid support. When a bob of mass M is attached to the lower end of wire, the elongation of the wire is l:
View SolutionA bob of mass 1 kg is suspended from an inextensible string of length 1 m. When the string makes an angle 60∘ with vertical, speed of the bob is 4 m/s
Net acceleration of the bob at this instant is
View Solution
