For a linear plot of log (x/m) versus log [ in a Freundlich adsorption isotherm, which of the following statements is correct ? (k and n are consists)
1/n appears as the intercept.
Only 1/n appears as the slope
log (1/n) appears as the intercept.
Both k and 1/n appear in the slope term.
The correct Answer is:B
To solve the question regarding the linear plot of log(x/m) versus log(p) in the context of the Freundlich adsorption isotherm, we can follow these steps:
Step 1: Understand the Freundlich Isotherm Equation
The Freundlich adsorption isotherm is given by the equation:
x/m=kp1/n
where:
- x is the amount of adsorbate,
- m is the mass of the adsorbent,
- k is the Freundlich constant,
- p is the pressure of the adsorbate,
- n is a constant that indicates the adsorption intensity.
Step 2: Take the Logarithm of Both Sides
Taking the logarithm of both sides of the Freundlich equation gives:
log(x/m)=log(k)+1nlog(p)
Step 3: Rearranging the Equation
We can rearrange the equation to fit the linear form y=mx+c:
log(x/m)=1nlog(p)+log(k)
Here, we can identify:
- y=log(x/m)
- x=log(p)
- Slope m=1n
- Intercept c=log(k)
Step 4: Identify the Slope and Intercept
From the rearranged equation:
- The slope of the line is 1n.
- The intercept of the line is log(k).
Conclusion
Based on the analysis:
- Option A (1/n appears as an intercept) is incorrect.
- Option B (1/n appears as a slope) is correct.
- Option C (log(1/n) appears as intercept) is incorrect.
- Option D (both k and 1/n appear in the slope term) is incorrect.
Thus, the correct answer is Option B: 1/n appears as the slope.
The Freundlich adsorption isotherm is given by the equation:
x/m=kp1/n
where:
- x is the amount of adsorbate,
- m is the mass of the adsorbent,
- k is the Freundlich constant,
- p is the pressure of the adsorbate,
- n is a constant that indicates the adsorption intensity.
Taking the logarithm of both sides of the Freundlich equation gives:
log(x/m)=log(k)+1nlog(p)
We can rearrange the equation to fit the linear form y=mx+c:
log(x/m)=1nlog(p)+log(k)
Here, we can identify:
- y=log(x/m)
- x=log(p)
- Slope m=1n
- Intercept c=log(k)
From the rearranged equation:
- The slope of the line is 1n.
- The intercept of the line is log(k).
Based on the analysis:
- Option A (1/n appears as an intercept) is incorrect.
- Option B (1/n appears as a slope) is correct.
- Option C (log(1/n) appears as intercept) is incorrect.
- Option D (both k and 1/n appear in the slope term) is incorrect.
Topper's Solved these Questions
Similar Questions
Knowledge Check
For Freundlich adsorption isotherm, xm=kp1/n , the value of n is
A1. always greater than oneB2. always smaller than oneC3. always equal to oneD4. greater than one at low temperature and smaller than one at high temperature.Which of the following curves is in accordance with Freundlich adsorption isotherm ?
A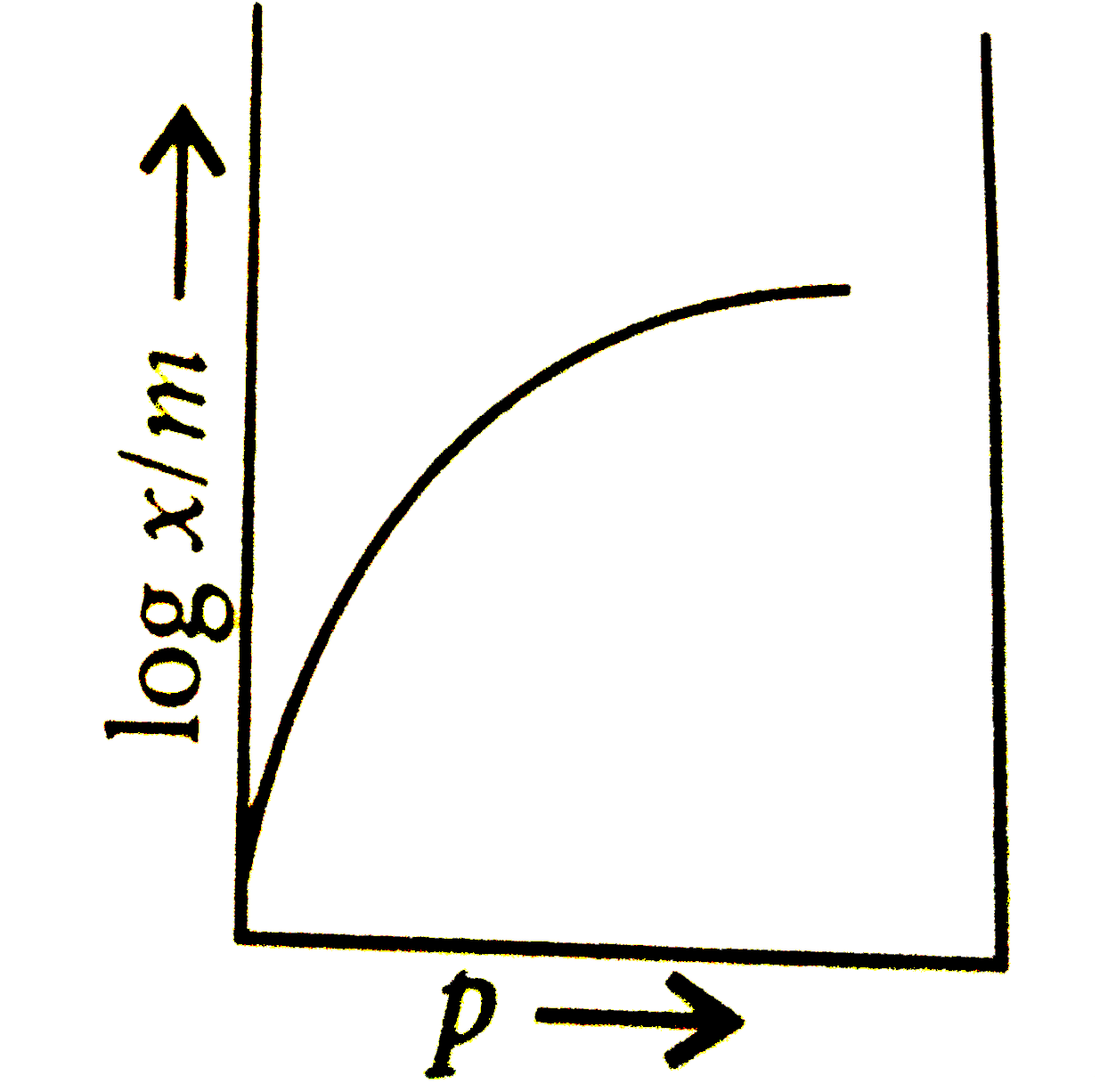 B
B C
C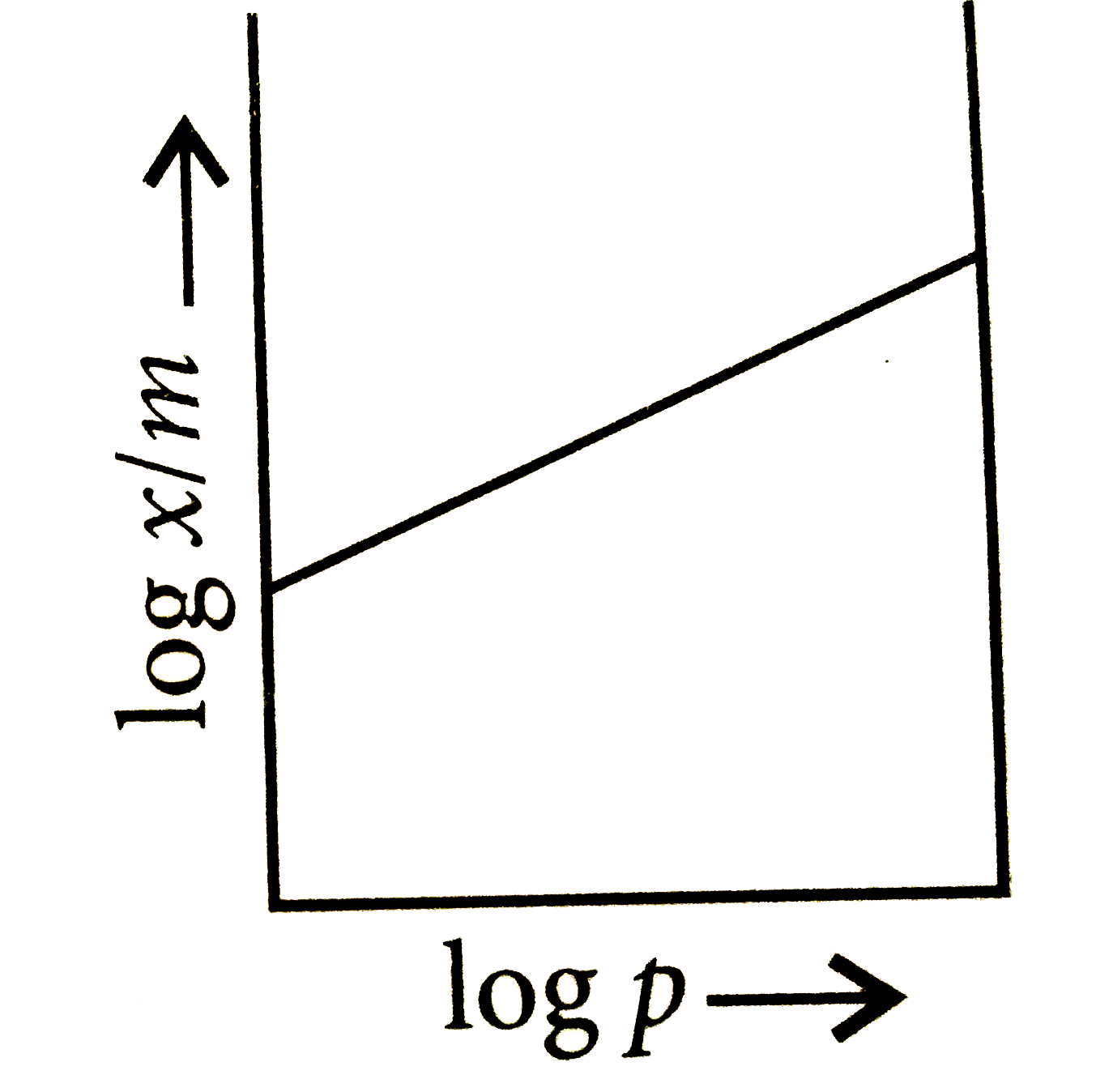 D
D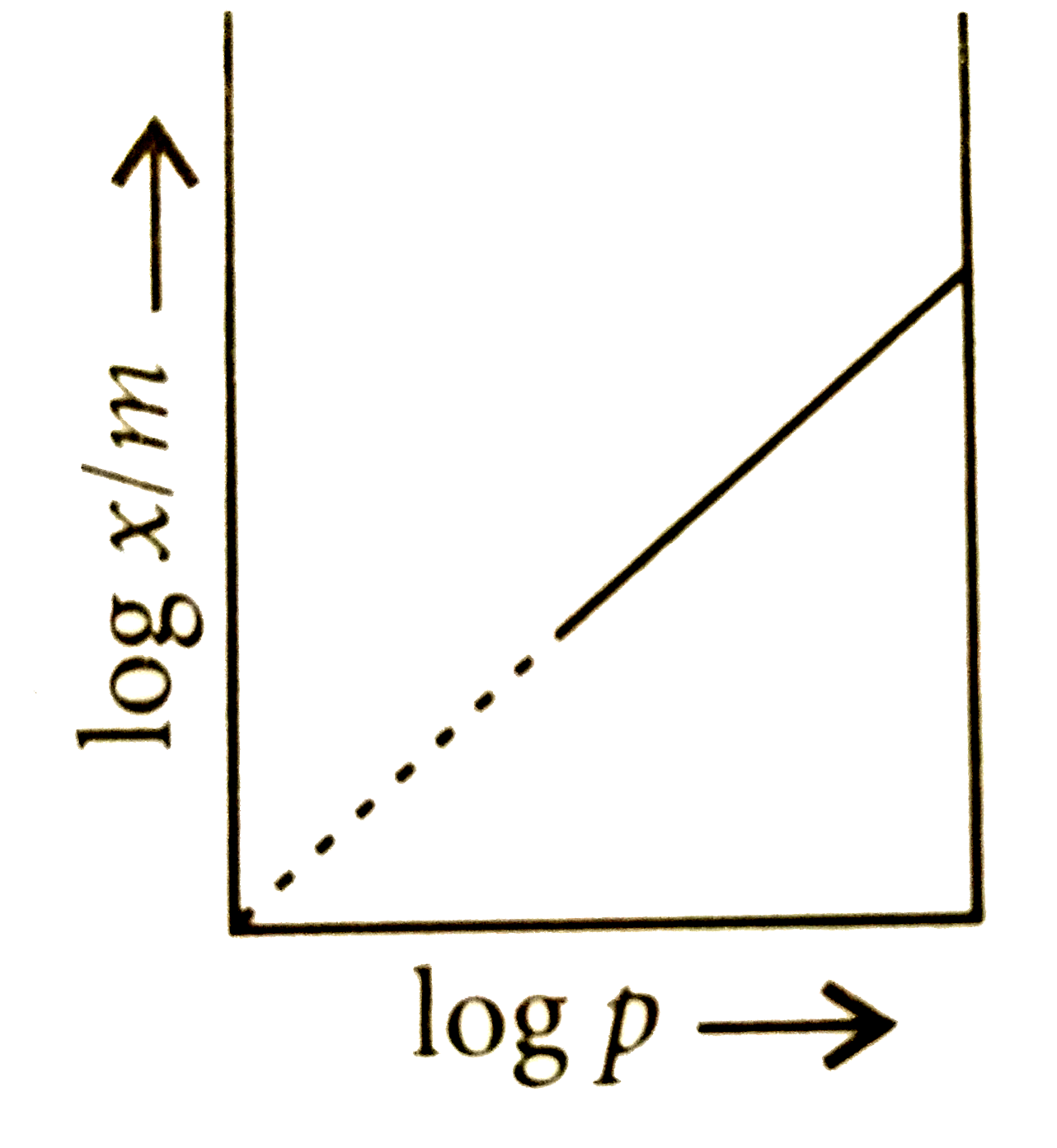
Which of the following statement is correct for the spontaneous adsorption of a gas?
View SolutionWhich of the following does not represent freundlich
adsorption isotherm?
View SolutionWhich of the following graphs represents freundlich adsorption isotherm?
View SolutionWhich of the following statements about physical adsorption is not correct?
View SolutionWhich of the plots of ln K vs (1T) is/are correct?
View SolutionA graph is plotted between log (x/m) and log p according to the equation xmkp1/n
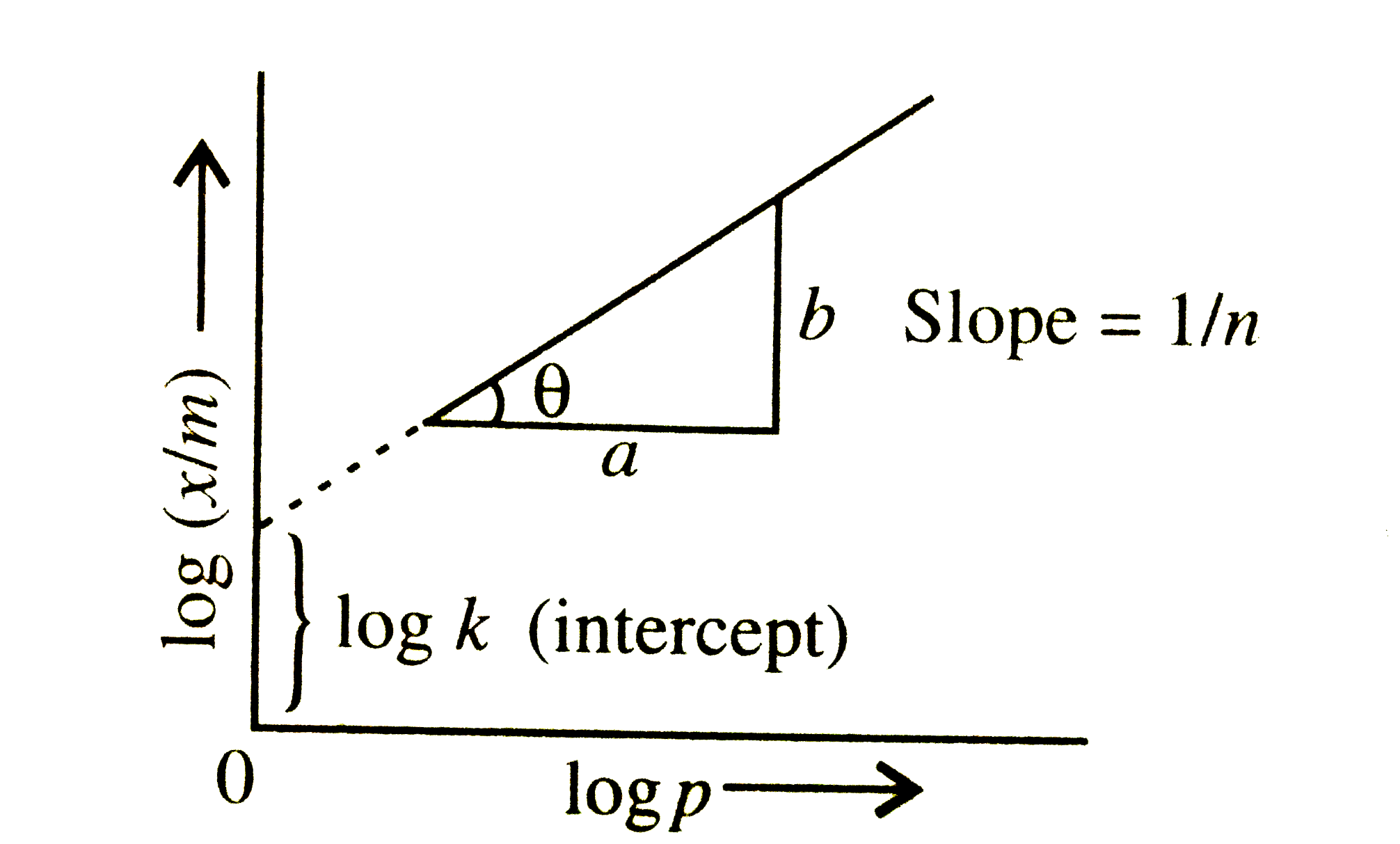
Which is the following statements about his graph is not correct ?
View Solution
