A 1 kg block attached to a spring vibrates with a frequency of 1 Hz on a frictionless horizontal table. Two springs identical to the original spring are attached in parallel to an 8 kg block placed on the same table. So, the frequency of vibration of the 8 kg block is
2 Hz
14 Hz
12√2Hz
12 Hz
The correct Answer is:D
To solve the problem, we need to analyze the relationship between the mass of the block, the spring constant, and the frequency of vibration.
1. Understand the Frequency Formula:
The frequency f of a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass.
2. Initial Conditions:
For the 1 kg block vibrating with a frequency of 1 Hz:
f1=1 Hz,m1=1 kg
We can express the spring constant k using the frequency:
1=12π√k1
Squaring both sides gives:
1=k4π2⟹k=4π2
3. New Conditions:
Now, we have an 8 kg block with two identical springs attached in parallel. The equivalent spring constant k′ when two springs are in parallel is:
k′=2k
Therefore:
k′=2×4π2=8π2
The mass m2 is:
m2=8 kg
4. Calculate the New Frequency:
Using the new mass and the new spring constant in the frequency formula:
f2=12π√k′m2=12π√8π28=12π√π2=12π⋅π=12 Hz
5. Final Answer:
The frequency of vibration of the 8 kg block is:
f2=0.5 Hz
The frequency f of a mass-spring system is given by the formula:
f=12π√km
where k is the spring constant and m is the mass.
For the 1 kg block vibrating with a frequency of 1 Hz:
f1=1 Hz,m1=1 kg
We can express the spring constant k using the frequency:
1=12π√k1
Squaring both sides gives:
1=k4π2⟹k=4π2
Now, we have an 8 kg block with two identical springs attached in parallel. The equivalent spring constant k′ when two springs are in parallel is:
k′=2k
Therefore:
k′=2×4π2=8π2
The mass m2 is:
m2=8 kg
Using the new mass and the new spring constant in the frequency formula:
f2=12π√k′m2=12π√8π28=12π√π2=12π⋅π=12 Hz
The frequency of vibration of the 8 kg block is:
f2=0.5 Hz
Topper's Solved these Questions
Similar Questions
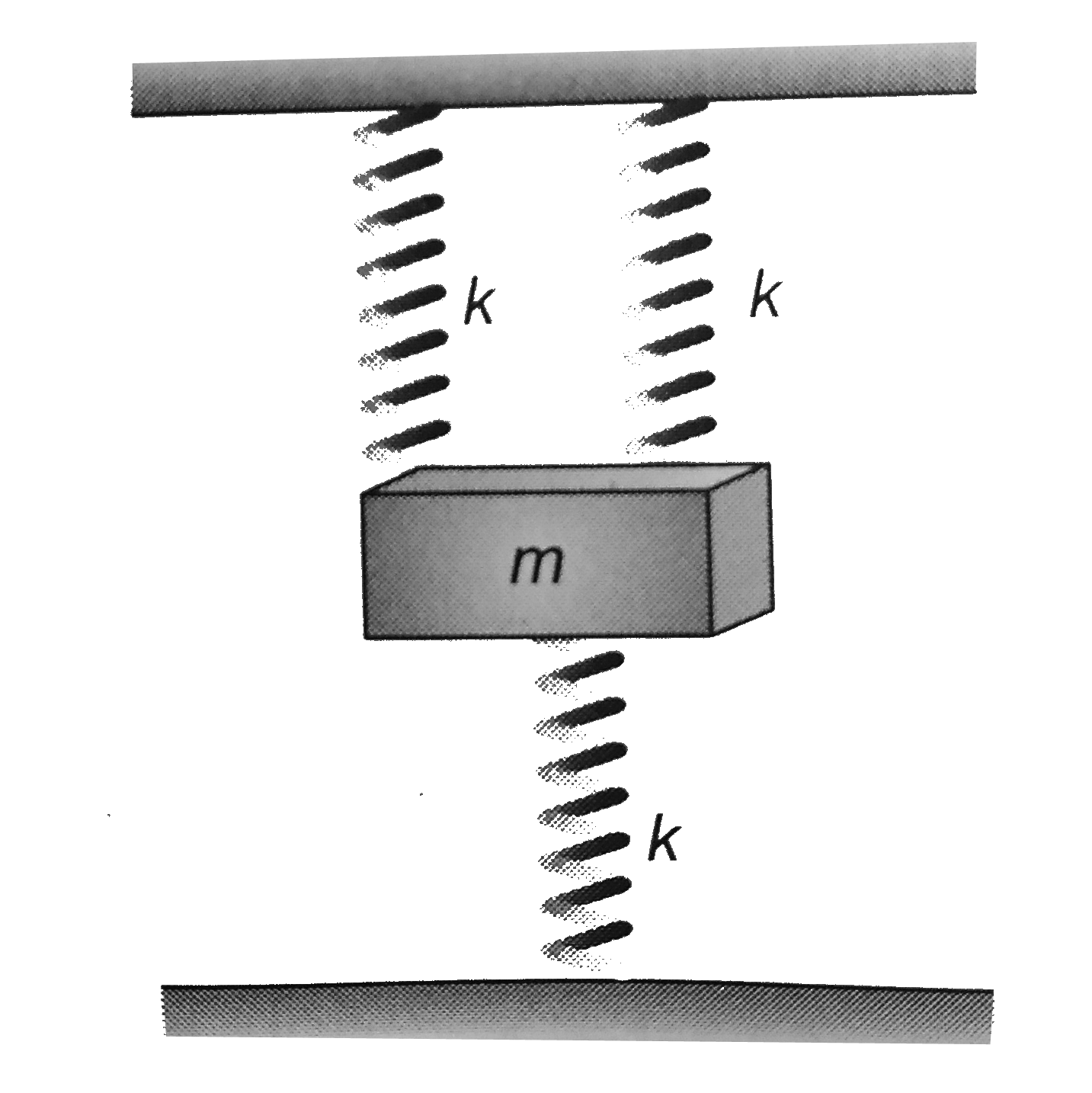
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
View SolutionThe time period of oscillations of a block attached to a spring is t1. When the spring is replaced by another spring, the time period of the block is t2. If both the springs are connected in series and the block is made to oscillate using the combination, then the time period of the block is
View SolutionTwo spring are connected toa block of mass M placed a frictionless surface as shown if both the spring have a spring constant k the frequency of oscillation block is

View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Find the velocity of the block when spring acquires its natural length
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionA block of mass 2kg is attached with a spring of spring constant 4000Nm−1 and the system is kept on smooth horizontal table. The other end of the spring is attached with a wall. Initially spring is stretched by 5cm from its natural position and the block is at rest. Now suddenly an impulse of 4kg−ms−1 is given to the block towards the wall.
Approximate distance travelled by the block when it comes to rest for a second time (not including the initial one) will be (Take √45=6.70)
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionA block of mass m, attached to a spring of spring constant k, oscilltes on a smooth horizontal table. The other end of the spring is fixed to a wall. If it has speed v when the spring is at its naturla lenth, how far will it move on the table before coming to an instantaneous rest?
View SolutionA mass of 1kg attached to the bottom of a spring has a certain frequency of vibration. The following mass has to be added to it in order to reduce the frequency by half :
View SolutionIn the arrangement shown in figure , find the ratio of tension in the strings attached with 4kg block and the with 1kg block

View Solution
