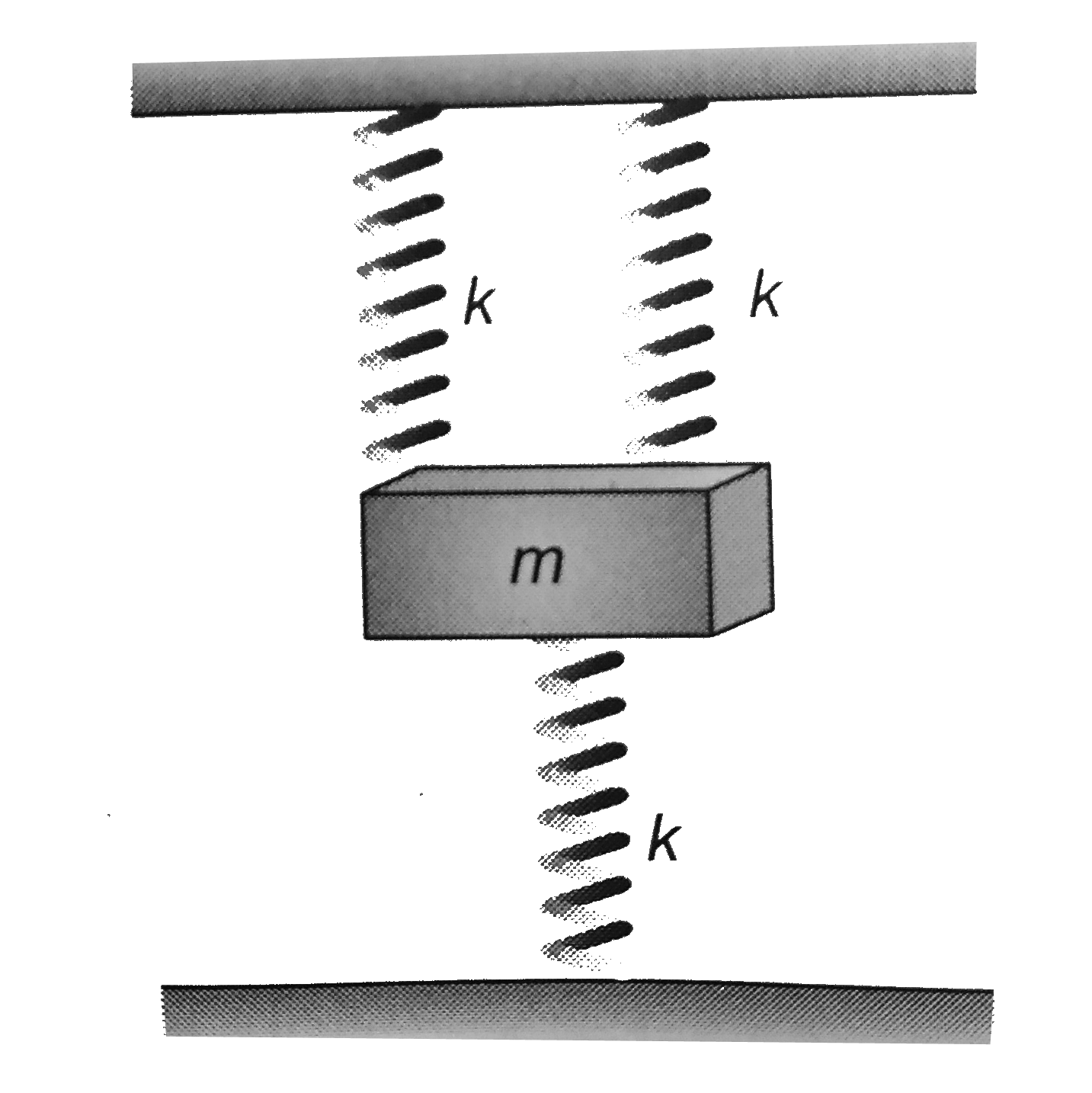
In the figure all spring are identical having spring constant k and mass m each The block also mass m The frequency of oscillation of the block is
12π√3km
12π√3km
2π√3m3k
None of these
The correct Answer is:B
In the ………….
If spring has the mass then :
f=12π
⎷km+Mspring3
Spring equivalent =3k (As all are in parallel)
∴f=12π
⎷3km+(3m)3
⇒f=12π√3k2m
Topper's Solved these Questions
- TEST PAPERSBOOK - RESONANCE ENGLISHCHAPTER - TEST PAPERSEXERCISE - PART - II PHYSICS
106 Videos
- SIMPLE HARMONIC MOTION BOOK - RESONANCE ENGLISHCHAPTER - SIMPLE HARMONIC MOTION EXERCISE - Advanced Level Problems
13 Videos
- TEST SERIESBOOK - RESONANCE ENGLISHCHAPTER - TEST SERIESEXERCISE - PHYSICS
130 Videos
Similar Questions
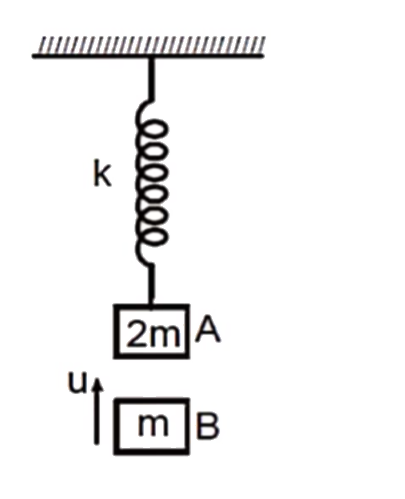
A block A of mass 2m is hanging from a vertical massless spring of spring constant k and is in equilibrium. Another block B of mass m strikes the block A with velocity u and sticks to it as shown in the figure. The magnitude of the acceleration of the combined system of the blocks just after the collision is
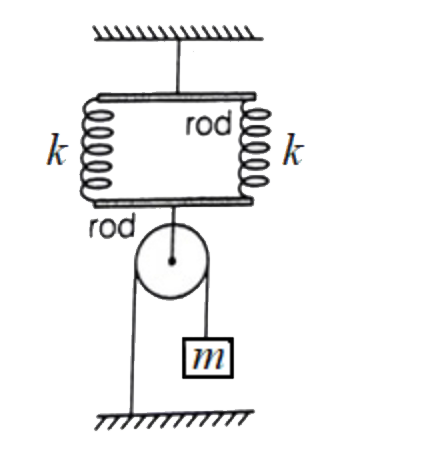
View SolutionThere are two identical spring each of spring constant k. here springs, pulley and rods are massless and the block has mass m . What is the extension of each spring at equilibrium?
View Solution
Knowledge Check
A system of springs with their spring constants are as shown in figure. What is the frequency of oscillations of the mass m ?
 A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k4]mB12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mC12π√k1k2(k3+k4)[(k1+k2)+(k3+k4)+k1k2]mD12π√(k1+k2)(k3+k4)+k1k2k1k2(k3+k4)m
A rod of length l and mass m, pivoted at one end, is held by a spring at its mid - point and a spring at far end. The spring have spring constant k. Find the frequency of small oscillations about the equilibrium position.

View SolutionAssertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
View SolutionAssertion : In spring block system if length of spring and mass of block both are halved, then angular frequency of oscillations will remain unchanged.
Reason : Angular frequency is given by ω=√km .
View SolutionTwo identical springs of spring constant k are attached to a block of mass m and to fixed supports as shown in the figure. The time period of oscillation is

View SolutionIn figure, the stiffness of the spring is k and mass of the block is m. The pulley is fixed. Initially, the block m is held such that the elongation in the spring is zero and then released from rest. Find:
a. the maximum elongation in the spring.
b. the maximum speed of the block m. Neglect the mass of the spring and that of the string. Also neglect the friction.
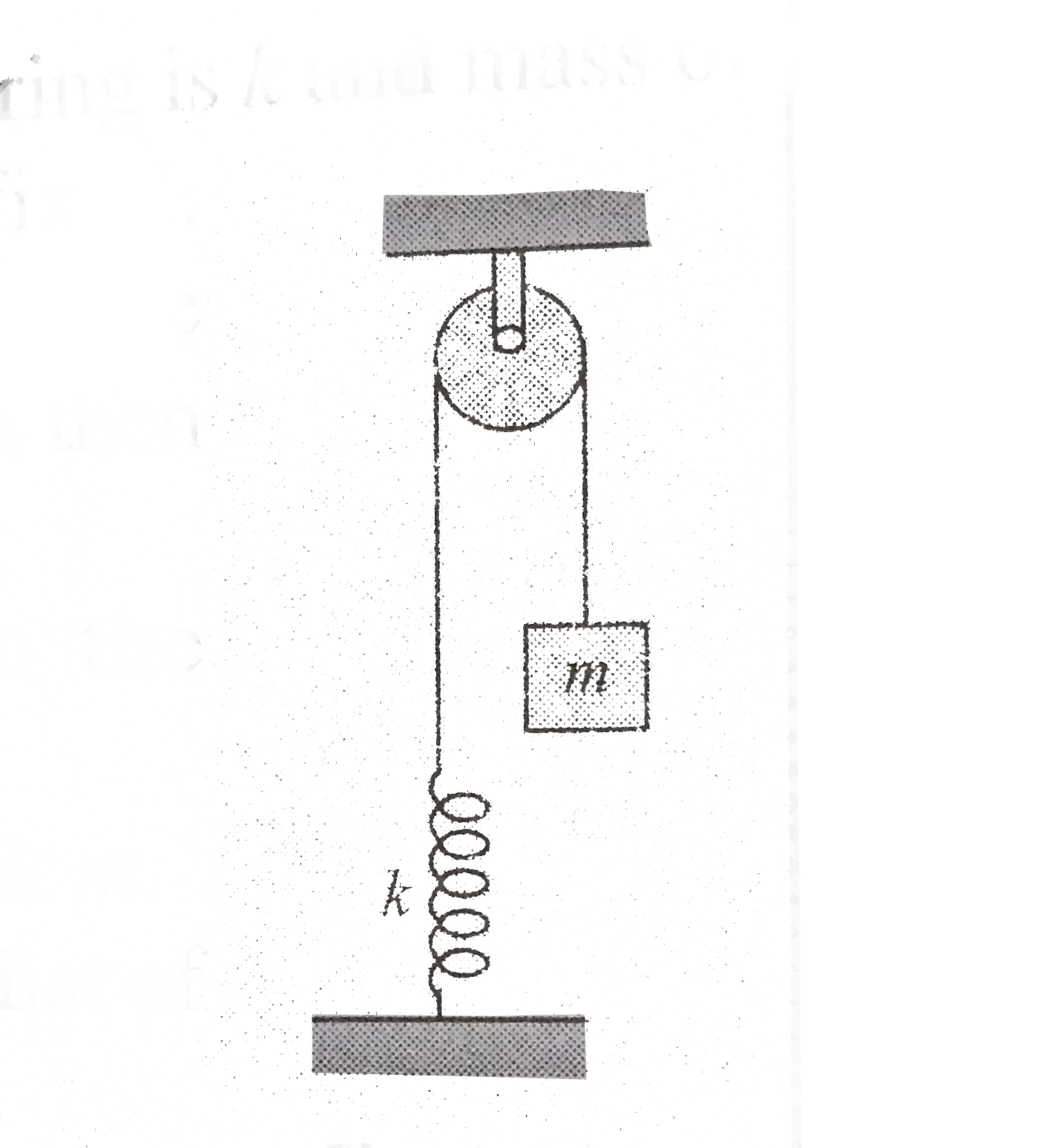
View SolutionA block of mass 20 kg is hung with the help of ideal string, pulleys and spring (Spring constant k = 1000 N/m) as shown in figure. If block is in equilibrium position then extension in the spring will be (g=10ms−2)
View SolutionA block of mass m is connected with two ideal pullies and a massless spring of spring constant K as shown in figure. The block is slightly displaced from its equilibrium position. If the time period of oscillation is μπ√mK. Then find the value of μ.

View Solution
