Two batteries with emf 12 V and 13V are connected in parallel across a load resistor of 10Ω . The internal resistances of the two batteries are 1Ωand2Ω respectively . The voltage across the load lies between
11.7 V and 11.8 V
11.6 V and 11.7 V
11.5 V and 11.6 V
11.4 V and 11.5 V
The correct Answer is:C
To solve the problem of finding the voltage across the load resistor when two batteries are connected in parallel, we will follow these steps:
Step 1: Identify the Given Values
- EMF of Battery 1 (E1) = 12 V
- Internal Resistance of Battery 1 (R1) = 1 Ω
- EMF of Battery 2 (E2) = 13 V
- Internal Resistance of Battery 2 (R2) = 2 Ω
- Load Resistance (R_load) = 10 Ω
Step 2: Calculate the Equivalent Internal Resistance
When batteries are connected in parallel, the equivalent internal resistance (R_eq) can be calculated using the formula:
Req=R1⋅R2R1+R2
Substituting the values:
Req=1⋅21+2=23Ω
Step 3: Calculate the Equivalent EMF
The equivalent EMF (E_eq) for batteries connected in parallel with different EMFs can be calculated using the formula:
Eeq=E1R1+E2R2
We need to find the total current flowing through the circuit, which is given by:
I=EeqReq+Rload
To find E_eq, we first calculate the contributions of each battery:
Eeq=121+132⋅23
Calculating this gives:
Eeq=12+6.5=18.5V
Step 4: Calculate the Total Resistance in the Circuit
The total resistance in the circuit (R_total) is the sum of the equivalent internal resistance and the load resistance:
Rtotal=Req+Rload=23+10=23+303=323Ω
Step 5: Calculate the Current in the Circuit
Using Ohm's Law, we can find the current (I) flowing through the circuit:
I=EeqRtotal=18.5323=18.5⋅332=55.532≈1.734375A
Step 6: Calculate the Voltage Across the Load Resistor
The voltage (V_load) across the load resistor can be calculated using Ohm's Law:
Vload=I⋅Rload=1.734375⋅10≈17.34375V
Step 7: Determine the Range of Voltage Across the Load
Since the voltage across the load lies between the voltages provided by the two batteries, we can conclude that:
- The voltage across the load will be between the lower voltage (from the weaker battery) and the higher voltage (from the stronger battery).
Final Answer
The voltage across the load lies between approximately 11.57 V and 12.33 V.
- EMF of Battery 1 (E1) = 12 V
- Internal Resistance of Battery 1 (R1) = 1 Ω
- EMF of Battery 2 (E2) = 13 V
- Internal Resistance of Battery 2 (R2) = 2 Ω
- Load Resistance (R_load) = 10 Ω
When batteries are connected in parallel, the equivalent internal resistance (R_eq) can be calculated using the formula:
Req=R1⋅R2R1+R2
Substituting the values:
Req=1⋅21+2=23Ω
The equivalent EMF (E_eq) for batteries connected in parallel with different EMFs can be calculated using the formula:
Eeq=E1R1+E2R2
We need to find the total current flowing through the circuit, which is given by:
I=EeqReq+Rload
To find E_eq, we first calculate the contributions of each battery:
Eeq=121+132⋅23
Calculating this gives:
Eeq=12+6.5=18.5V
The total resistance in the circuit (R_total) is the sum of the equivalent internal resistance and the load resistance:
Rtotal=Req+Rload=23+10=23+303=323Ω
Using Ohm's Law, we can find the current (I) flowing through the circuit:
I=EeqRtotal=18.5323=18.5⋅332=55.532≈1.734375A
The voltage (V_load) across the load resistor can be calculated using Ohm's Law:
Vload=I⋅Rload=1.734375⋅10≈17.34375V
Since the voltage across the load lies between the voltages provided by the two batteries, we can conclude that:
- The voltage across the load will be between the lower voltage (from the weaker battery) and the higher voltage (from the stronger battery).
The voltage across the load lies between approximately 11.57 V and 12.33 V.
Topper's Solved these Questions
Similar Questions
The cell has an emf of 2V and the internal resistance of this cell is 0.1Ω, it is connected to resistance of 3.9Ω, the voltage across the cell will be
View SolutionA battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
View SolutionA generator has an EMF of 440 V and internal resistance of 400 ohm . Its terminals are connected to a load of 4000 ohm , the voltage across the load is
View SolutionThe series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View SolutionThe series combination of two batteries, both of the same emf 10 V, but different internal resistance of 10Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R (in Ω ) is : _________.
View SolutionThe series combination of two batteries both of the same emf 10 V, but different internal resistance of 20Ω and 5Ω is connected to the parallel combination of two resistors 30Ω and RΩ . The voltage difference across the battery of internal resistance 20Ω is zero, the value of R(in Ω) is __________.
View SolutionThe figure shows two capacitors connected in parallel with two resistance and a battery of emf 10V , internal resistance 5Ω. At steady state.
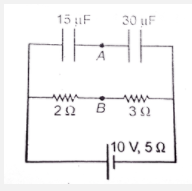
View SolutionThe series combination of two batteries, both of the same emf 20 V, but different internal resistance of 10 Ω and 2 Ω , is connected to the parallel combination of two resistors 10 ohm and RΩ . The voltage difference across the battery of internal resistance 10Ω is zero, the value of R(∈Ω) is _________.
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
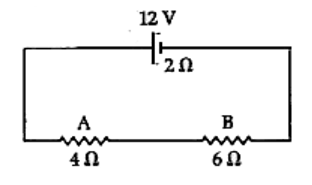
Find The potential difference across 6 Ω Resistor.
View SolutionA battery of emf 2 V and internal resistance r is connected in series with a resistor of 10Ω through an ammeter of resistance 2Ω. The ammeter reads 50 mA. Draw the circuit diagram and calculate the value of r.
View Solution
