A battery of EMF E produces currents 4 A and 3 A when connected to external resistance 1Ω and 2Ω respectively. The internal resistance of the battery is
0.5Ω
2Ω
1.5Ω
1Ω
The correct Answer is:B
To find the internal resistance of the battery, we can use the information given about the currents produced when connected to different external resistances.
1. Identify the Given Information:
- When connected to an external resistance of R1=1Ω, the current I1=4A.
- When connected to an external resistance of R2=2Ω, the current I2=3A.
2. Apply Ohm's Law:
The relationship between the EMF E, internal resistance r, and the external resistance R is given by:
I=ER+r
where I is the current flowing through the circuit.
3. Set Up the Equations:
For the first case with R1=1Ω:
4=E1+r(Equation 1)
For the second case with R2=2Ω:
3=E2+r(Equation 2)
4. Express EMF E in terms of r:
From Equation 1:
E=4(1+r)=4+4r(1)
From Equation 2:
E=3(2+r)=6+3r(2)
5. Set the Two Expressions for E Equal:
Since both expressions equal E:
4+4r=6+3r
6. Solve for r:
Rearranging the equation:
4r−3r=6−4
r=2Ω
7. Conclusion:
The internal resistance of the battery is r=2Ω.
- When connected to an external resistance of R1=1Ω, the current I1=4A.
- When connected to an external resistance of R2=2Ω, the current I2=3A.
The relationship between the EMF E, internal resistance r, and the external resistance R is given by:
I=ER+r
where I is the current flowing through the circuit.
For the first case with R1=1Ω:
4=E1+r(Equation 1)
For the second case with R2=2Ω:
3=E2+r(Equation 2)
From Equation 1:
E=4(1+r)=4+4r(1)
From Equation 2:
E=3(2+r)=6+3r(2)
Since both expressions equal E:
4+4r=6+3r
Rearranging the equation:
4r−3r=6−4
r=2Ω
The internal resistance of the battery is r=2Ω.
Topper's Solved these Questions
Similar Questions
A battery supplies 150W and 196 W power to two resistance of 6Ω and 4Ω when they are connected separately to it. The internal resistance of the battery is:-
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA current of 2A flows through a 2Ω resistor when connected across a battery. The same battery supplies a current of 0.5A when connected across a 9Ω resistor. The internal resistance of the battery is
View SolutionA cell supplies a current of 2 A when it is connected to a 5Ω resistance and supplies a current of 1.2 A, if it is connected to a resistance of 9 Ω. Find the e.m.f and internal resistance of the cell.
View SolutionA cell of e.m.f. ε and internal resistance r sends a current of 1.0 A when it is connected to an external resistance of 1.9 Ω. But it sends a current of 0.5 A when it is connected to an resistance of 3.9Ω calculate the values of ε and r .
View SolutionWhen a battery connected across a resistor of 16Ω, the voltage across the resistor is 12 V. When the same battery is connected across a resistor of 10Ω, voltage across it is 11 V. The internal resistance of the battery (in ohm) is
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
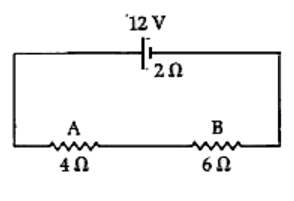
Find Electrical energy spent per minute in 4 Ω Resistor.
View SolutionA battery of e.m.f. 12 V and internal resistance 2 Ω is connected with two resistors A and B of resistance 4 Ω and 6 Ω respectively joined in series.
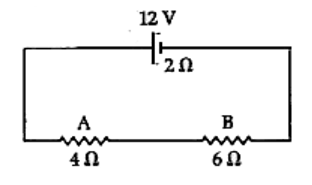
Find The potential difference across 6 Ω Resistor.
View SolutionA battery of e.m.f. 15 V and internal resistance 3Ω is connected to two resistors 3 Ω and 6 Ω connected in parallel. Find :
the current through the battery,
View SolutionA galvanometer having 50 divisions provided with a variable shunt S is used to measure the current when connected in series with a resistance of 90Ω and a battery of internal resistance 10Ω. It is observed that when the shunt resistances are 10Oemga and 50Ω, the deflections are, respectively, 9 and 30 divisions. What is the resistance of the galvanometer
View Solution
