On interchanging the resistances, the balance point of a meter bridge shifts to the left by 10 cm. The resistance of their series combination is 1kΩ. How much was the resistance on the left slot before interchanging the resistances?
910Ω
990Ω
505Ω
550Ω
The correct Answer is:D
To solve the problem, we need to find the resistance in the left slot before interchanging the resistances using the information provided.
1. Understanding the Problem:
We have a meter bridge where two resistances R1 and R2 are connected. When these resistances are interchanged, the balance point shifts by 10 cm. The total resistance of the series combination is given as R1+R2=1000Ω.
2. Setting Up the Initial Conditions:
Let the initial balance point be at a distance x cm from the left end. Therefore, the distance from the right end will be 100−x cm.
3. Applying the Wheatstone Bridge Principle:
For the initial configuration, we can write:
R1⋅(100−x)=R2⋅x(1)
4. After Interchanging the Resistances:
After interchanging R1 and R2, the new balance point shifts to x−10 cm. Hence, the new distances are x−10 cm from the left and 100−(x−10)=110−x cm from the right. We can write:
R2⋅(110−x)=R1⋅(x−10)(2)
5. Dividing the Two Equations:
To eliminate the resistances, we divide equation (1) by equation (2):
R1⋅(100−x)R2⋅(110−x)=R2⋅xR1⋅(x−10)
This simplifies to:
(100−x)(110−x)=x(x−10)
6. Cross-Multiplying:
Cross-multiplying gives:
(100−x)(x−10)=x(110−x)
7. Expanding Both Sides:
Expanding both sides:
100x−1000−x2+10x=110x−x2
Simplifying this leads to:
110x−100x+1000−10x=0
0=0
Thus, we can rearrange to find:
210x=1100
8. Solving for x:
Dividing both sides by 210:
x=1100210≈52.38cm
9. Finding the Ratio of Resistances:
Now, using the ratio of resistances:
R1R2=x100−x=52.3847.62≈119
10. Calculating R1:
Since R1+R2=1000Ω, we can express R1 and R2:
R1=1120×1000=550Ω
R2=920×1000=450Ω
Thus, the resistance on the left slot before interchanging the resistances was 550 Ω.
We have a meter bridge where two resistances R1 and R2 are connected. When these resistances are interchanged, the balance point shifts by 10 cm. The total resistance of the series combination is given as R1+R2=1000Ω.
Let the initial balance point be at a distance x cm from the left end. Therefore, the distance from the right end will be 100−x cm.
For the initial configuration, we can write:
R1⋅(100−x)=R2⋅x(1)
After interchanging R1 and R2, the new balance point shifts to x−10 cm. Hence, the new distances are x−10 cm from the left and 100−(x−10)=110−x cm from the right. We can write:
R2⋅(110−x)=R1⋅(x−10)(2)
To eliminate the resistances, we divide equation (1) by equation (2):
R1⋅(100−x)R2⋅(110−x)=R2⋅xR1⋅(x−10)
This simplifies to:
(100−x)(110−x)=x(x−10)
Cross-multiplying gives:
(100−x)(x−10)=x(110−x)
Expanding both sides:
100x−1000−x2+10x=110x−x2
Simplifying this leads to:
110x−100x+1000−10x=0
0=0
Thus, we can rearrange to find:
210x=1100
Dividing both sides by 210:
x=1100210≈52.38cm
Now, using the ratio of resistances:
R1R2=x100−x=52.3847.62≈119
Since R1+R2=1000Ω, we can express R1 and R2:
R1=1120×1000=550Ω
R2=920×1000=450Ω
Topper's Solved these Questions
Similar Questions
In a wheatstone bridge resistance of each of the four sides is 10Ω. If the resistance of the galvanometer is also 10Ω , then effective resistance of the bridge will be
View SolutionThe resistance of each arm of the wheat stone bridge is 10Ω. A resistance of 10Ω is connected in series with galvanometer then the equivalent resistance across the battery will be:-
View Solution
Knowledge Check
In series combination of resistances :
Ap.d. is same across each resistanceBtotal resistance is reducedCcurrent is same in each resistanceDall above are true.In the series combination of two or more than two resistances
Athe current through each resistance is sameBthe voltage through each resistance is sameCneither current nor voltage through each resistance is sameDboth current and voltage through each resistance are same
The resistance of a series combination of the resistance is S. when they are joined in parallel equvalent resistance is P. Find the value of (S2P)
View SolutionA resistance of 2Ω is connected across one gap of a meter bridge (the length of the wire is 100cm) and an unknown resistance, greater than 2Ωis conneted across the other gap. When these resistances are interchanged, the balance point shifts by 20cm. Neglecting any corrections,the unknown resistance is
View SolutionWhy is the meter bridge suitable for resistance of moderate values only ?
View SolutionTwo unknown resistances are connected in two gaps of a meter-bridge. The null point is obtained at 40 cm from left end. A 30Ω resistance is connected in series with the smaller of the two resistances, the null point shifts by 20 cm to the right end. The value of smaller resistance in Ω is
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is
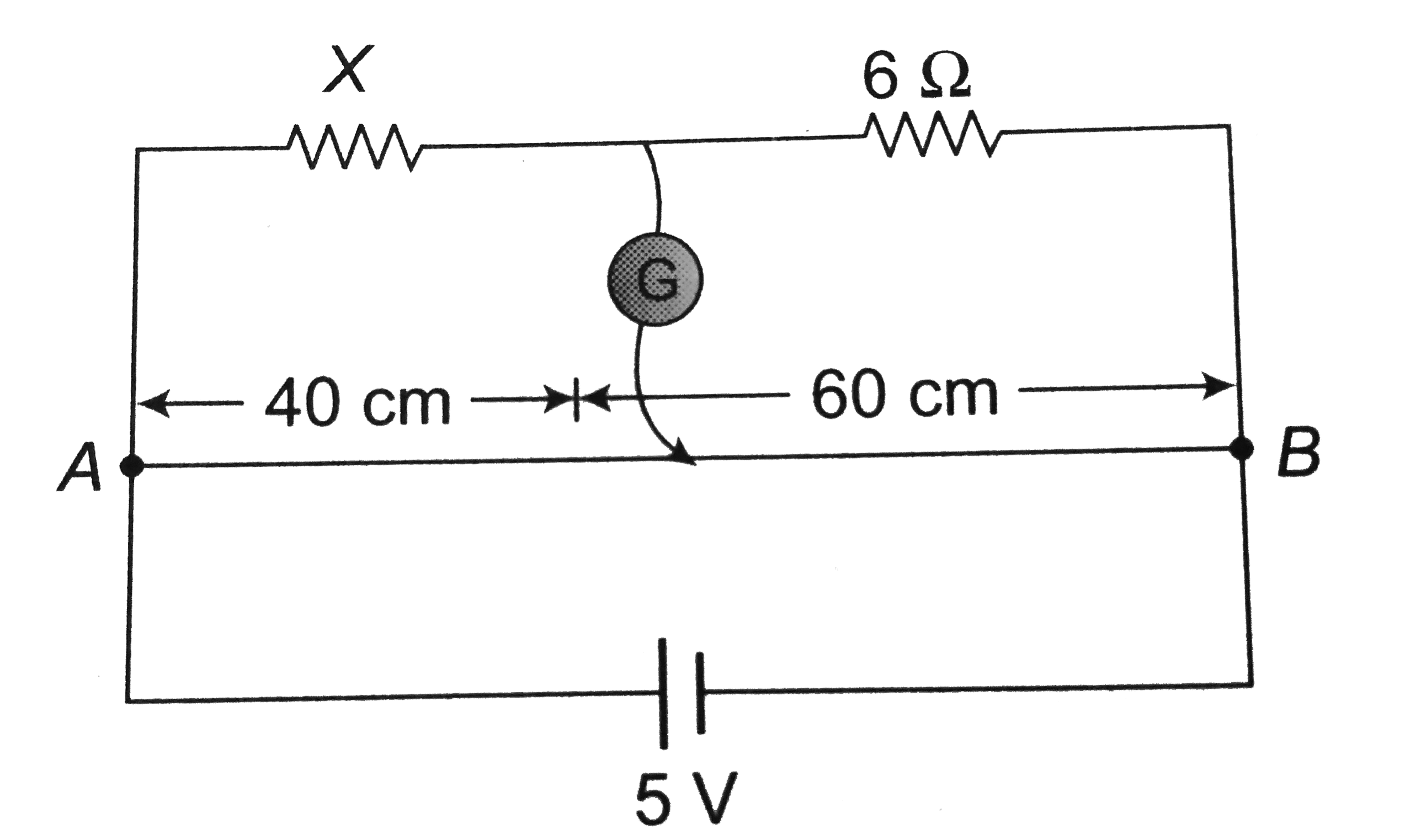
View SolutionIn the circuit shown, a meter bridge is in its balanced state. The meter bridge wire has a resistance .1ohm/cm. The value of unknown resistance X and the current drawn from the battery of negligible resistance is

View Solution
