A particle is moving in a circular path of radius a under the action of an attractive potential . Its total energy is :
Zero
The correct Answer is:D
To find the total energy of a particle moving in a circular path under the influence of the given potential U=−k2r2, we will follow these steps:
Step 1: Determine the Force from the Potential Energy
The force F associated with a potential energy U is given by:
F=−dUdr
Given U=−k2r2, we differentiate it with respect to r:
dUdr=ddr(−k2r2)=−k2⋅ddr(r−2)=−k2⋅(−2r−3)=kr3
Thus, the force is:
F=−dUdr=−kr3
Step 2: Relate the Force to Centripetal Force
For a particle moving in a circular path of radius a, the centripetal force required to keep the particle in circular motion is given by:
Fcentripetal=mv2a
Setting the attractive force equal to the centripetal force, we have:
mv2a=ka3
Rearranging gives:
mv2=ka2
Step 3: Calculate the Kinetic Energy
The kinetic energy KE of the particle is given by:
KE=12mv2
Substituting mv2 from the previous step:
KE=12⋅ka2=k2a2
Step 4: Calculate the Potential Energy
The potential energy U at radius a is:
U=−k2a2
Step 5: Calculate the Total Energy
The total energy E of the system is the sum of kinetic energy and potential energy:
E=KE+U
Substituting the values we found:
E=k2a2−k2a2=0
Final Result
Thus, the total energy of the particle is:
0
The force F associated with a potential energy U is given by:
F=−dUdr
Given U=−k2r2, we differentiate it with respect to r:
dUdr=ddr(−k2r2)=−k2⋅ddr(r−2)=−k2⋅(−2r−3)=kr3
Thus, the force is:
F=−dUdr=−kr3
For a particle moving in a circular path of radius a, the centripetal force required to keep the particle in circular motion is given by:
Fcentripetal=mv2a
Setting the attractive force equal to the centripetal force, we have:
mv2a=ka3
Rearranging gives:
mv2=ka2
The kinetic energy KE of the particle is given by:
KE=12mv2
Substituting mv2 from the previous step:
KE=12⋅ka2=k2a2
The potential energy U at radius a is:
U=−k2a2
The total energy E of the system is the sum of kinetic energy and potential energy:
E=KE+U
Substituting the values we found:
E=k2a2−k2a2=0
Thus, the total energy of the particle is:
0
Topper's Solved these Questions
Similar Questions
A particle is moving in a circular path of radius r. The displacement after half a circle would be
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
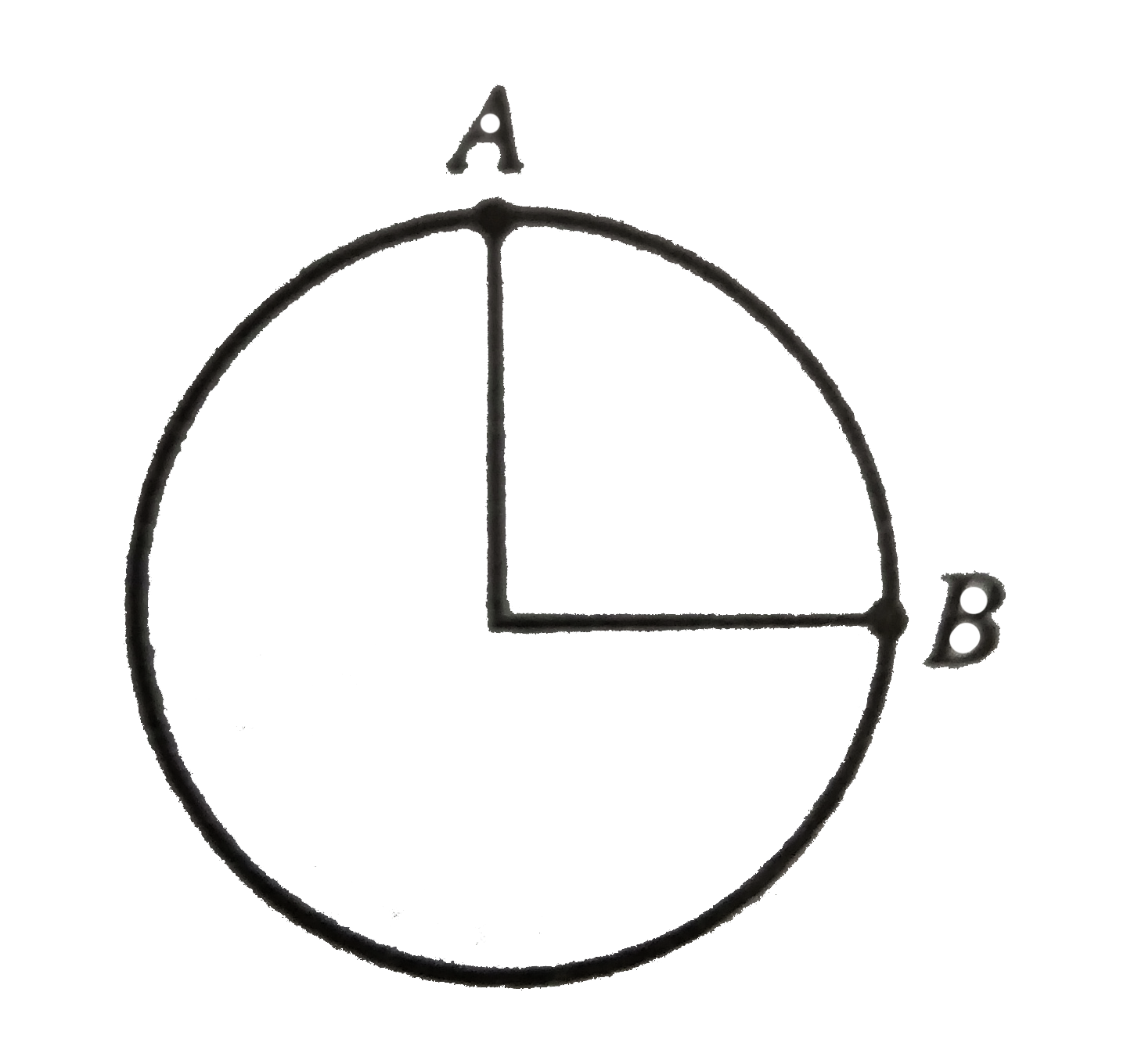
View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
View SolutionA particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionStatement 1: A charged particle is moving in a circular path under the action of a uniform magnetic field as shown in Fig. During motion kinetic energy of charged particle is costant.
Statement 2: During the motion, magnetic force acting on the particle is perpendicular to instantaneous velocity.

View SolutionA particle is moving on a circular path with constant speed, then its acceleration will be constant in
View SolutionA body moves in a circular orbit of radius R under the action of a central force. Potential due to the central force is given by V(r) = kr (k is a positive constant). Period of revolution of the body is proportional to-
View SolutionAn artificial satellite moving in circular orbit around the earth has total (kinetic + potential) energy E0. Its potential energy and kinetic energy respectively are :
View Solution
