A particle is moving in a circular path of radius r under the action of a force F. If at an instant velocity of particle is v, and speed of particle is increasing, then
→F.→v=0
→F.→v>0
→F.→v<0
→F.→v≥0
The correct Answer is:B
To solve the problem, we need to analyze the motion of a particle moving in a circular path under the influence of a force F. Given that the speed of the particle is increasing, we can derive the relationship between the force vector F and the velocity vector v.
1. Understanding the Motion:
The particle is moving in a circular path of radius r. The velocity v is tangential to the circular path, and there is a centripetal acceleration ac directed towards the center of the circle.
2. Components of Acceleration:
Since the speed of the particle is increasing, there is also a tangential acceleration at in the direction of the velocity vector v. The total acceleration a can be expressed as:
a=at+ac
where ac is directed towards the center of the circular path.
3. Direction of Force:
According to Newton's second law, the net force F acting on the particle is equal to the mass m of the particle multiplied by its total acceleration:
F=ma
The force F will have components in both the tangential direction (due to at) and the radial direction (due to ac).
4. Dot Product of Force and Velocity:
We need to evaluate the dot product F⋅v. The dot product can be expressed as:
F⋅v=|F||v|cosθ
where θ is the angle between the force vector F and the velocity vector v.
5. Analyzing the Angle:
Since the speed is increasing, the tangential component of the force F must be in the same direction as the velocity v. This means that the angle θ between F and v is between 0∘ and 90∘. Therefore, cosθ is positive.
6. Conclusion:
Since both |F| and |v| are positive and cosθ>0, we conclude that:
F⋅v>0
Thus, the correct answer is Option 2: F⋅v>0.
The particle is moving in a circular path of radius r. The velocity v is tangential to the circular path, and there is a centripetal acceleration ac directed towards the center of the circle.
Since the speed of the particle is increasing, there is also a tangential acceleration at in the direction of the velocity vector v. The total acceleration a can be expressed as:
a=at+ac
where ac is directed towards the center of the circular path.
According to Newton's second law, the net force F acting on the particle is equal to the mass m of the particle multiplied by its total acceleration:
F=ma
The force F will have components in both the tangential direction (due to at) and the radial direction (due to ac).
We need to evaluate the dot product F⋅v. The dot product can be expressed as:
F⋅v=|F||v|cosθ
where θ is the angle between the force vector F and the velocity vector v.
Since the speed is increasing, the tangential component of the force F must be in the same direction as the velocity v. This means that the angle θ between F and v is between 0∘ and 90∘. Therefore, cosθ is positive.
Since both |F| and |v| are positive and cosθ>0, we conclude that:
F⋅v>0
Thus, the correct answer is Option 2: F⋅v>0.
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - C)
80 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - D)
13 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - Assignment (SECTION - A)
64 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass M moves with constant speed along a circular path of radius r under the action of a force F. Its speed is
View SolutionA particle is moving in a circular path of radius 1 m. under the action of a centripetal force, the speed √2πms−1 of the particle is constant. Find the average of the velocity (inms−1) between A and B.
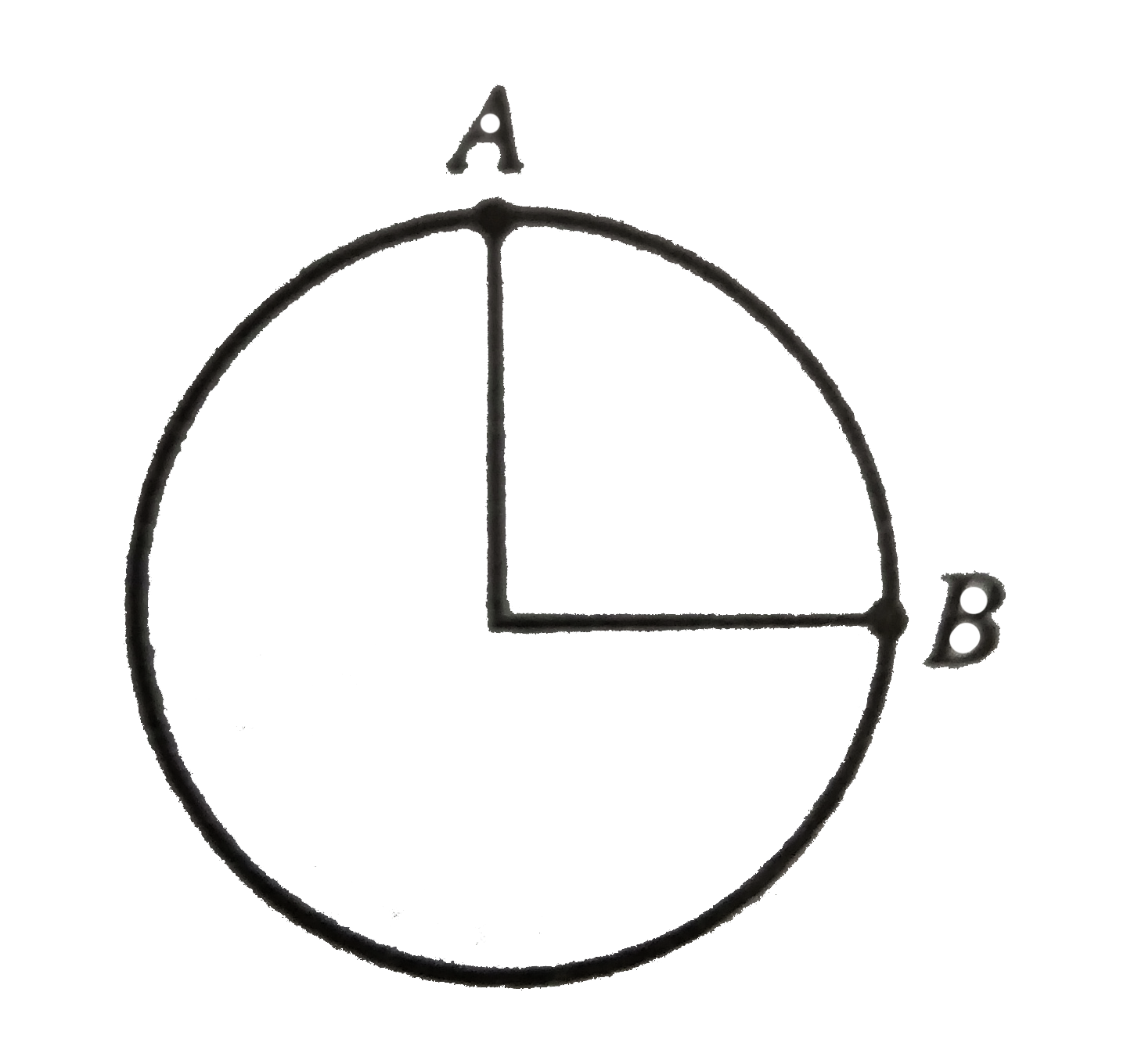
View Solution
Knowledge Check
A particle is moving on a circular path of radius R with constant speed v. During motion of the particle form point A to point B
 AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
AAverage speed is v/2BThe magnitude of average velocity is v/πCThe magnitude of average acceleration is 2v2πRDAverage velocity is zero.
A particle is moving in a circular path of radius a under the action of an attractive potential U=−k2r2. Its total energy is :
View SolutionA particle is moving in a circular path of radius r. The displacement after half a circle would be
View SolutionA particle moves in a circular path with a uniform speed. Its motion is
View SolutionA particle is revolving in a circular path of radius 2 m with constant angular speed 4 rad/s. The angular acceleration of particle is
View Solution
A particle is moving on a circular path of radius r with uniform velocity v. The change in velocity when the particle moves from P to Q is (∠POQ=40∘)
View SolutionA particle of mass m is moving on a circular path of radius r with uniform speed v , rate of change of linear momentum is
View SolutionA particle is moving on a circular path of radius 1 m with 2 m/s. If speed starts increasing at a rate of 2m/s2, then acceleration of particle is
View Solution
