A body of mass 2 kg slides down with an acceleration of 3 m/s2 on a rough inclined plane having a slope of 30∘ The external force required to take the same body up the plane with the same acceleration will be : (g=10m/s2)
6 N
20 N
4 N
4 N
To solve the problem, we need to determine the external force required to move a body of mass 2 kg up a rough inclined plane at an angle of 30 degrees with an acceleration of 3 m/s². We will follow these steps:
Step 1: Calculate the gravitational force acting on the body
The gravitational force (weight) acting on the body can be calculated using the formula:
Fg=m⋅g
Where:
- m=2kg (mass of the body)
- g=10m/s2 (acceleration due to gravity)
Calculating:
Fg=2kg⋅10m/s2=20N
Step 2: Determine the component of gravitational force along the incline
The component of the gravitational force acting down the incline can be calculated using:
Fg∥=Fg⋅sin(θ)
Where:
- θ=30∘
Calculating:
Fg∥=20N⋅sin(30∘)=20N⋅12=10N
Step 3: Calculate the frictional force
Since the body is sliding down with an acceleration of 3 m/s², we can use Newton's second law to find the frictional force. The net force acting on the body while sliding down is given by:
Fnet=m⋅a
Where:
- a=3m/s2
Calculating:
Fnet=2kg⋅3m/s2=6N
The net force acting down the incline can also be expressed as:
Fnet=Fg∥−Ffriction
Thus,
6N=10N−Ffriction
Rearranging gives:
Ffriction=10N−6N=4N
Step 4: Calculate the external force required to move the body up the incline
When moving the body up the incline with the same acceleration of 3 m/s², the forces acting on the body are:
1. The applied external force F (up the incline)
2. The gravitational force component Fg∥ (down the incline)
3. The frictional force Ffriction (down the incline)
Using Newton's second law for upward motion:
F−Fg∥−Ffriction=m⋅a
Substituting the known values:
F−10N−4N=6N
Rearranging gives:
F=10N+4N+6N=20N
Final Answer
The external force required to take the body up the plane with the same acceleration is:
20N
The gravitational force (weight) acting on the body can be calculated using the formula:
Fg=m⋅g
Where:
- m=2kg (mass of the body)
- g=10m/s2 (acceleration due to gravity)
Fg=2kg⋅10m/s2=20N
The component of the gravitational force acting down the incline can be calculated using:
Fg∥=Fg⋅sin(θ)
Where:
- θ=30∘
Fg∥=20N⋅sin(30∘)=20N⋅12=10N
Since the body is sliding down with an acceleration of 3 m/s², we can use Newton's second law to find the frictional force. The net force acting on the body while sliding down is given by:
Fnet=m⋅a
Where:
- a=3m/s2
Fnet=2kg⋅3m/s2=6N
Fnet=Fg∥−Ffriction
Thus,
6N=10N−Ffriction
Rearranging gives:
Ffriction=10N−6N=4N
When moving the body up the incline with the same acceleration of 3 m/s², the forces acting on the body are:
1. The applied external force F (up the incline)
2. The gravitational force component Fg∥ (down the incline)
3. The frictional force Ffriction (down the incline)
F−Fg∥−Ffriction=m⋅a
Substituting the known values:
F−10N−4N=6N
F=10N+4N+6N=20N
The external force required to take the body up the plane with the same acceleration is:
20N
Topper's Solved these Questions
Similar Questions
A block of mass m slides down a rough inclined plane with an acceleration g2

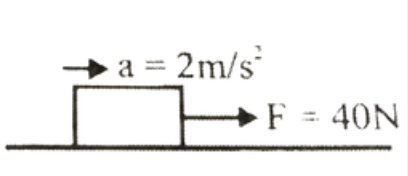
View SolutionA block of mass 10 kg, moving with acceleration 2m/s2 on horizontal rough surface is shown in figure
View SolutionDerive an expression for the acceleration of a body sliding down a rough inclined plane.
View SolutionThe frictional force of the air on the body of mass 0.25kg, falling with an acceleration of 9.2 m/s2 will be (g=9.8m/s2).
View SolutionA balloon os mass 2 KG is rising up with an acceleration of 4ms2 . The upward force acting on the balloon is (g = 10 ms^-2)
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30∘ with the horizontal. If co-efficient of friciton between the surface of contact of the body and the plane is 0.25. Find the least force required to pull the body up.
View SolutionA solid cylinder of mass 3kg is placed on a rough inclined plane of inclination 30∘. If g=10ms2, then the minimum frictional force required for it to roll without slipping down the plane is

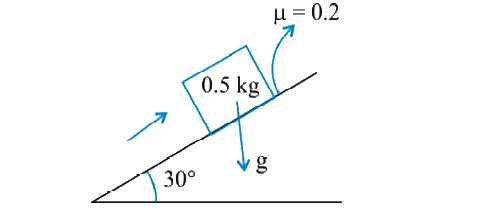
View SolutionA block of mass 0.5 kg is kept on a rough inclined plane making an angle of 30∘ with horizontal. What power will be required to move the block up the plane (along the plane) with a velocity of 5m/s ? (Take m = 0.2 between block and plane)
View SolutionA body of mass 10kg is on a rough inclined plane having an inclination of 30° with the horizontal. If coefficient of friction between the surfaces of contact of the body and the plane is 0.5. Find the least force required to pull the body up the plane.
View SolutionA block of mass m=3kg slides on a rough inclined plane of cofficient of friction 0.2 Find the resultant force offered by the plane on the block

View Solution
