A balloon os mass 2 KG is rising up with an acceleration of 4ms2 . The upward force acting on the balloon is (g = 10 ms^-2)
0.8 kgf
2.8 kgf
2.4 kgf
2.0 kgf
The correct Answer is:b
To solve the problem, we need to find the upward force acting on the balloon. We can use Newton's second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration.
1. Identify the given values:
- Mass of the balloon (m) = 2 kg
- Acceleration of the balloon (a) = 4 m/s²
- Acceleration due to gravity (g) = 10 m/s²
2. Calculate the weight of the balloon:
The weight (W) of the balloon acts downward and is given by the formula:
W=m⋅g
Substituting the values:
W=2kg⋅10m/s2=20N
3. Apply Newton’s second law:
According to Newton's second law, the net force (F_net) acting on the balloon can be expressed as:
Fup−W=m⋅a
where Fup is the upward force acting on the balloon. Rearranging the equation gives:
Fup=W+m⋅a
4. Substitute the known values into the equation:
Now, substituting the values we have:
Fup=20N+(2kg⋅4m/s2)
Fup=20N+8N=28N
5. Convert the force to kg-force:
To express the force in kg-force, we divide by the acceleration due to gravity (g):
Fup=28N10m/s2=2.8kg-force
Final Answer:
The upward force acting on the balloon is 2.8 kg-force.
---
- Mass of the balloon (m) = 2 kg
- Acceleration of the balloon (a) = 4 m/s²
- Acceleration due to gravity (g) = 10 m/s²
The weight (W) of the balloon acts downward and is given by the formula:
W=m⋅g
Substituting the values:
W=2kg⋅10m/s2=20N
According to Newton's second law, the net force (F_net) acting on the balloon can be expressed as:
Fup−W=m⋅a
where Fup is the upward force acting on the balloon. Rearranging the equation gives:
Fup=W+m⋅a
Now, substituting the values we have:
Fup=20N+(2kg⋅4m/s2)
Fup=20N+8N=28N
To express the force in kg-force, we divide by the acceleration due to gravity (g):
Fup=28N10m/s2=2.8kg-force
The upward force acting on the balloon is 2.8 kg-force.
Topper's Solved these Questions
Similar Questions
A balloon of mass 10 kg is raising up with an acceleration of 20ms−2. If a mass of 4 kg is removed from the balloon its acceleration becomes ( take, g=10ms−2)
View SolutionA ballon of mass m is rising up with an acceleration a show that the fraction og weight of balloon that must be detached in order to double its acceleration , assuming the upthrust of air to remain the same
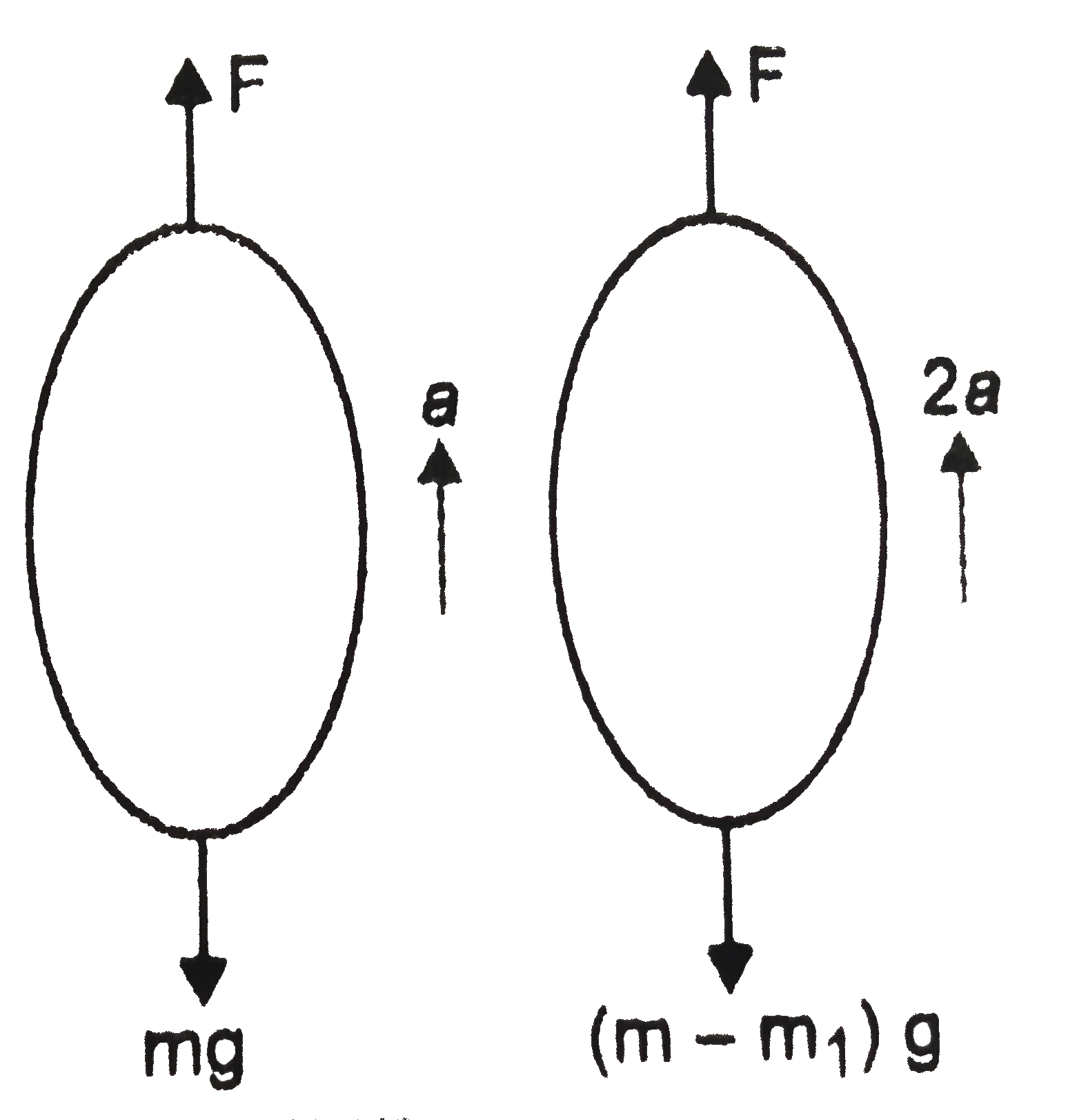
View Solution
Knowledge Check
A stone of mass 1 kg is lying on the floor of a train which is accelerating with 1ms−2. The net force acting on the stone is
AzeroB1NC5ND10N
A bird of mass 0.1 kg rising vertically with an acceleration 0.2ms−2. The muscular force exerted by it is (g=9.8ms−2)
(a) 1 Newton
(b) 9.8 kg,wt
(c ) 1/9.8 kg.wt
(d) 980 newtons.
View SolutionA balloon starts rising from the ground with an acceleration of 1.25 m/s2 . A stone is released from the balloon after 10s. Determine
(1) maximum height of ston from ground
(2) time taken by stone to reach the ground
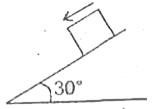
View SolutionA block of mass 10 kg is released on rough incline plane. Block start descending with acceleration 2m/s2. Kinetic friction force acting on block is (take g=10m/s2)
View SolutionA man in a balloon throws a stone downwards with a speed of 5m/s with respect to balloon. The balloon is moving upwards with a constant acceleration of 5m/s2. Then velocity of the stone relative to the man after 2 seconds is.

View SolutionA man in a balloon, rising vertically with an acceleration of 5m/s2, releases a ball 10 s after the balloon is let go from the ground. The greatest height above the ground reached by the ball is
View SolutionA lift of mass 200 kg is moving upward with an acceleration of 3m/s2 . If g=10m/s2 then the tension of string of the lift will be :
View SolutionA balloon rises up with constant net acceleration of 10m/s2. After 2 s a particle drops from the balloon. After further 2 s match the following : (Takeg=10m/s2)
Column IColumn II(A)Height of perticle from ground(p)Zero(B)Speed of particle(q)10SIunits(C)Displacement of Particle(r)40SIunits(D)Acceleration of particle(s)20SIunits
View Solution