A proton of mass m collides elastically with a particle of unknown mass at rest After the collision the proton and the unknwon particle are seen moving at an angle fo 90∘ with respect to each other The mass of unknown particle is :
2m
m2
m√3
m
To solve the problem, we need to analyze the elastic collision between the proton and the unknown particle. Here’s a step-by-step breakdown of the solution:
Step 1: Understand the Initial Conditions
- A proton of mass m is moving with some initial velocity v towards an unknown particle of mass M which is at rest.
- The proton collides elastically with the unknown particle.
Hint: Remember that in elastic collisions, both momentum and kinetic energy are conserved.
Step 2: Analyze the Collision
- After the collision, the proton and the unknown particle move at an angle of 90∘ to each other.
- Let’s denote the velocity of the proton after the collision as v′ and the velocity of the unknown particle as u.
Hint: Visualize the situation by drawing a diagram showing the initial and final velocities of both particles.
Step 3: Apply Conservation of Momentum
- The conservation of momentum states that the total momentum before the collision equals the total momentum after the collision.
- Before the collision:
Total initial momentum=mv+M⋅0=mv
- After the collision:
Total final momentum=mv′+Mu
Setting the two equal gives:
mv=mv′+Mu
Hint: Write down the momentum equations for both the x and y components separately.
Step 4: Apply Conservation of Kinetic Energy
- In elastic collisions, kinetic energy is also conserved:
12mv2=12m(v′)2+12Mu2
Hint: Remember to simplify the equation by canceling out the 12 factor.
Step 5: Use the Geometry of the Situation
- Since the velocities after the collision are at 90∘ to each other, we can use the Pythagorean theorem:
v′2+u2=v2
Hint: This relationship comes from the fact that the resultant velocity before the collision equals the vector sum of the velocities after the collision.
Step 6: Solve the Equations
- From the momentum equation, we can express M in terms of m:
M=m(v−v′)u
- Substitute u from the kinetic energy equation into this equation and simplify.
Step 7: Conclude the Mass Relationship
- After solving the equations, we find that for the velocities to satisfy both momentum and energy conservation, the mass of the unknown particle must equal the mass of the proton:
M=m
Final Answer
The mass of the unknown particle is m.
---
- A proton of mass m is moving with some initial velocity v towards an unknown particle of mass M which is at rest.
- The proton collides elastically with the unknown particle.
- After the collision, the proton and the unknown particle move at an angle of 90∘ to each other.
- Let’s denote the velocity of the proton after the collision as v′ and the velocity of the unknown particle as u.
- The conservation of momentum states that the total momentum before the collision equals the total momentum after the collision.
- Before the collision:
Total initial momentum=mv+M⋅0=mv
- After the collision:
Total final momentum=mv′+Mu
mv=mv′+Mu
- In elastic collisions, kinetic energy is also conserved:
12mv2=12m(v′)2+12Mu2
- Since the velocities after the collision are at 90∘ to each other, we can use the Pythagorean theorem:
v′2+u2=v2
- From the momentum equation, we can express M in terms of m:
M=m(v−v′)u
- Substitute u from the kinetic energy equation into this equation and simplify.
- After solving the equations, we find that for the velocities to satisfy both momentum and energy conservation, the mass of the unknown particle must equal the mass of the proton:
M=m
The mass of the unknown particle is m.
Topper's Solved these Questions
Similar Questions
A particle of mass m collides with a stationary particle and continues to move at an angle of 45∘ with respect to the original direction . The second particle also recoils at an angle of 45∘ to this direction . The mass of the second particle is (collision is elastic )
View SolutionA particle of mass m moving with speed V collides elastically with another particle of mass 2m. Find speed of smaller mass after head on collision
View SolutionA particle of mass m moving with speed u collides perfectly inelastically with another particle of mass 3 m at rest. Loss of KE of system in the collision is
View SolutionA particle of mass m with an initial velocity uˆi+2uˆj collides with a particle of mass 3m at rest. After collision, the two particles stick together and the combined particle moves with a velocity vˆi+v'ˆj. Which of the following is incorrect?
View SolutionA particle of mass m moving towards west with speed v collides with another particle of mass m movies towards south. If two particles st ich t o each other the speed of the new particle of mass 2 m will be
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA smooth sphere of mass M moving with velocity u directly collides elastically with another sphere of mass m at rest. After collision their final velocities are V and v respectively. The value of v is
View SolutionA particle of mass m is moving along the x-axis with speed v when It collides with a particle of mass 2m initially at rest. After the collision, the first particle has come to rest and the second particle has split into two equal-mass pieces that are shown in the figure. Which of the following statements correctly describes the speeds of the two places? (θ>0)
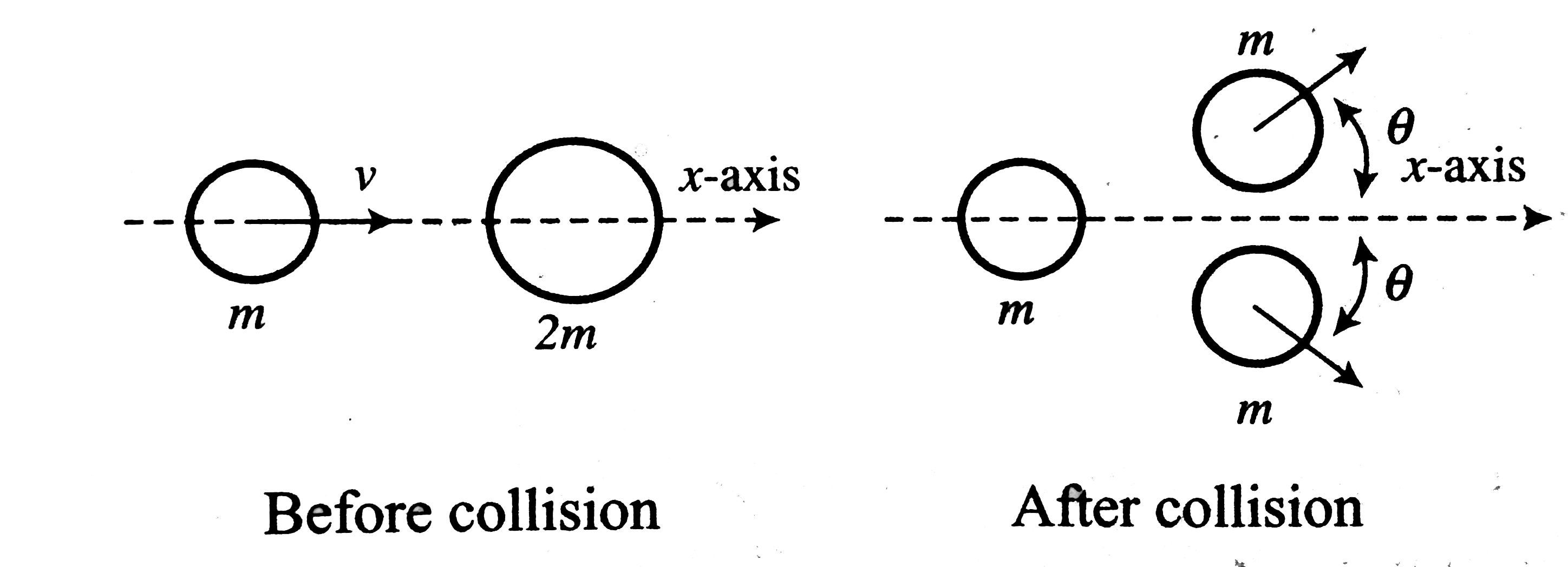
View SolutionA particle of mass m collides with another stationary particle of mass M such that the second particle starts moving and the first particle stops just after the collision. Then which of the following conditions must always be valid ?
View SolutionA particle A of mass m initially at rest slides down a height of 1.25 m on a frictionless ramp, collides with and sticks to an identical particles B of mass m at rest as shown in the figure.

Then, particles A and B together collide elastically with particle G of mass 2m at rest. The speed of particle G after the collision with combined body (A+B) would be (Take, g=10ms−2)
View Solution
