A man grows into a giant such that his linear dimension increase by a factor of 9. Assuming that his density remains same, the stress in the leg will change by a factor of
81
1/9
9
1/81
The correct Answer is:D
To solve the problem, we need to determine how the stress in the leg of a man changes when his linear dimensions increase by a factor of 9, while maintaining the same density.
1. Understanding Stress:
Stress (σ) is defined as the force (F) acting on an area (A):
σ=FA
2. Force Acting on the Body:
The force acting on the man's leg due to gravity is the weight, which can be expressed as:
F=mg
where m is the mass of the man and g is the acceleration due to gravity.
3. Expressing Mass in Terms of Density:
The mass can be expressed in terms of density (ρ) and volume (V):
m=ρV
4. Volume in Terms of Linear Dimensions:
The volume of a three-dimensional object is proportional to the cube of its linear dimension:
V∝L3
Therefore, if the linear dimension increases by a factor of 9, the new volume (V2) can be expressed as:
V2=93V1=729V1
5. Area in Terms of Linear Dimensions:
The cross-sectional area (A) is proportional to the square of the linear dimension:
A∝L2
6. Calculating Stress:
Now we can express the initial and final stress:
σ1=F1A1=m1gA1
σ2=F2A2=m2gA2
7. Relating Initial and Final States:
Since the density remains constant, we have:
m1=ρV1andm2=ρV2=ρ(729V1)
Thus, the new mass is:
m2=729m1
8. Area Change:
The area also changes according to the square of the linear dimension:
A2=92A1=81A1
9. Final Stress Calculation:
Now substituting these into the stress equations:
σ1=m1gA1
σ2=729m1g81A1=72981⋅m1gA1=9σ1
10. Conclusion:
The stress in the leg changes by a factor of 9.
Final Answer:
The stress in the leg will change by a factor of 9.
Stress (σ) is defined as the force (F) acting on an area (A):
σ=FA
The force acting on the man's leg due to gravity is the weight, which can be expressed as:
F=mg
where m is the mass of the man and g is the acceleration due to gravity.
The mass can be expressed in terms of density (ρ) and volume (V):
m=ρV
The volume of a three-dimensional object is proportional to the cube of its linear dimension:
V∝L3
Therefore, if the linear dimension increases by a factor of 9, the new volume (V2) can be expressed as:
V2=93V1=729V1
The cross-sectional area (A) is proportional to the square of the linear dimension:
A∝L2
Now we can express the initial and final stress:
σ1=F1A1=m1gA1
σ2=F2A2=m2gA2
Since the density remains constant, we have:
m1=ρV1andm2=ρV2=ρ(729V1)
Thus, the new mass is:
m2=729m1
The area also changes according to the square of the linear dimension:
A2=92A1=81A1
Now substituting these into the stress equations:
σ1=m1gA1
σ2=729m1g81A1=72981⋅m1gA1=9σ1
The stress in the leg changes by a factor of 9.
The stress in the leg will change by a factor of 9.
Topper's Solved these Questions
- JEE MAINSBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINSExercise:Chemistry
Explore 1 Video
- JEE MAINBook:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINExercise:All Questions
Explore 452 Videos
- JEE MAINS 2020Book:JEE MAINS PREVIOUS YEAR ENGLISHChapter:JEE MAINS 2020Exercise:PHYSICS
Explore 250 Videos
Similar Questions
A solenoid wound over a rectangular frame. If all the linear dimensions of the frame are increased by a factor 3 and he number of turns per unit length remains the same, the self inductance increased by a factor of
View Solution(a) The potential difference applied across a given resistor is altered so that the heat produced per second increases by a factor of 9 . By what factor does the applied potential difference change?

(b) In the figure shown, an ammeter A and a resistor of 4 Ω are connected to the terminals of the source . The emf of the source is 12V having an internal resistance of 2 Ω.
Calculate the voltmeter and ammeter readings.
View Solution
Knowledge Check
A home designer will carpet n rooms with the same dimensions in a house using a specific type of carpeting. The designer charges using the expressions nClw, where n is the number of rooms, C is a constant with units of dollars per square meter. L is the length of the each room in meters, and w is the width of each room in meter. If a customer asks the designer to use a less expansive type oof carpating, which of the following factors in the expressions would change?
AnBCClDw
If the radius of the earth were increased by a factor of 2 keeping the mass constant, by what factor would its density have to be changed to keep g the same?
View SolutionThe activation energy of
H2+I2⇔2HI(g) in equilibrium for the forward reaction is 167kJmol−1 whereas for the reverse reaction is 180kJmol−1. The presence of catalyst lowers the activation energy by 80kJmol−1. Assuming that the reactions are made at 27∘C and the frequency factor for forwatd and backward reactions are 4×10−4 and 2×10−3 respectively, calculate Kc.
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Sign of work done by the camel on the load during parts of motion, accelerated motion, uniform motion and retarded motion, respectively are
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
Maximum power transmitted by the camel to load is
View SolutionQuestion 37 and 38 refer to the following information
The U.S. federal Government tracks the Consumer Price Index (CPI)- a comprehensive standard used to estimate the average price change for the typical goods and services purchased by consumers. This measure gives economics a useful way to estimate the rates of the inflation or deflation, which reflects the respective general increase or decrease of prices of goods and services in the economy. The accompanying tables summarizes the changes in the CPI for the years 2005 through 2014, which can be assumed to be the corresponding percent rates of inflation.
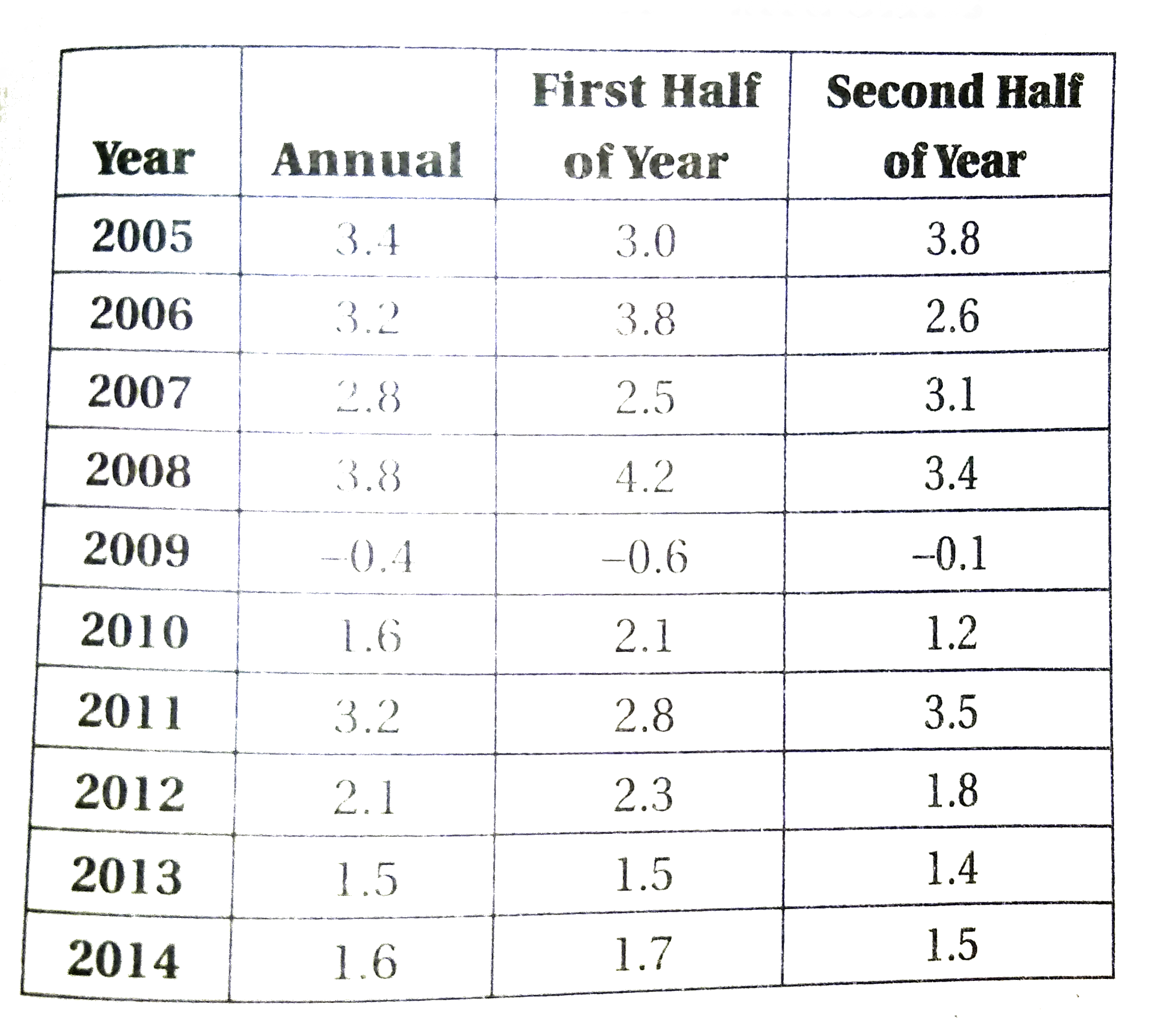
Q. At a beginning of 2015, a retired person is shopping for a retirement annunity, which is an investment policy that will give him fixed monthly payments for the rest of his life. He would like the amount of his annuity payments to more than keep up with the rate of inflation. He decides that he will choose a policy that issuse payments that increase annually at a rate of that is at least 1.5% greater than the average yearly compounded rate of inflation calculated from the period that extends from the second half of 2005 through the first half of 2008. What should be the minimum annual rate of increase in his monthly annuity payments, correct to the nearest tenth?
View SolutionRam and Ali have been fast friends since childhood. Ali neglected studies and now has no means to earn money other than a channel whereas Ram has become an engineer. Now both are working in the same factory. Ali uses camel to transport the load within the factory.
 Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
Due to low salary and degradation in health of camel, Ali becomes worried and meets his friend Ram and discusses his problems. Ram collected some data and with some assumptions concluded the following:
i. The load used in each trip is 1000kg and has friction coefficient μk=0.1 and μs=0.2.
ii. Mass of camel is 500kg.
iii. Load is accelerated for first 50m with constant acceleration, then it is pulled at a constant speed of 5ms−1 for 2km and at last stopped with constant retardation in 50m.
iv. From biological data, the rate of consumption of energy of camel can be expressed as P=18×103v+104Js−1 where P is the power and v is the velocity of the camel. After calculations on different issues, Ram suggested proper food, speed of camel, etc. to his friend. For the welfare of Ali, Ram wrote a letter to the management to increase his salary.
(Assuming that the camel exerts a horizontal force on the load):
The ratio of the energy consumed by the camel during uniform motion for the two cases when it moves with speed 5ms−1 to the case when it moves with 10ms−1
View SolutionIf each data point in a set increased by a factor of 7, does the set's standard deviation increase, decrease, or remain constant? (Assume that the set consists of different numbers.)
View Solution