Question

The activation energy of
$H_2+I_2\iff 2HI\left(g\right)$ in equilibrium for the forward reaction is $167kJmo{l}^{-1}$ whereas for the reverse reaction is $180kJmo{l}^{-1}$. The presence of catalyst lowers the activation energy by $80kJmo{l}^{-1}$. Assuming that the reactions are made at ${27}^{\circ }C$ and the frequency factor for forwatd and backward reactions are $4\times {10}^{-4}$ and $2\times {10}^{-3}$ respectively, calculate $K_c$.

Explanation

To solve the problem, we will follow these steps:

Step 1: Determine the new activation energies for both reactions
The activation energy for the forward reaction is given as 167 kJ/mol. The presence of a catalyst lowers this by 80 kJ/mol.

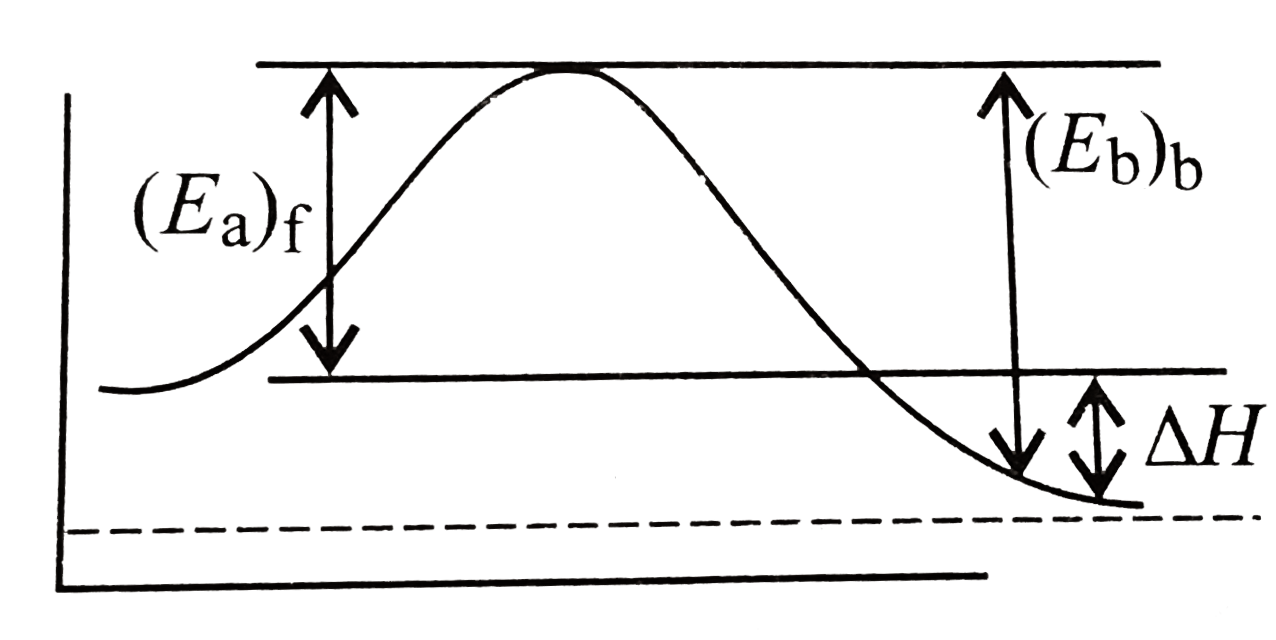
\( \text{New Activation Energy for Forward Reaction (E_a1)} = 167 \, \text{kJ/mol} - 80 \, \text{kJ/mol} = 87 \, \text{kJ/mol} \)

The activation energy for the reverse reaction is given as 180 kJ/mol. The catalyst also lowers this by 80 kJ/mol.

\( \text{New Activation Energy for Reverse Reaction (E_a2)} = 180 \, \text{kJ/mol} - 80 \, \text{kJ/mol} = 100 \, \text{kJ/mol} \)

Step 2: Write the expressions for the rate constants
The rate constants for the forward and reverse reactions can be expressed using the Arrhenius equation:

\( k_1 = A_1 e^{-\frac{E_{a1}}{RT}} \)
\( k_2 = A_2 e^{-\frac{E_{a2}}{RT}} \)

Where:
- \(k_1\) is the rate constant for the forward reaction
- \(k_2\) is the rate constant for the reverse reaction
- \(A_1\) and \(A_2\) are the frequency factors for the forward and reverse reactions respectively
- \(R\) is the universal gas constant (8.314 J/(mol·K))
- \(T\) is the temperature in Kelvin

Step 3: Calculate the equilibrium constant \(K_c\)
The equilibrium constant \(K_c\) can be expressed as:

\( K_c = \frac{k_1}{k_2} = \frac{A_1}{A_2} e^{-\frac{E_{a1}}{RT}} \cdot e^{\frac{E_{a2}}{RT}} \)

This simplifies to:

\( K_c = \frac{A_1}{A_2} e^{-\frac{E_{a1} - E_{a2}}{RT}} \)

Step 4: Substitute the values
Given:
- \(A_1 = 4 \times 10^{-4}\)
- \(A_2 = 2 \times 10^{-3}\)
- \(E_{a1} = 87 \, \text{kJ/mol} = 87000 \, \text{J/mol}\)
- \(E_{a2} = 100 \, \text{kJ/mol} = 100000 \, \text{J/mol}\)
- \(R = 8.314 \, \text{J/(mol·K)}\)
- \(T = 27^\circ C = 300 \, \text{K}\)

Now substituting these into the equation:

\( K_c = \frac{4 \times 10^{-4}}{2 \times 10^{-3}} e^{-\frac{87000 - 100000}{8.314 \times 300}} \)

Calculating the fraction:

\( \frac{4 \times 10^{-4}}{2 \times 10^{-3}} = 0.2 \)

Calculating the exponent:

\( -\frac{87000 - 100000}{8.314 \times 300} = -\frac{-13000}{2494.2} \approx 5.21 \)

Thus:

\( K_c = 0.2 e^{5.21} \)

Calculating \(e^{5.21}\):

\( e^{5.21} \approx 183.5 \)

Finally:

\( K_c \approx 0.2 \times 183.5 \approx 36.7 \)

Final Answer:
\( K_c \approx 36.8 \)