A diverging lens with magnitude of focal length is placed at a distance of from a converging lens of magnitude of focal length . A beam of parallel light falls on the diverging lens. The final image formed is.
real and 6 cm from convergent lens
real and 40 cm from convergent lens
virtual and 40 cm from convergent lens
real and 40 cm from divergent lens
The correct Answer is:D
To solve the problem step by step, we will analyze the situation involving the diverging lens and the converging lens.
Step 1: Understand the setup
We have two lenses:
- A diverging lens (concave lens) with a focal length f1=−25cm (negative because it's a diverging lens).
- A converging lens (convex lens) with a focal length f2=+20cm.
- The distance between the two lenses is d=15cm.
A beam of parallel light rays is incident on the diverging lens.
Step 2: Find the image formed by the diverging lens
Since the light rays are parallel, they can be considered to be coming from infinity. For a diverging lens, the formula for the lens is given by:
1f=1v−1u
Here, u (object distance) is taken as −∞ (since the object is at infinity), and f1=−25cm.
Using the lens formula:
1−25=1v1−1−∞
This simplifies to:
1v1=1−25
Thus,
v1=−25cm
This means the image formed by the diverging lens is virtual and located 25cm on the same side as the object (to the left of the lens).
Step 3: Determine the object distance for the converging lens
The virtual image formed by the diverging lens acts as an object for the converging lens. The distance of this virtual image from the converging lens is:
u2=d+|v1|=15cm+25cm=40cm
Since this is a real object for the converging lens, we take u2=−40cm.
Step 4: Find the image formed by the converging lens
Now we apply the lens formula for the converging lens:
1f2=1v2−1u2
Substituting the values:
120=1v2−1−40
This simplifies to:
1v2=120+140
Finding a common denominator (which is 40):
1v2=240+140=340
Thus,
v2=403≈13.33cm
Step 5: Determine the nature of the final image
Since v2 is positive, it indicates that the final image formed by the converging lens is real and located on the opposite side of the lens from the object.
Final Answer
The final image is real and located approximately 13.33cm from the converging lens.
---
We have two lenses:
- A diverging lens (concave lens) with a focal length f1=−25cm (negative because it's a diverging lens).
- A converging lens (convex lens) with a focal length f2=+20cm.
- The distance between the two lenses is d=15cm.
Since the light rays are parallel, they can be considered to be coming from infinity. For a diverging lens, the formula for the lens is given by:
The virtual image formed by the diverging lens acts as an object for the converging lens. The distance of this virtual image from the converging lens is:
Now we apply the lens formula for the converging lens:
Since v2 is positive, it indicates that the final image formed by the converging lens is real and located on the opposite side of the lens from the object.
The final image is real and located approximately 13.33cm from the converging lens.
Topper's Solved these Questions
Similar Questions
Knowledge Check
A convex lens of focal length 15 cm is placed on a plane mirror. An object is placed at 30 cm from the lens. The image is
Areal, at 30 cm in front of the mirrorBreal, at 30 cm behind the mirrorCreal, at 10 cm in front of the mirrorDvirtual, at 10 cm behind the mirror
A converging lens L1 of focal length 20 cm is separated by 8 cm from a diverging lens L2 of focal length 30cm. A parallel beam of light falls on L1 after passing through L2 is focussed at point P. Calculate V.

View SolutionA converging lens of focal length 5.0cm is placed in contact
with a diverging lens of focal length 10.0cm. Find the combined focal length of
the system.
View SolutionA converging lens of focal length 30 cm is placed in contact with another converging lens of unknown focal length, then possible value for focal length of combination is
View SolutionAn object is placed at a distance 24 cm in front of a convex lens of focal length 8 cm.
Calculate the distance of the image from the lens.
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
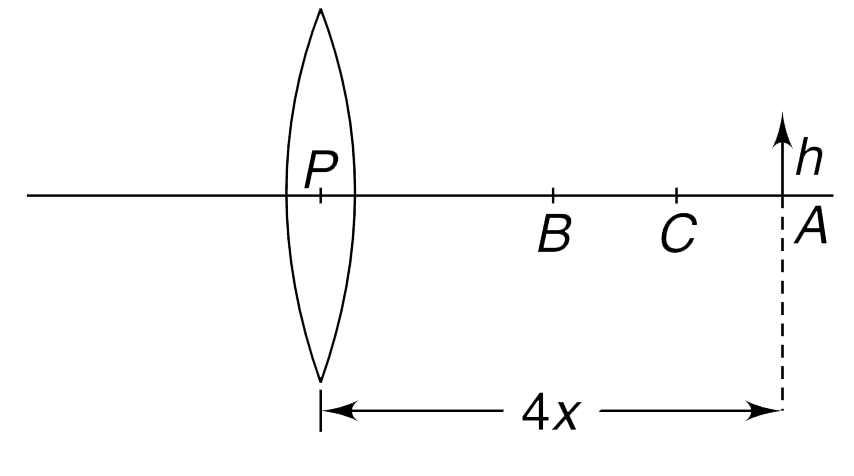
View SolutionA thin converging lens forms a real image of an object located far away from the lens. The image is formed at A at a distance 4x from the lens and height of the image is h. A thin diverging lens of focal length x is placed at B[PB=2x] and a converging lens of focal length 2x is placed at C[PC=3x]. The principal axes of all lenses coincide. Find the height of the final image formed.
View SolutionDistance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
View Solution
