Distance of an object from a concave lens of focal length 20 cm is 40 cm. Then linear magnification of the image
1
<1
<1
zero
The correct Answer is:B
To find the linear magnification of the image formed by a concave lens, we can follow these steps:
Step 1: Identify the given values
- Focal length of the concave lens (f) = -20 cm (negative because it is a concave lens)
- Object distance (u) = -40 cm (negative as per the sign convention for lenses)
Step 2: Use the lens formula
The lens formula is given by:
1v−1u=1f
Rearranging this gives:
1v=1f+1u
Step 3: Substitute the values into the lens formula
Substituting the values of f and u into the lens formula:
1v=1−20+1−40
Step 4: Find a common denominator and simplify
The common denominator for -20 and -40 is -40. Thus:
1v=−240+−140=−340
Step 5: Solve for v
Taking the reciprocal gives:
v=−403 cm
Step 6: Calculate the magnification (m)
The magnification (m) is given by the formula:
m=vu
Substituting the values of v and u:
m=−40/3−40=13
Step 7: Conclusion
The linear magnification of the image is:
m=13
This means the image is smaller than the object.
- Focal length of the concave lens (f) = -20 cm (negative because it is a concave lens)
- Object distance (u) = -40 cm (negative as per the sign convention for lenses)
The lens formula is given by:
1v−1u=1f
Rearranging this gives:
1v=1f+1u
Substituting the values of f and u into the lens formula:
1v=1−20+1−40
The common denominator for -20 and -40 is -40. Thus:
1v=−240+−140=−340
Taking the reciprocal gives:
v=−403 cm
The magnification (m) is given by the formula:
m=vu
Substituting the values of v and u:
m=−40/3−40=13
The linear magnification of the image is:
m=13
This means the image is smaller than the object.
Topper's Solved these Questions
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.510videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.620videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - RAY OPTICSEXERCISE - Checkpoint 9.320videos
RAY OPTICS
- BOOK - DC PANDEY ENGLISHCHAPTER - NUCLEIEXERCISE - C MADICAL ENTRANCES GALLERY46videos
NUCLEI
- BOOK - DC PANDEY ENGLISHCHAPTER - REFLECTION OF LIGHTEXERCISE - Subjective9videos
REFLECTION OF LIGHT
Similar Questions
An object is placed at a distance of 12 cm from a convex lens of focal length 8 cm. Find :
the position of the imageView SolutionThe magnification of an object plac ed in front of a convex lens of focal length 20 cm is +2. to obtain a magnification of -2. the object will have to be moved a distance equal to
View SolutionAn object is placed at a distance of 30 cm from a concave mirrror of
focal length 20 cm .find image distance and its magnification. Also ,drow the ray
diagram.View SolutionFind distanace of image from a convex lens of focal length
20cm if object is placed at a distance of 30cm from the lens. Also find its
magnification.View SolutionA point object O is placed at a distance of 20 cm from a convex lens of focal length 10 cm as shown in figure. At what distance x from the lens should a concave mirror of focal length 60 cm, placed so that final image coincides with the object ?
 View Solution
View SolutionA convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?
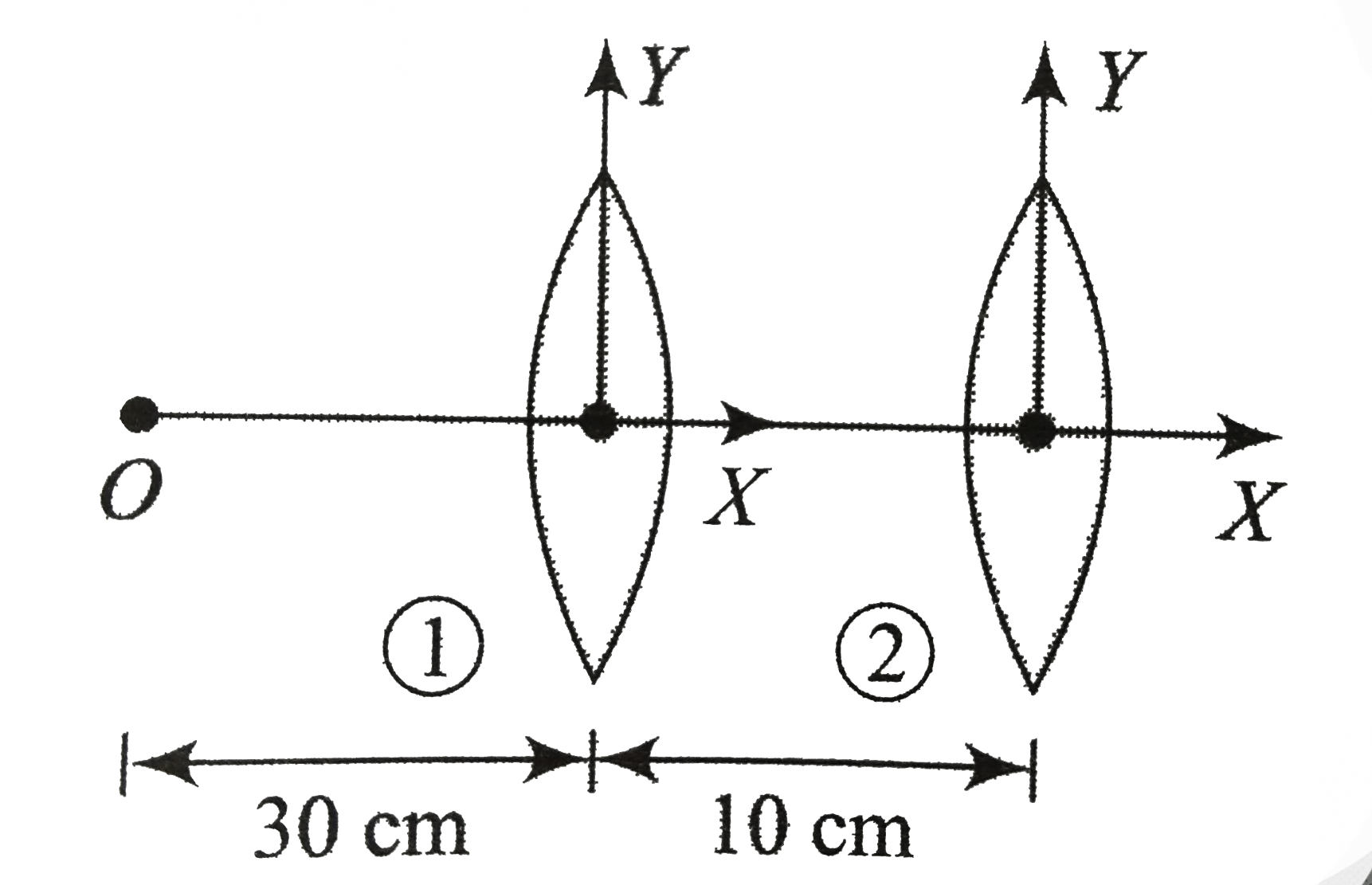 View Solution
View SolutionAn object is placed 40 cm from a concave mirror of focal length 20 cm. The image formed is
View SolutionAn object of height 2 cm is placed at a distance 20cm in front of a concave mirror of focal length 12 cm. Find the position, size and nature of the image
View SolutionAn object is kept at a distance of 15 cm from a convex lens of focal length 10 cm. Calculate the image distance and state the characteristics of the image formed.
View SolutionIn displacement method distance of object from convex lens of focal length 20 cm in one position 60 cm. Then
View Solution

