A current carrying circular loop is placed in an infinite plane if ϕi is the magnetic flux through the inner region and ϕo is magnitude of magnetic flux through the outer region, then
ϕI>ϕo
ϕI<ϕo
ϕI=−ϕo
ϕI=ϕo
The correct Answer is:C
To solve the problem, we need to analyze the magnetic flux through the inner and outer regions of a current-carrying circular loop placed in an infinite plane.
1. Understanding the Setup:
- We have a circular loop that carries a current. Let's assume the current flows in a clockwise direction.
- The magnetic field generated by the loop will have specific characteristics both inside the loop and outside of it.
2. Magnetic Field Inside the Loop:
- Inside the loop, the magnetic field lines are directed into the plane of the loop. This is represented by "cross" symbols (×).
- The strength of the magnetic field (B) inside the loop can be calculated using Ampere's Law or Biot-Savart Law, but for our purpose, we just need to know that it is directed into the loop.
3. Magnetic Field Outside the Loop:
- Outside the loop, the magnetic field lines are directed out of the plane. This is represented by "dot" symbols (•).
- The magnetic field outside the loop decreases with distance from the loop, but for an infinite plane, we can assume it extends infinitely.
4. Magnetic Flux Calculation:
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes:
Φ=B⋅A
- For the inner region (Φi), the magnetic flux is:
Φi=Binside⋅Ainner
- For the outer region (Φo), the magnetic flux is:
Φo=Boutside⋅Aouter
5. Relation Between Φi and Φo:
- The number of magnetic field lines entering the loop (inside) is equal to the number of lines exiting the loop (outside). However, since they are in opposite directions, we can establish a relationship:
Φi=−Φo
- This indicates that the magnetic flux through the inner region is equal in magnitude but opposite in direction to the magnetic flux through the outer region.
Final Answer:
Φi=−Φo
- We have a circular loop that carries a current. Let's assume the current flows in a clockwise direction.
- The magnetic field generated by the loop will have specific characteristics both inside the loop and outside of it.
- Inside the loop, the magnetic field lines are directed into the plane of the loop. This is represented by "cross" symbols (×).
- The strength of the magnetic field (B) inside the loop can be calculated using Ampere's Law or Biot-Savart Law, but for our purpose, we just need to know that it is directed into the loop.
- Outside the loop, the magnetic field lines are directed out of the plane. This is represented by "dot" symbols (•).
- The magnetic field outside the loop decreases with distance from the loop, but for an infinite plane, we can assume it extends infinitely.
- Magnetic flux (Φ) is defined as the product of the magnetic field (B) and the area (A) through which it passes:
Φ=B⋅A
- For the inner region (Φi), the magnetic flux is:
Φi=Binside⋅Ainner
- For the outer region (Φo), the magnetic flux is:
Φo=Boutside⋅Aouter
- The number of magnetic field lines entering the loop (inside) is equal to the number of lines exiting the loop (outside). However, since they are in opposite directions, we can establish a relationship:
Φi=−Φo
- This indicates that the magnetic flux through the inner region is equal in magnitude but opposite in direction to the magnetic flux through the outer region.
Φi=−Φo
Similar Questions
A closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . Which of the following option is correct

View SolutionA closed current carrying circular loop is placed on one face of a cubical box as shown in fig. The magnetic flux through area of the box contained by the loop is ϕ1 and the magnetic flux through remaining surface area of the box is ϕ2 . What is relation between them

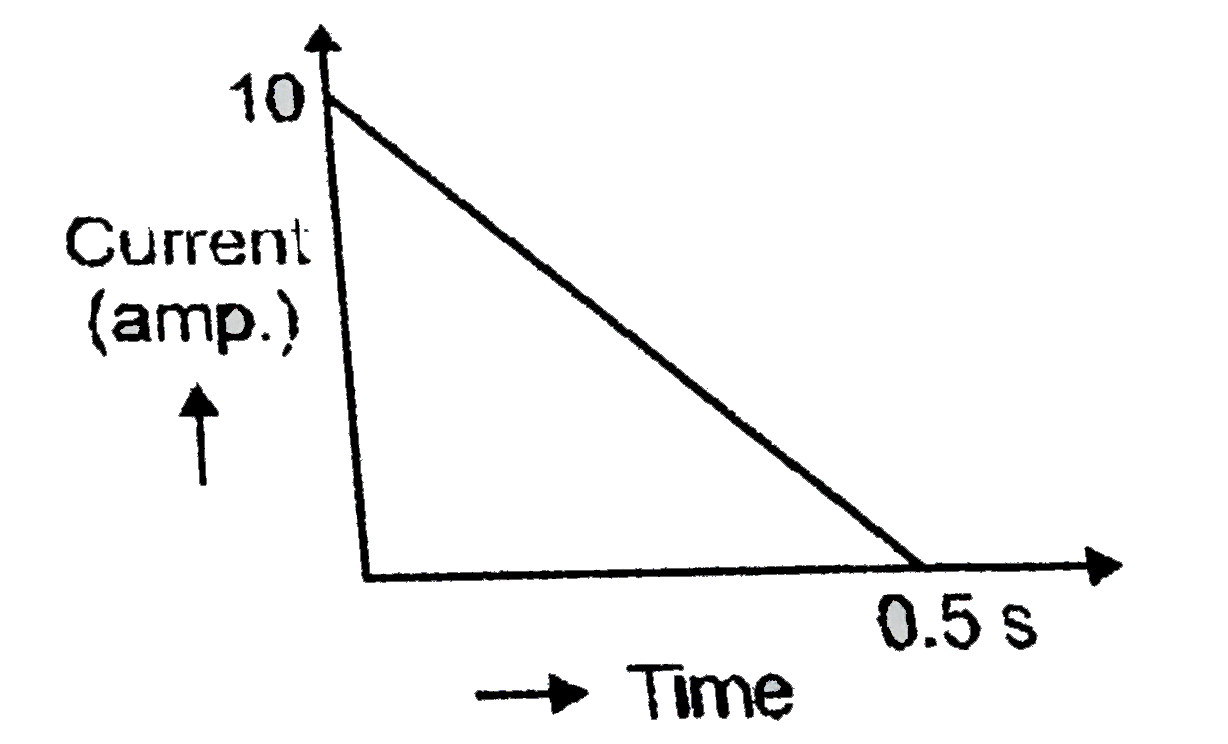
View SolutionIn a coil of resistance 100Ω , a current is induced by changing the magnetic flux through it as shown in the figure. The magnitude of change in flux through the coil is
View SolutionA current carrying circular loop is located in a uniform external magnetic field. If the loop if free to turn, what is its orientation of stable equilibrium? Show that in this orientation, the flux of the total field (external field + field produced by the loop) is maximum.
View SolutionA circular coil, carrying a constant current i s kept in the x - y plane. The magnetic flux through the entire x - y plane exluding the area of the circular coil is given by ϕ and the magetic flux through the area of the circular coil area is given by ϕ0, then
View SolutionConsider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is phi _(0) then the magnetic flux through the other circular base will be:
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionA circular loop of radius R , carrying I, lies in x−y plane with its origin . The total magnetic flux through x−y plane is
View SolutionConsider a short bar magnet forming a magnetic dipole enclosed by an imaginary co-axial cylindrical surface with circular base area. Magnet is at the middle of cylinder. If magnetic flux through one of the circular base is ϕ0 then the magnetic flux through the other circular base will be:
View SolutionThe net magnetic flux through any closed surface, kept in a magnetic field is
View Solution
